Полином в каноническом виде
Известно, что любая непрерывная на отрезке [a,b] функция f(x) может быть хорошо приближена некоторым полиномом Pn(x). Справедлива следующая Теорема (Вейерштрасса): Для любого  >0 существует полином Pn(x) степени
>0 существует полином Pn(x) степени 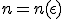 , такой, что
, такой, что 
В качестве аппроксимирующей функции выберем полином степени n в каноническом виде:
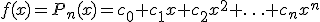
Коэффициенты полинома 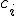 определим из условий Лагранжа
определим из условий Лагранжа 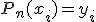 ,
,  , что с учётом предыдущего выражения даёт систему линейных алгебраических уравнений с n+1 неизвестными:
, что с учётом предыдущего выражения даёт систему линейных алгебраических уравнений с n+1 неизвестными:
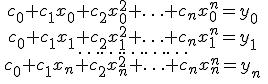
Обозначим систему таких уравнений символом (*) и перепишем её следующим образом:
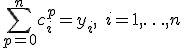
или в матричной форме: 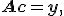 где
где  - вектор-столбец, содержащий неизвестные коэффициенты
- вектор-столбец, содержащий неизвестные коэффициенты 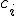 ,
,  - вектор-столбец, составленный из табличных значений функции
- вектор-столбец, составленный из табличных значений функции 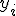 , а матрица
, а матрица  имеет вид:
имеет вид:
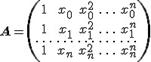
Система линейных алгебраических уравнений (*) относительно неизвестных 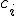 иметь единственное решение, если определитель матрицы
иметь единственное решение, если определитель матрицы  отличен от нуля.
отличен от нуля.
Определитель матрицы  называют определителем Вандермонда, его можно вычислить по следующей формуле:
называют определителем Вандермонда, его можно вычислить по следующей формуле:
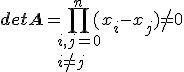
Число узлов интерполяционного полинома должно быть на единицу больше его степени. Это понятно из интуитивных соображений: через 2 точки можно провести единственную прямую, через 3 - единственную параболу и т.д. Но полином может получиться и меньшей степени. Т.е. если 3 точки лежат на одной прямой, то через них пройдёт единственный полином первой степени (но это ничему не противоречит: просто коэффициент при старшей степени равен нулю).
При достаточной простоте реализации метода он имеет существенный недостаток: число обусловленности матрицы быстро растёт с увеличением числа узлов интерполяции. Из-за плохой обусловленности матрицы рекомендуется применять другие методы интерполяции (например, интерполяция полиномами Лагранжа). При этом важно понимать, что при теоретическом применении различных методов они приводят к одинаковому результату, т.е. мы получим один и тот же полином.
Однако при практической реализации мы получим полиномы различной точности аппроксимации из-за погрешности вычислений аппаратуры.
