Модель стержня с двумя степенями свободы
Прежде чем приступить к анализу стержня со многими модами, рассмотрим модель трехзвенного шарнирно опертого стержня, который имеет две степени свободы. Этот стержень в деформированном состоянии изображен на рисунок 8.6.
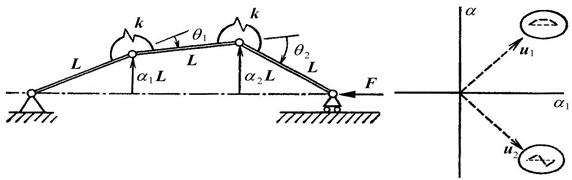
Рисунок 1.38 - Перемещения и моды в модели стержня с двумя шарнирами
Он состоит из трех стержней длиной 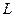 , соединенных шарнирами и образующих цепь длиной
, соединенных шарнирами и образующих цепь длиной 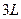 . Краевое звено цепи вращается вокруг фиксированной точки, а второе звено может свободно вращаться вокруг краевого звена. При относительном вращении стержней в точках соединений возникает сопротивление со стороны двух круговых пружин, каждая из них имеет жесткость
. Краевое звено цепи вращается вокруг фиксированной точки, а второе звено может свободно вращаться вокруг краевого звена. При относительном вращении стержней в точках соединений возникает сопротивление со стороны двух круговых пружин, каждая из них имеет жесткость 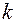 . Пружины находятся в недеформированном состоянии, когда стержни лежат на прямой линии, так что при отсутствии нагрузки стержни находятся на прямой горизонтальной линии между опорами. Система нагружается мертвой сжимающей нагрузкой
. Пружины находятся в недеформированном состоянии, когда стержни лежат на прямой линии, так что при отсутствии нагрузки стержни находятся на прямой горизонтальной линии между опорами. Система нагружается мертвой сжимающей нагрузкой 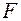 , которая по предположению сохраняет свое первоначальное значение и направление при деформировании шарниров.Система имеет две степени свободы. Вертикальные смещения точек соединения обозначаются через
, которая по предположению сохраняет свое первоначальное значение и направление при деформировании шарниров.Система имеет две степени свободы. Вертикальные смещения точек соединения обозначаются через 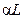 и
и 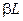 , как показано на рисунке, так что общее деформированное состояние системы может быть полностью описано безразмерными обобщенными координатами
, как показано на рисунке, так что общее деформированное состояние системы может быть полностью описано безразмерными обобщенными координатами 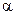 и
и 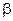 . Обе они равны нулю в недеформированном состоянии системы.
. Обе они равны нулю в недеформированном состоянии системы.
Энергия деформации, накапливаемая в двух круговых пружинах, дается формулой
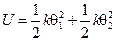 ,
,
которая может быть переписана в виде
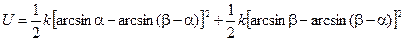 .
.
Раскладывая каждый из тригонометрических членов в ряд по 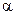 и
и 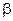 , имеем
, имеем
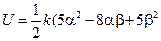 + члены высшего порядка малости).
+ члены высшего порядка малости).
Укорочение стержня, вызванное поперечным перемещением точек сопряжения, дается равенством
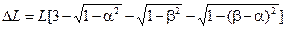 .
.
Раскладывая снова в степенной ряд, имеем 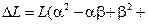 высшего порядка малости). Общая потенциальная энергия системы есть
высшего порядка малости). Общая потенциальная энергия системы есть 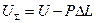 . Последний член представляет потенциальную энергию приложенной нагрузки. Вторая вариация потенциальной энергии
. Последний член представляет потенциальную энергию приложенной нагрузки. Вторая вариация потенциальной энергии 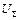 равна
равна
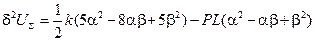 .
.
Это та самая квадратичная форма, которую нужно исследовать для изучения устойчивости прямой конфигурации. Прямая конфигурация является равновесным состоянием, поскольку в разложении потенциальной энергии отсутствуют линейные члены и первая вариация 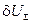 равна нулю.
равна нулю.
В рассматриваемой задаче квадратичная форма энергии деформации пружин положительно определена, так как она выведена из выражения, состоящего из суммы двух квадратов. Если имеются две квадратичные формы и одна из них положительно определена, всегда можно найти линейную замену переменных, которая одновременно приводит две формы к диагональному виду. В нашей задаче это достигается невырожденным преобразованием
 ,
,
которое имеет следующее обращение:

Чтобы понять, как расположены новые оси 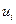 ; в
; в 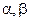 -пространстве, заметим, что
-пространстве, заметим, что 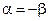 при
при 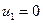 и
и 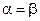 при
при 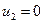 . Поэтому оси координат
. Поэтому оси координат 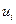 , ортогональны и повернуты на угол 45° по отношению к осям координат
, ортогональны и повернуты на угол 45° по отношению к осям координат 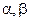 как показано на рисунке.
как показано на рисунке.
В терминах главных координат 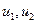 прямой подстановкой находим
прямой подстановкой находим
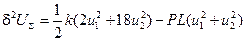 .
.
Сравнивая это выражение с суммой квадратов в стандартной форме
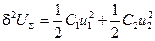 ,
,
получаем коэффициенты устойчивости
 .
.
Если приложенная нагрузка равна нулю, то прямая конфигурация устойчива, поскольку
 ,
,
и энергия имеет локальный минимум, как показано внизу справа на рисунке. Показаны энергетические поверхности для различных значений нагрузки.
По мере увеличения осевой сжимающей нагрузки 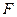 два коэффициента устойчивости уменьшаются по линейному закону до тех пор, пока
два коэффициента устойчивости уменьшаются по линейному закону до тех пор, пока 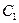 не достигнет значения, равного нулю, которое соответствует первой критической нагрузке
не достигнет значения, равного нулю, которое соответствует первой критической нагрузке 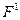 , даваемой равенством
, даваемой равенством 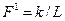 . При этой нагрузке кривизна поверхности энергии в направлении
. При этой нагрузке кривизна поверхности энергии в направлении 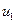 уменьшается до нуля, так что вторая вариация имеет цилиндрическую форму, показанную справа на рисунке 1.39. Говорят, что стержень теряет устойчивость по моде
уменьшается до нуля, так что вторая вариация имеет цилиндрическую форму, показанную справа на рисунке 1.39. Говорят, что стержень теряет устойчивость по моде 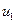 при этой критической нагрузке.
при этой критической нагрузке.
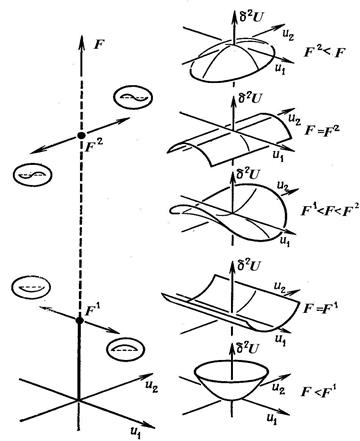
Рисунок 1.39 - Трехмерная диаграмма нагрузка-перемещение в линейной теории шарнирно опертого стержня
Если нагрузка превысила значение 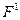 , коэффициент
, коэффициент 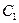 становится отрицательным, в то время как коэффициент
становится отрицательным, в то время как коэффициент 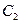 остается пока положительным. Поверхность второй вариации энергии
остается пока положительным. Поверхность второй вариации энергии 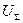 имеет теперь форму седловой точки, загибающейся вверх в направлении координаты
имеет теперь форму седловой точки, загибающейся вверх в направлении координаты 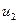 и вниз в направлении координаты
и вниз в направлении координаты 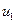 , как показано на рисунке. Прямая основная конфигурация системы теперь является неустойчивой. Можно сообщить больше информации, если сказать, что прямая конфигурация неустойчива по отношению к
, как показано на рисунке. Прямая основная конфигурация системы теперь является неустойчивой. Можно сообщить больше информации, если сказать, что прямая конфигурация неустойчива по отношению к 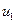 , но устойчива по отношению к
, но устойчива по отношению к 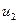 .
.
Если мы продолжаем увеличивать приложенную нагрузку 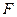 , второй коэффициент устойчивости
, второй коэффициент устойчивости 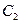 , достигнет, наконец, нулевого значения, когда нагрузка становится равной второму критическому значению
, достигнет, наконец, нулевого значения, когда нагрузка становится равной второму критическому значению 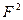 , даваемому формулой
, даваемому формулой 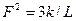 .
.
При этой второй потере устойчивости вторая вариация энергии 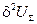 снова изображается цилиндрической поверхностью, как показано на рисунке, а для достаточно больших значений нагрузки она имеет локальный максимум.
снова изображается цилиндрической поверхностью, как показано на рисунке, а для достаточно больших значений нагрузки она имеет локальный максимум.
Можно сказать, что в модели стержня происходит потеря устойчивости по моде 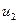 при второй критической нагрузке
при второй критической нагрузке 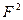 , хотя это условие не может быть достигнуто экспериментально без наложения дополнительных ограничений, исключающих более раннюю потерю устойчивости по моде
, хотя это условие не может быть достигнуто экспериментально без наложения дополнительных ограничений, исключающих более раннюю потерю устойчивости по моде 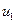 .
.
Подчеркнем, что каждая поверхность энергии, изображенная в правой части рисунка 1.40 соответствует заданному фиксированному значению приложенной нагрузки 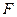 .
.
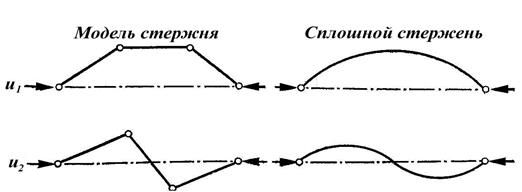
Рисунок 1.40 Моды потери устойчивости в модельной задаче о реальном сплошном стержне
Легко охарактеризовать деформации системы в терминах 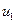
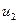 . Когда речь идет о моде
. Когда речь идет о моде 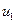 , то подразумевается деформация, которая происходит при
, то подразумевается деформация, которая происходит при 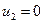 . Равенство
. Равенство 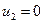 означает, согласно формулам перехода к старым переменным, что
означает, согласно формулам перехода к старым переменным, что 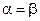 , так что мода
, так что мода 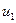 соответствует симметричной деформации, аппроксимирующей первую гармонику сплошного стержня, как показано на рисунке. Аналогично равенство
соответствует симметричной деформации, аппроксимирующей первую гармонику сплошного стержня, как показано на рисунке. Аналогично равенство 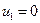 означает, что
означает, что 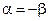 , так что мода
, так что мода 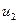 соответствует антисимметричной деформации, аппроксимирующей вторую гармонику сплошного стержня, как показано на рисунке1.40.
соответствует антисимметричной деформации, аппроксимирующей вторую гармонику сплошного стержня, как показано на рисунке1.40.
Исследование, подобное проведенному и имеющее целью определить критические нагрузки при помощи изучения второй вариации потенциальной энергии 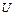 , называют линейным анализом собственных значений. Оно не добавляет новой информации о поведении системы после начального момента потери устойчивости, которое управляется слагаемыми энергии, имеющими в состоянии критического равновесия более высокий порядок малости.
, называют линейным анализом собственных значений. Оно не добавляет новой информации о поведении системы после начального момента потери устойчивости, которое управляется слагаемыми энергии, имеющими в состоянии критического равновесия более высокий порядок малости.
