I. Признаки сравнения рядов

Теорема 6.2.5. Пусть даны два положительных ряда 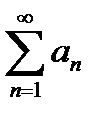(6.2.1) и 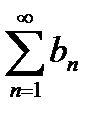(6.2.2). Если члены ряда (6.2.1) не превосходят соответствующих членов ряда (6.2.2), т. е. 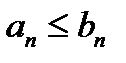(n=1, 2, 3), и ряд (6.2.2) сходится, то ряд (6.2.1) также сходится.

Теорема 6.2.6. Пусть даны два положительных ряда 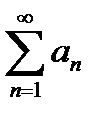(6.2.1) и 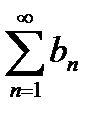(6.2.2). Если члены ряда (6.2.1) не меньше соответствующих членов ряда (6.2.2), т. е. 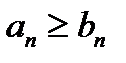(n=1, 2, 3), и ряд (6.2.2) расходится, то ряд (6.2.1) также расходится.

Пример 6.2.7.Исследовать на сходимость ряд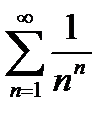

Оценим общий член данного ряда: 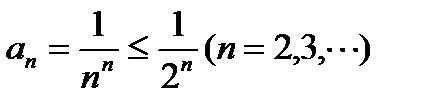. Ряд с общим членом b_n=1/2ⁿ. сходится (геометрический ряд). По теореме 6.2.6. данный ряд также сходится.

Пример 6.2.8. Исследовать на сходимость ря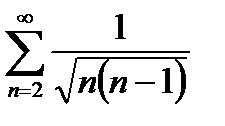

Оценим общий член данного ряда: a_n=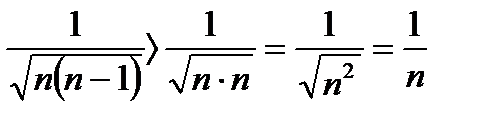

Последний ряд 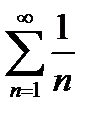расходится (как узнаете позднее, это гармонический ряд). Следовательно по теореме 6.2.6.данный ряд так же расходится.

Отметим полезное следствие из доказанных выше теорем 6.2.5. и 6.2.6.

Теорема 6.2.7. Пусть даны два положительных ряда 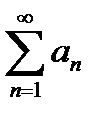(6.2.1) и 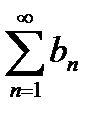(6.2.2). Если существует конечный, отличный от нуля, предел отношения общих членов этих рядов: 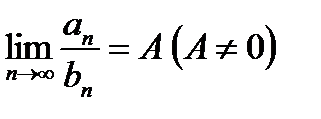, то оба ряда сходятся или расходятся одновременно.

Смысл этого следствия состоит в том, что если общий член ряда (6.2.1) и общий член ряда (6.2.2) являются бесконечно малыми (если общие члены этих рядов стремятся к нулю при 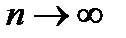, то a_n и b_n можно рассматривать как бесконечно малые) одного и тогоже порядка (при 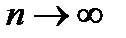)то сходимость одного из этих рядов влечет сходимость другого (а значит, и ,наоборот, расходимость одного влечет расходимость другого).

Эту теорему можно прочитать следующим образом:

Если два ряда имеют общие члены одинакового порядка малости (при 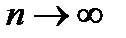), то эти ряды сходятся или расходятся одновременно.

Пример 6.2.9. .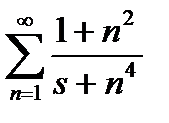

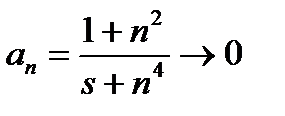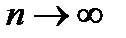при . Поэтому можно ставить вопрос о том, сходится ли данный ряд. Возьмем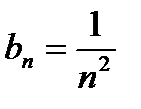

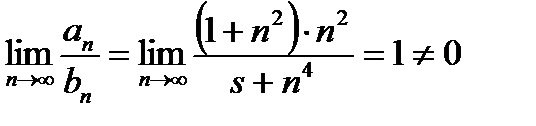
т. к. ряд 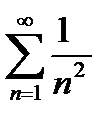сходится (что будет доказано позднее!!!),то и данный ряд сходится.

Пример 6.2.10.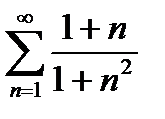

Имеем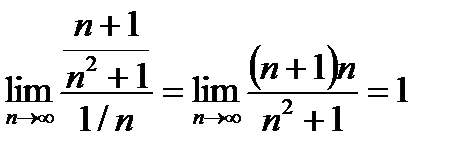

Т. к. ряд с общим членом 1/n (гармонический ряд) расходится, то и теорема (6.2.7.) будет расходится и данный ряд.

II. Признак Даламбера (в предельной форме)

Теорема 6.2.8. Если для ряда 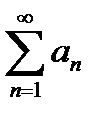с положительными членами существует конечный предел 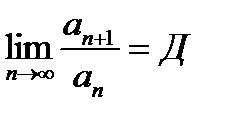(6.2.5) отношения (n+1)-го члена к n-му, то

а) при Д<1 ряд расходится, а

б) при Д>1 – расходится.

Пример 6.2.11. Выяснить, сходится ли ряд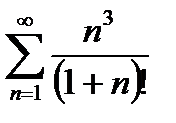

Имеем: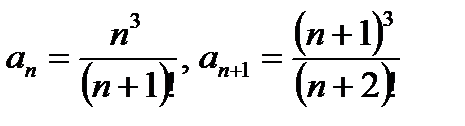

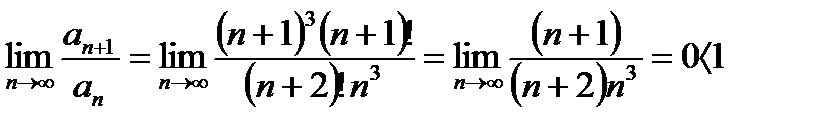
на основании признака Даламбера данный ряд сходится.

Пример 6.2.12.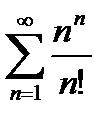

Имеем: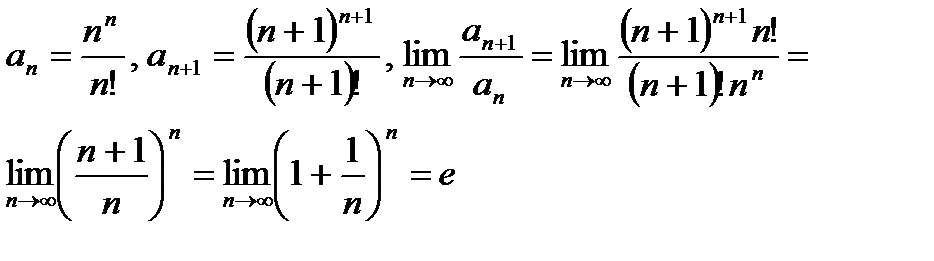

Т. к. 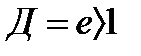, то ряд расходится.

Пример 6.2.13.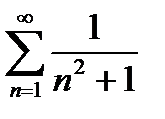

.

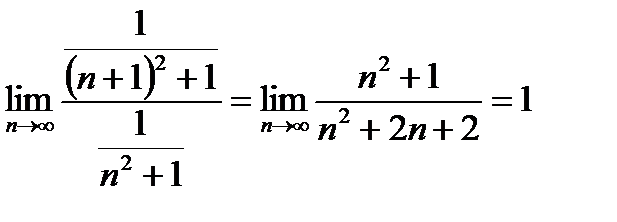Признак Даламбера ответа не дает на вопрос о сходимости данного ряда. Между тем принцип сравнения рядов решает этот вопрос: 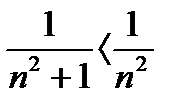при всех значениях n, а ряд с общим членом 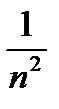сходится. Следовательно, данный ряд сходится.

Пример 6.2.14.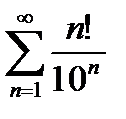

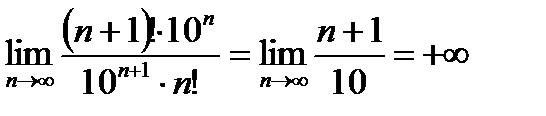. следовательно, данный ряд расходится.

III. Признак Коши (в предельной форме)

Теорема 6.2.9.. Если для положительного ряда 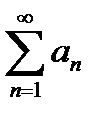существует конечный предел 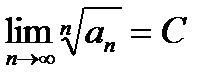, то

а) при С<1 ряд сходится, а

б) при С>1 – расходится.

Пример 6.2.15.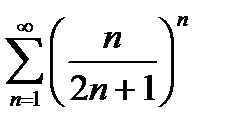

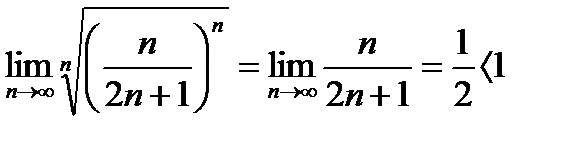- ряд сходится.

Замечание 6.2.1. Если 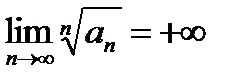, то ряд будет расходится.

Замечание 6.2.2. Если 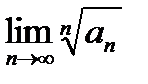1) не существует или 2) равен 1, то признак Коши, как и признак Даламбера, не дает ответа на вопрос о сходимости ряда.