Теоремы сравнения положительных рядов.

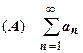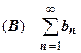18.1.3.1.1. Признак сравнения.Пусть даны два положительных ряда и , для которых, хотя бы начиная с некоторого места (при n>N), выполняется неравенство 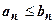. Тогда:

если сходится ряд (В), то сходится ряд (А); если расходится ряд (А), то расходится ряд (В).

Другими словами, из сходимости большего ряда следует сходимость меньшего ряда, из расходимости меньшего ряда следует расходимость большего ряда. Сразу отметим, что из расходимости большего ряда, как и из сходимости меньшего ряда, никаких выводов о сходимости второго ряда сделать нельзя.

Доказательство этого утверждения непосредственно следует из сформулированного в начале раздела признака сходимости положительных рядов: если сходится больший ряд, то последовательность его частичных сумм ограничена, следовательно, ограничена последовательность частичных сумм меньшего ряда, следовательно, меньший ряд сходится; если расходится меньший ряд, то последовательность его частичных сумм неограничена, следовательно, неограничена последовательность частичных сумм большего ряда, следовательно, больший ряд расходится.

Примеры применения признака сравнения. 1. 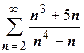. Как и в случае несобственных интегралов, применение признака сравнения требует сначала сформулировать гипотезу о том, каково поведение ряда: если мы будем доказывать, что ряд сходится, мы должны будем оценить сверху общий член ряда так, чтобы ряд из оценок сходился; если будем доказывать, что ряд расходится, мы должны оценить общий член ряда снизу так, чтобы ряд из оценок расходился. В этом примере в числителе бесконечно большая (ББ) третьего порядка по n при n 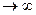, в знаменателе - четвёртого порядка, поэтому при больших 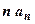~ 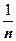. Доказываем, что ряд расходится: 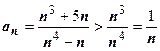(мы уменьшили числитель и увеличили знаменатель), гармонический ряд расходится, следовательно рассматриваемый ряд расходится.

2. 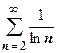. Здесь всё просто: 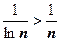, ряд расходится.

3. 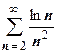. Этот пример сложнее, и в числителе, и в знаменателе стоят ББ при n 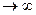функции. Пользуемся тем, что логарифм - ББ низшего порядка по сравнению с любой положительной степенью n. Так как 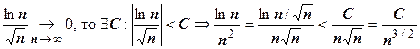. Ряд 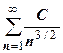- ряд Дирихле с s=3/2>1, сходится, следовательно, сходится и исходный ряд.

4. 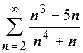. Понятно, что общий член этого ряда ведёт себя так же, как и общий член ряда, рассмотренного в первом примере, так как добавки и в числителе, и в знаменателе - ББ низших порядков по сравнению с главными членами; в то же время 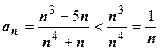, и мы не имеем права делать вывод о расходимости ряда исходя из расходимости гармонического ряда. Такие примеры легко решаются с помощью предельного признака сравнения.

18.1.3.1.2. Предельная форма признака сравнения. Если существует конечный 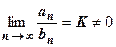, то ряды (А) и (В) сходятся или расходятся одновременно.

Доказательство. По определению предела для 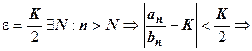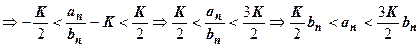. Последнего неравенства достаточно для доказательства всех утверждений теоремы. 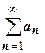сходится 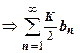сх-ся 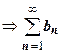сх-ся. остальные случаи схематично: (А) расх-ся 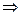(3К/2 B) расх-ся 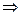(B) расх-ся; (B) сх-ся 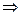(3К/2 B) сх-ся 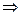(A) сх-ся; (B) расх-ся 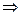(К/2 B) расх-ся 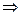(A) расх-ся.

Примеры применения предельного признака сравнения. 1. 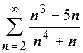. Теперь этот пример решается просто. Будем считать исходный ряд рядом (А), возьмём 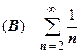; 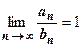, (В) расх-ся 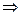(А) расх-ся.

Мы можем значительно расширить круг задач, которые способны решить, за счёт таблицы эквивалентных бесконечно малых:

2. 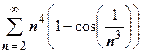. Так как 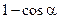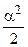^~ при , ^~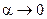

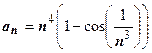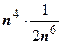^~ , поэтому 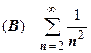, , 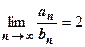(В) сх-ся 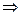(А) сх-ся.

3. 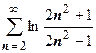. Аргумент логарифма 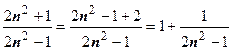, так как 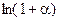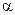^~ при 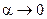, 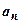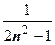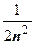^{~ ~} , поэтому 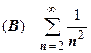, , 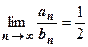(В) сх-ся 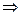(А) сх-ся и т.д.

Сравнение положительного ряда с рядом Дирихле позволяет сформулировать такое правило: если при 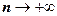функция 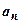- бесконечно малая порядка малости выше первого по сравнению с 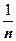, то ряд 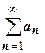сходится; если 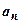не является бесконечно малой или имеет порядок малости единица или ниже, то ряд расходится. Примеры:

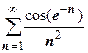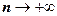
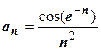4. . При эквивалентна функции 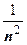, поэтому ряд сходится.

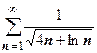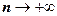
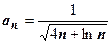5. . При эквивалентна функции 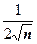, поэтому ряд расходится.

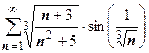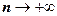
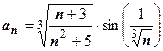6. . При эквивалентна функции 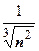, поэтому ряд расходится.

В этих примерах мы, в основном, сравнивали ряд с рядом Дирихле. Сравнение с геометрической прогрессией (в том смысле, чтобы извлечь из общего члена аналог знаменателя прогрессии q), даёт признаки Коши и Даламбера.

18.1.3.2.Признак сходимости Коши (радикальный). Пусть для положительного ряда существует 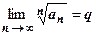. Тогда

если q<1, то ряд сходится,

если q >1, то ряд расходится,

если q=1, то ряд может и сходиться, и расходиться.

Доказательство. 1. Пусть 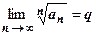<1. Возьмём . .

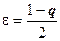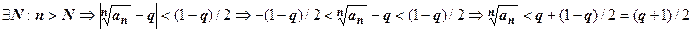Если q<1, то число 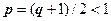. Итак, при 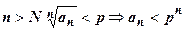. Прогрессия 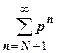сходится, так как р<1, поэтому 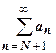сходится, поэтому 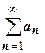сходится.

2. Пусть 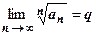>1. Возьмём . .

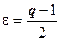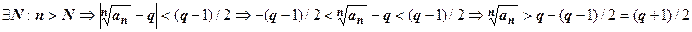Если q>1, то число 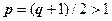. Итак, при 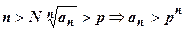. Прогрессия 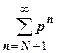расходится, так как р>1, поэтому 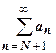расходится, поэтому 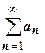расходится.

3. Чтобы убедиться, что в случае q =1 мы не можем сделать вывод ни о сходимости, ни о расходимости ряда, рассмотрим два примера: 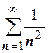и 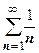. Первый из этих рядов сходится, второй расходится, но в обоих случаях q=1, например .

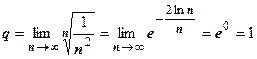Примерыприменения признака Коши. 1. 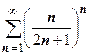. 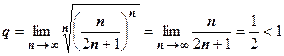, поэтому ряд сходится.

2. 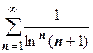. 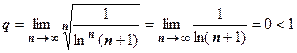, поэтому ряд сходится.

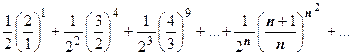
3. 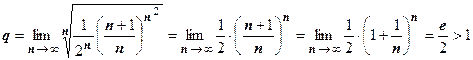, поэтому ряд расходится.

18.1.3.3.Признак сходимости Даламбера. Пусть для положительного ряда существует 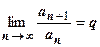. Тогда

если q<1, то ряд сходится,

если q >1, то ряд расходится,

если q=1, то ряд может и сходиться, и расходиться.

Доказательство. 1. Пусть 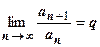<1. Возьмём 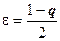. . 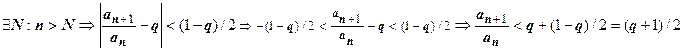Если q<1, то число 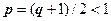. Итак, при 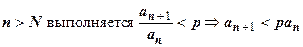. Выпишем это неравенство для 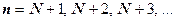: 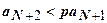, , 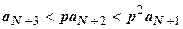, 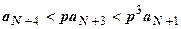… , 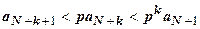. Все члены ряда, начиная с N+2-го, меньше членов сходящейся геометрической прогрессии, поэтому 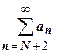сходится, поэтому 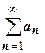сходится.

2. Пусть 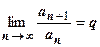>1. Возьмём . .

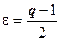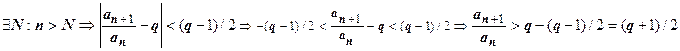Если q>1, то число 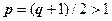. Итак, при 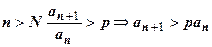. Выпишем это неравенство для 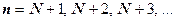: 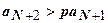, , 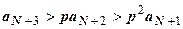, 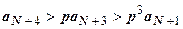… , 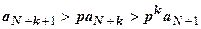. Все члены ряда, начиная с N+2-го, больше членов расходящейся геометрической прогрессии, поэтому 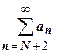расходится, поэтому 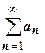расходится.

3. Для рядов 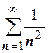и 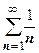мы опять получим q =1. Первый из этих рядов сходится, второй расходится, но для обоих q=1, т.е. в этом случае вопрос о сходимости ряда действительно остаётся открытым.

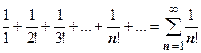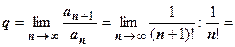
Признак Даламбера хорошо работает, если общий член ряда содержит факториалы. Примеры. 1. ; 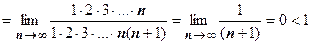, поэтому ряд сходится.

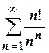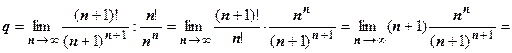
2. ; 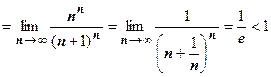, поэтому ряд сходится.

3. 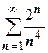; 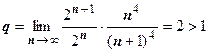, поэтому ряд расходится.

4. 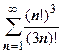. Прежде чем вычислять q, разберёмся, на сколько сомножителей в выражении 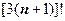больше, чем в (3n)!: 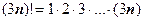; 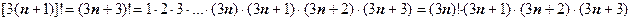, поэтому 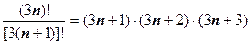; 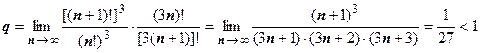, поэтому ряд сходится.

18.1.3.4. Интегральный признак Коши. Радикальный признак Коши и признак Даламбера могут установить факт сходимости или расходимости для широкого круга рядов, но для рядов, общие члены которых содержат степенные выражения, они дают q =1, и вопрос о сходимости остаётся открытым. Мы это видели на примере рядов 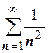и 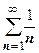. То же мы получим для рядов вида 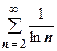, 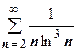и т.д. Для некоторых из этих рядов оказывается результативным интегральный признак Коши.

Теорема.Пусть члены положительного числового ряда 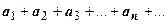являются значениями непрерывной монотонно убывающей неотрицательной функции при натуральных значениях аргумента: 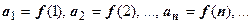Тогда ряд 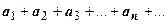и несобственный интеграл 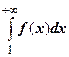сходятся или расходятся одновременно.

Доказательство. Обозначим 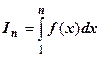. Согдасно геометрическому смыслу определённого интеграла, это площадь криволинейной трапеции под кривой у= над отрезком [1,n]. Частичная сумма 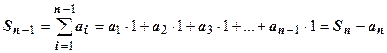- площадь ступенчатой фигуры, расположенной над криволинейной трапецией (сплошная верхняя граница на рисунке). Сумма 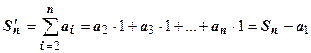- площадь ступенчатой фигуры, расположенной под криволинейной трапецией (пунктирная верхняя граница на рисунке). Очевидно, 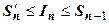, или 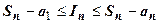. Из этого неравенства, в котором 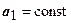, , 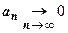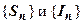- монотонно возрастающие с ростом n последовательности, и следуют все утверждения теоремы. Например:

1. Пусть интеграл 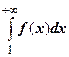сходится. Это означает, что существует конечный 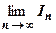, т.е. последовательность 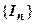ограничена сверху последовательность 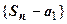ограничена сверху 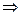существует конечный 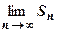, т.е. ряд 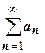сходится.

2. Пусть интеграл 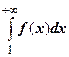расходится. Это означает, что 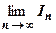бесконечен, т.е. последовательность 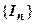неограничена сверху последовательность 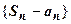неограничена сверху 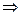не существует конечного 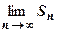, т.е. ряд 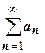расходится.

3, 4. Случаи, когда сходится и расходится ряд, рассмотреть самостоятельно.

Теперь мы можем дать простое доказательство того, что ряд Дирихле

сходится при s>1 и расходится в остальных случаях. Функция 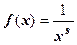удовлетворяет условиям теоремы: непрерывна, монотонно убывает, 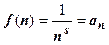. Интеграл 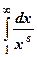сходится, как мы знаем, при s>1 и расходится при других значениях s, что и требовалось доказать.

Другие примеры применения интегрального признака Коши:

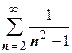. Здесь 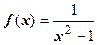удовлетворяет условиям теоремы; интеграл 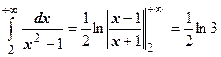сходится, поэтому ряд сходится.

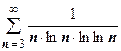. Здесь 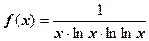удовлетворяет условиям теоремы; интеграл 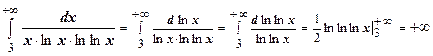расходится, поэтому ряд расходится.

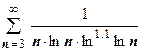. Здесь 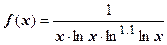удовлетворяет условиям теоремы; интеграл 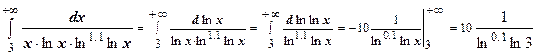сходится, поэтому ряд сходится.

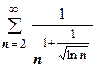. Здесь установить, что функция 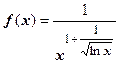удовлетворяет условиям теоремы, немного сложнее. То, что 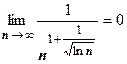, очевидно (например, 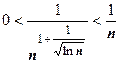и теорема о пределе промежуточной функции). Для доказательства того, что функция монотонно убывает, найдём её производную; при этом придётся воспользоваться логарифмическим дифференцированием: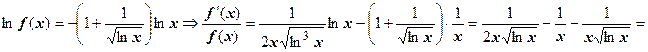 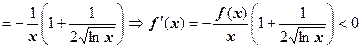, т.е. монотонное убывание действительно имеет место. Вычисляем интеграл: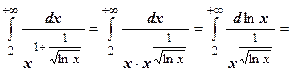 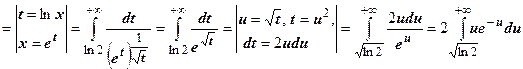, и интегрированием по частям убеждаемся, что интеграл сходится, следовательно, ряд сходится.

На этом мы заканчиваем изучение рядов с положительными членами; в следующем разделе будут рассмотрены ряды, члены которых могут иметь произвольные знаки. Для положительных рядов мы изучили целую кучу признаков сходимости, от простого признака сравнения до интегрального признака Коши. На самом деле это малая часть существующих методов исследования сходимости рядов, имеются значительно более тонкие признаки. Все эти признаки, по существу, базируются на признаке сравнения: если ряд сходится, то все ряды, члены которых не больше членов этого эталонного ряда, сходятся, и наоборот, если эталонный ряд расходится, то расходятся все ряды, члены которого не меньше членов этого ряда. В роли эталонного ряда может браться несобственный интеграл, но это несущественно. Естественен вопрос: зачем такие излишества, нельзя ли найти универсальный ряд, с помощью которого удастся сформулировать универсальный признак сходимости? Можно показать, что такого универсального ряда не существует: для любого сходящегося ряда можно построить ряд, который сходится ещё медленнее (в том смысле, что его остаток есть бесконечно малая низшего порядка по сравнению с остатком эталонного ряда); для любого расходящегося ряда можно построить ряд, который расходится медленнее (т.е. его частичные суммы есть бесконечно большие низшего порядка по сравнению с частичными суммами расходящегося эталонного ряда ).

18.1.4. Знакопеременные ряды.Так мы будем называть ряды, которые содержат бесконечные множества как положительных, так и отрицательных членов. Естественно попытаться свести исследование сходимости таких рядов к исследованию сходимости рядов с положительными членами, для которых имеются рассмотренные выше тонкие признаки сходимости, поэтому введём понятие абсолютной сходимости.

18.1.4.1. Абсолютная и условная сходимость числовых рядов. Рассмотрим, вместе с рядом 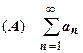, ряд, составленный из модулей членов ряда (А): 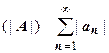. Докажем теорему: если сходится ряд (|A|), то сходится исходный ряд (А).

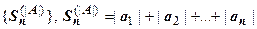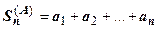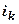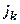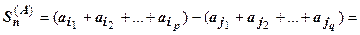
Доказательство. Пусть сходится ряд (|A|). Это – сходящийся ряд, поэтому множество его частичных сумм , ограничено. В частичной сумме исходного ряда отделим множества неотрицательных и отрицательных членов; неотрицательным членам припишем индекс , у отрицательных членов вынесем знак за скобку и их модулям припишем индекс : 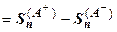; здесь символом 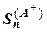обозначена сумма входящих в 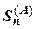положительных членов, 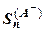обозначает сумму модулей входящих в 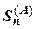отрицательных членов, 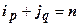. Итак,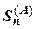 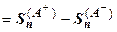. Очевидно, что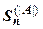 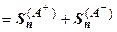. 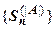- ограниченное множество, поэтому 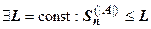. Но 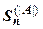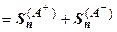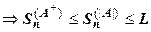, 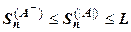. Суммы 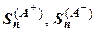тоже возрастают с ростом n и ограничены сверху, поэтому существуют конечные пределы 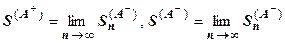. Но 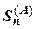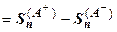, поэтому существует конечный предел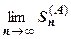 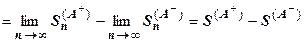, т.е. исходный ряд (А) сходится, что и требовалось доказать.

Определение. Ряд 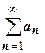называется абсолютно сходящимся, если сходится ряд 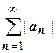абсолютных величин его членов. Если ряд 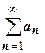сходится, а ряд 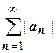расходится, то ряд 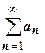называется условно сходящимся.

Доказанная теорема сводит исследование некоторых знакопеременных рядов к положительным рядам. Для знакопеременных рядов определённой структуры - знакочередующихся рядов - также существует достаточный признак сходимости.

Знакочередующиеся ряды.

Определение.Знакочередующимися называются ряды, члены которых поочерёдно то неотрицательны, то отрицательны.

Согласно этому определению, структура знакопеременных рядов такова:

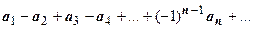, или 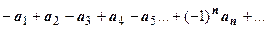, где все 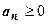. Мы будем рассматривать первую из этих форм; вторая сводится к первой выносом знака за сумму.

Достаточный признак сходимости знакочередующегося ряда (признак Лейбница).Если

1. Последовательность, составленная из модулей членов знакочередующегося ряда, монотонно убывает, т.е. ;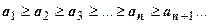

2. Выполняется необходимый признак сходимости ряда, т.е. ,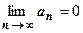

то ряд сходится. Его сумма по абсолютной величине не превосходит абсолютную величину первого члена.

Доказательство. Рассмотрим последовательность чётных частичных сумм 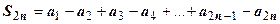ряда. Представим эту сумму в виде 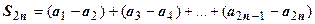. Из первого условия теоремы следует, что суммы в круглых скобках неотрицательны, поэтому последовательность 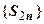монотонно возрастает с ростом n. С другой стороны, 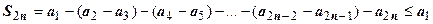, т.е. эта последовательность ограничена сверху величиной 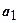. Следовательно 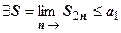. Но для нечётных сумм 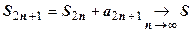, так как по второму условию теоремы 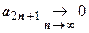. Таким образом, частичные суммы имеют предел независимо от их четности или нечётности, т.е. ряд сходится, и его сумма 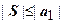. Знак суммы совпадает со знаком первого члена.

С помощью признака Лейбница доказывается сходимость рядов 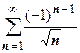, 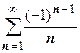. 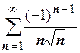, 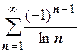и т.д. Третий из этих рядов сходится абсолютно ( 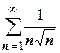сходится), остальные - условно (ряды из модулей членов расходятся). Естественно, существуют знакочередующиеся ряды, для которых условия теоремы Лейбница могут не выполняться; если не выполняется второе условие - необходимый признак сходимости - то ряд заведомо расходится; если не выполняется первое условие, то задача должна решаться с помощью других соображений. Рассмотрим, например, ряд 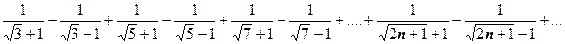Понятно, что первое условие теоремы Лейбница не выполняется (например, 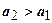), поэтому эта теорема неприменима и требуется изобрести индивидуальный способ решения этой задачи. Сгруппируем члены попарно: 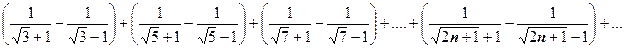Сумма в скобке 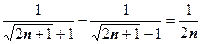, поэтому последний ряд (со скобками) расходится. Последовательность чётных частичных сумм неограничена, поэтому исходный ряд расходится.

У теоремы Лейбница есть исключительно важный для приложений вывод - вывод о том, что сумма знакочередующегося ряда (или, как говорят, ряда лейбницевского типа) по модулю не больше модуля первого члена: 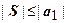. На нашем уровне нас интересует, в основном, вопрос о сходимости ряда, но при решении практических задач вслед за вопросом о сходимости ряда встаёт вопрос о нахождении его суммы. Основной метод суммирования рядов - вычисление его частичной суммы с количеством слагаемых, обеспечивающим заданную точность. Рассмотрим два примера: найти суммы рядов 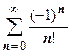и 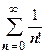с погрешностью, не превышающей 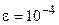. Оба ряда сходятся (пример 1 раздела 18.1.3.3.Признак сходимости Даламбера). Основная проблема здесь - найти, какое количество n слагаемых надо взять, чтобы частичная сумма 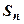отличалась от суммы ряда S не более, чем на 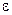. Так как 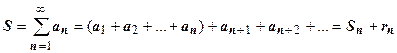, где 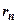- остаток ряда после n-го члена, и мы хотим принять 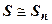, то должно быть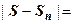 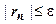. И здесь выясняется различие в технике оценки остатка для Лейбницевских рядов с одной стороны и произвольных рядов с другой стороны. Остаток знакочередующегося ряда - тоже знакочередующийся ряд, поэтому он подчиняется выводу теоремы Лейбница: 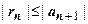. Другими словами, остаток знакочередующегося ряда по модулю не превосходит первый свой член (или первый отброшенный член ряда). Поэтому для первого из рассматриваемых рядов условие 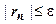сводится к 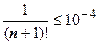. Подбором убеждаемся, что первое значение n, для которого это условие выполняется, есть n =7 (7!=5040, 8!=40320), поэтому для нахождения суммы ряда 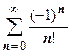с погрешностью, не превышающей величину 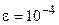, достаточно взять 7 слагаемых: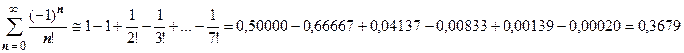

(при вычислениях с точностью до 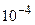в промежуточных выкладках необходимо удерживать не меньше, чем 5 знаков после запятой. Дальше мы поймём, что вычислено значение 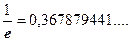с четырьмя верными цифрами после запятой).

Переходим ко второму ряду. Это знакопостоянный ряд, поэтому единственное, что мы можем сделать - напрямую оценить остаток ряда 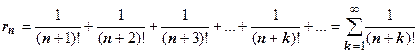. Пока единственный ряд, для которого мы знаем выражение суммы - геометрическая прогрессия 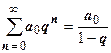, поэтому надо в той или иной форме свести остаток к геометрической прогрессии. В данном случае это сделать просто: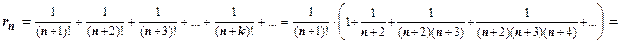 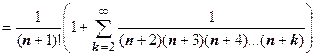. Для каждого из слагаемых в круглой скобке верна оценка 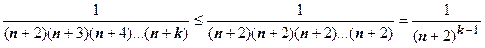, поэтому 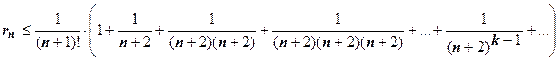. Ряд в круглых скобках - геометрическая прогрессия со знаменателем 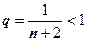, его сумма равна 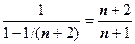, следовательно, 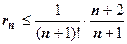. Теперь надо найти такое n, что 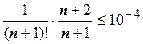. Перебором различных значений n убеждаемся, что и в этом случае можно взять n =7 (выражение 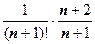равно 0,0002268 при n = 6 и 0,000028 при n = 8. Итак, 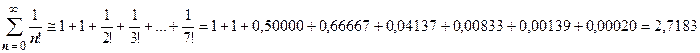. Это значение числа е с четырьмя верными цифрами после запятой.

18.1.5. Свойства сходящихся рядов и их сумм. В разделе 18.2. Свойства сходящихся рядов мы сформулировали и доказали некоторые из этих свойств. Напомним:

18.1.5.1. Необходимый признак сходимости ряда. Общий член сходящегося ряда стремится к нулю: .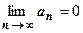

18.1.5.2. Если сходится ряд, то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.

18.1.5.3. Если ряд сходится, то сумма его остатка после n-го члена стремится к нулю при .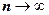

18.1.5.4. Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.

18.1.5.5.Два сходящихся ряда можно почленно складывать и вычитать, полученный ряд также сходится, и его сумма равна, соответственно, сумме или разности исходных рядов.

Сформулируем ещё несколько свойств сходящихся рядов.

18.1.5.6. Сочетательное свойство сходящегося ряда.Если члены сходящегося ряда 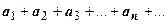сгруппировать произвольным образом: 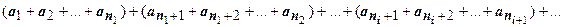(здесь 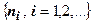- строго возрастающая последовательность натуральных чисел), и составить новый ряд из сумм членов в каждой паре круглых скобок, то этот новый ряд тоже будет сходиться, и его сумма будет равна сумме исходного ряда.

Доказательство.Последовательность частичных сумм нового ряда является подпоследовательностью 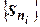последовательности частичных сумм 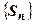исходного ряда и сходится к той же сумме.

Все сформулированные свойства полностью аналогичны свойствам конечных сумм, хотя и здесь есть свои тонкости. Так, для конечных сумм можно не только расставлять, но и раскрывать скобки; при этом сумма не меняется. Для рядов это неверно. Пример: если в сходящемся ряде 0+0+0+…+0+… = (1-1) + (1-1)+(1-1)+….+(1-1)+… раскрыть скобки, то получится расходящийся ряд 1-1+1-1+1-1+… . Конечно, если после раскрытия скобок получится сходящийся ряд, его сумма будет такой же, как и у ряда со скобками; это следует из доказанного сочетательного свойства.

18.1.5.7. Переместительное свойство ряда. Ещё больше отличаются поведение конечных сумм и рядов по отношению к переместительному свойству, т.е. к перестановке слагаемых. Если для конечных сумм результат не зависит от порядка слагаемых, то для рядов это не всегда верно. Ряд 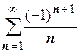условно сходится, обозначим его сумму S: 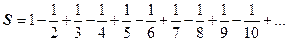. Умножим этот ряд на 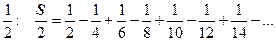. Запишем этот ряд так: 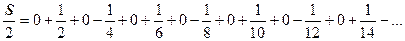Почленно сложим этот ряд и ряд S:

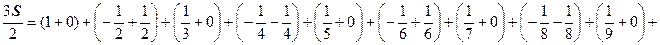
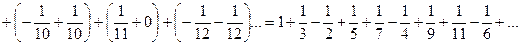. Итак, 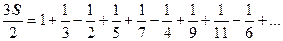. Этот ряд отличается от ряда S только порядком слагаемых, однако его сумма в полтора раза больше.

На перестановку членов резко по разному реагируют абсолютно и условно сходящиеся ряды.