Общий достаточный признак сходимости знакопеременных рядов. Абсолютная и условная сходимости числовых рядов. Свойства абсолютно сходящихся рядов
Пусть дан знакопеременный ряд
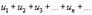 .
.
Если сходится ряд
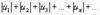 ,
,
составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.
Абсолютная и условная сходимость
Ряд 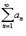 называется абсолютно сходящимся, если ряд
называется абсолютно сходящимся, если ряд 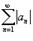 также сходится.
также сходится.
Если ряд 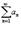 сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.
сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.
Ряд 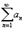 называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Свойства:
1. Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд.(теорема Дирихле)
2. Абсолютно сходящиеся ряды с суммами 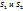 , можно пчленно складывать(вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна
, можно пчленно складывать(вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна 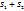 ,(или соотв-о
,(или соотв-о 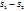 ,)
,)
3. Под произведением двух рядов 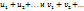 понимают ряд вида
понимают ряд вида 
Произведение двух абсолютно сходящихся рядов с суммами 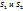 есть абсолютно сходящийся ряд, сумма кот.равна
есть абсолютно сходящийся ряд, сумма кот.равна 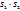
Функциональные ряды. Основные понятия
Ряд 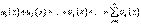 , члены которого являются функциями от переменной
, члены которого являются функциями от переменной  , называется функциональным.
, называется функциональным.
При различных значениях 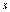 из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.
из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.
Если ряд сходится то 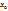 -наз. точкой сходимости
-наз. точкой сходимости
Если расходится то 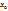 -наз. Точкой расходимости.
-наз. Точкой расходимости.
Совокупность числовых значений аргумента 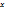 , при которых функциональный ряд сходится, наз. Его областью сходимости.
, при которых функциональный ряд сходится, наз. Его областью сходимости.
Очевидно, что в области сходимости функционального ряда его сумма является функцией от 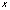 . Будем ее обозначать
. Будем ее обозначать 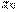 .
.
