Визначений та невласний інтеграли
1. Означення визначеного інтеграла, його геометричний і фізичний зміст, умови існування. Обчислення визначених інтегралів за формулою Ньютона – Лейбніця. Заміна змінної і інтегрування частинами у визначеному інтегралі. Обчислення площі плоскої фігури.
2. Невласні інтеграли першого роду (з нескінченними межами інтегрування)
та невласні інтеграли другого роду (від функцій, необмежених на скінченому проміжку).
ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ
1. Задачі, що приводять до звичайних диференціальних рівнянь першого порядку. Основні поняття і означення.
2. Диференціальні рівняння першого порядку: з відокремлюваними змінними, однорідні, лінійні.
3. Диференціальні рівняння другого порядку: лінійні однорідні та лінійні неоднорідні (зі спеціальною правою частиною) зі сталими коефіцієнтами.
ЧИСЛОВІ РЯДИ
1. Числові ряди: основні поняття і означення. Необхідна умова збіжності. Основні властивості збіжних рядів. Дослідження збіжності числових рядів з додатними членами.
2. Достатні умови (ознаки) збіжності додатних числових рядів:ознака порівняння, ознака Даламбера, радикальна ознака Коші.
3. Знакопочережні ряди. Ознака Лейбніця.
ТЕОРІЯ ЙМОВІРНОСТЕЙ
Елементи комбінаторикитапоняття ймовірності події, обчислення:
формули комбінаторики-розміщення, перестановки, сполучення; класична формула теорії ймовірностей; обчислення ймовірностей випадкових подій.
ДОВІДКОВИЙ МАТЕРІАЛ
ВИЗНАЧЕНИЙ ІНТЕГРАЛ
Формула Ньютона - Лейбніця для обчислення визначених інтегралів
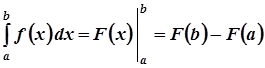 .
.
Спосіб підстановки у визначених інтегралах
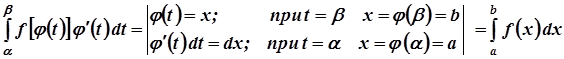 .
.
Спосіб інтегрування за частинами у визначених інтегралах
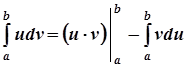 .
.
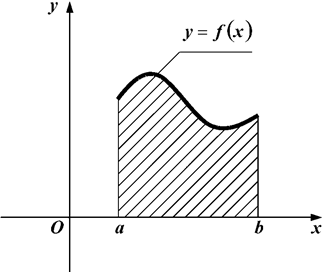 Обчислення площі плоскої фігури.
Обчислення площі плоскої фігури.
а) криволінійна трапеція:
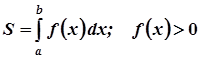 ,
,
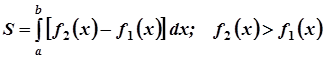 .
.
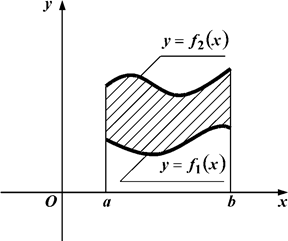
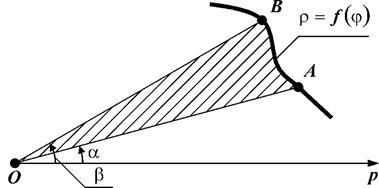
б) криволінійний сектор:
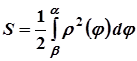 ,
,
Невласні інтеграли з нескінченними границями
а) невласні інтеграли з нескінченними границями
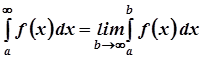 .
.
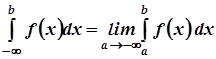 .
.
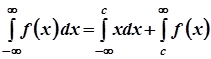 , де
, де 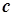 –довільне значення,
–довільне значення, 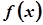 – всюди неперервна функція.
– всюди неперервна функція.
Якщо границя такого інтегралу є кінцевою, то такий інтеграл називається збіжним; у разі, коли інтеграл прямує до 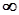 , його називають розбіжним.
, його називають розбіжним.
б) невласні інтеграли від розривних функцій
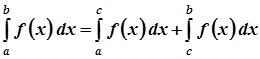 ,
,
де 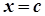 – точка розриву функції, де
– точка розриву функції, де
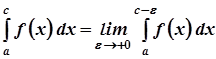 .
.
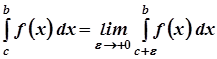 .
.
ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ
Диференціальним рівнянням (надалі, Д.Р.) називається рівняння, що містить похідні або диференціали невідомої функції. Найбільший порядок похідних називається порядком диференціального рівняння.
Д.Р. вигляду N1(y)M1(x)dx+M2(x)N2(y)dy=0 називаються Д.Р. з відокремленими змінними.
Д.Р. називається однорідним, якщо його можна подати у вигляді: 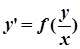 .
.
Воно за допомогою заміни змінної 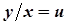 Þ
Þ 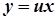 зводиться до Д.Р. з відокремлюваними змінними.
зводиться до Д.Р. з відокремлюваними змінними.
Д.Р. виду y’+P(x)y=Q(x) називається лінійним Д.Р. Його розв’язок розшукується у вигляді 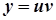 .
.
Приклад 1. Розв’язати задачу Коші (знайти загальний розв’язок диференційного рівняння і частинний розв’язок при заданих початкових умовах):

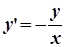 ,
, 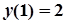 .
.
Розв’язання. Запишемо рівняння у диференціалах:
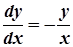 .
.
Дане рівняння є рівнянням першого порядку з відокремлюваними змінними (тобто може бути зведене до вигляду, коли з одного боку знака рівності присутня тільки залежна змінна y, а з іншого – тільки незалежна змінна x, таку рівність можна про інтегрувати і отримати загальний інтеграл рівняння).
Виконаємо відокремлення змінних, для чого домножимо рівняння на 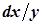 , в результаті отримаємо рівняння з відокремленими змінними
, в результаті отримаємо рівняння з відокремленими змінними
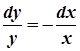 .
.
Проінтегруємо отримане рівняння:
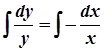 ,
,
і отримаємо
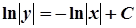 .
.
Це – загальний інтеграл рівняння у неявному вигляді. Звідси:
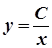 .
.
Частинний розв’язок знаходимо за допомогою початкової умови , підставляючи її о загального розв’язку:
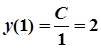 ; С=2.
; С=2.
Тоді частинним розв’язком диференційного рівняння є
.
Приклад 2. Знайти частинний розв’язок диференційного рівняння при заданих початкових умовах

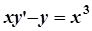 ,
, 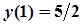 .
.
Розв’язання. Дане рівняння є лінійним диференційним рівнянням першого порядку.
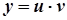 ;
; 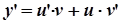 ;
;
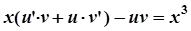 ,
,
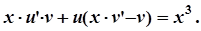
Накладемо на функцію v умову, щоб вираз у дужках дорівнював нулю, тобто
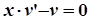 ,
,
і знайдемо функцію v з отриманого диференційного рівняння.
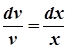
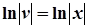 ,
, 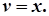
Тепер функцію u знаходимо з рівняння
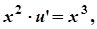
що утворюється в результаті підстановки v = x до початкового рівняння:
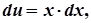
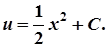
Оскільки y = uv, то загальним розв’язком рівняння є
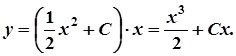
Константу інтегрування С знаходимо з початкової умови:
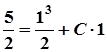 .
.
Отже, 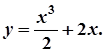
Приклад 3. Розв’яжіть задачу: знайти криву, яка проходить через точку М(0;1), якщо кутовий коефіцієнт дотичної в будь-якій точці кривої 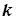 дорівнює
дорівнює 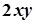 .
.
Розв’язання.
Як відомо, 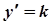 . Тому потрібно розв’язати задачу Коші:
. Тому потрібно розв’язати задачу Коші:
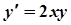 ,
, 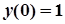 .
.
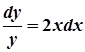 ,
, 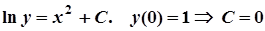 .
.
Отже, шукана крива 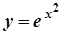 .
.
Рівняння вигляду 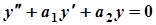 називаються лінійними однорідними Д.Р. Його загальний розв’язок має вигляд
називаються лінійними однорідними Д.Р. Його загальний розв’язок має вигляд 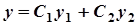 , де
, де 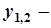 лінійно незалежні частинні розв’язки рівняння. Розшукуємо їх у вигляді
лінійно незалежні частинні розв’язки рівняння. Розшукуємо їх у вигляді 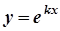 , де
, де 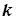 - корені характеристичного рівняння
- корені характеристичного рівняння 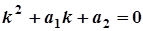 .
.
Розв’язок:
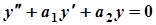
а) D>0 б) D=0, 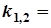 = –b/2
= –b/2
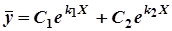 ;
; 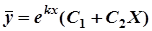 ;
;
в) D<0, 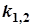 – комплексні числа.
– комплексні числа. 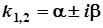
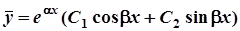 .
.
Рівняння вигляду 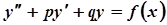 називається лінійним неоднорідним ДР 2-го порядку зі сталими коефіцієнтами.
називається лінійним неоднорідним ДР 2-го порядку зі сталими коефіцієнтами.
Для того, щоб знайти загальний розв’язок неоднорідного ДР, необхідно скористатися таким твердженням: загальний розв’язок такого ДР дорівнює сумі розв’язку відповідного однорідного ДР та якого-небудь частинного розв’язку неоднорідного ДР: 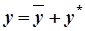 , де
, де 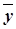 – загальний розв’язок відповідного однорідного ДР,
– загальний розв’язок відповідного однорідного ДР, 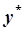 – частинний розв’язок неоднорідного ДР. Правила побудови
– частинний розв’язок неоднорідного ДР. Правила побудови 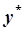 наведені у таблиці.
наведені у таблиці.
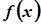 | 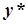 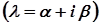 | |
| степенева частина відсутня | 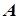 | 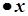 при при 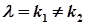 або або 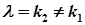 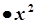 при при 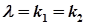 |
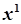 | 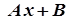 | |
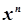 | 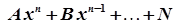 | |
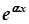 | 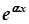 | |
показникова функція відсутня ( 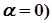 | показникова функція відсутня | |
лише 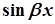 лише лише 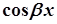 і і 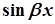 , і , і 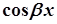 | і 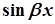 , і , і 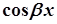 | |
тригонометричні функції відсутні ( 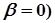 | тригонометричні функції відсутні |
Приклад 1.Розв’язати задачу Коші: 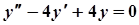 ,
, 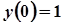 ,
, 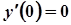 .
.
Розв’язання. Дане рівняння є лінійним однорідним ДР 2-го порядку зі сталими коефіцієнтами. Складемо характеристичне рівняння
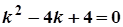 .
.
Дискримінант 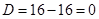 . Отже, рівняння має один дійсний корінь
. Отже, рівняння має один дійсний корінь 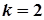 подвійної кратності. Тому загальний розв’язок ДР має вигляд
подвійної кратності. Тому загальний розв’язок ДР має вигляд
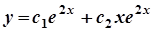 .
.
Для знаходження частинного розв’язку скористаємося початковими умовами. Для цього знайдемо 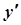 :
:
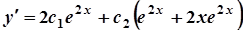 .
.
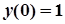
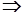
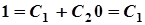 . Отже,
. Отже, 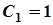 .
.
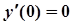
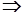
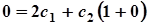 .
.
Отже, 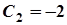 . Остаточно отримаємо
. Остаточно отримаємо 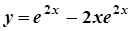 .
.
Приклад 2. Знайти загальний розв’язок лінійного неоднорідного диференціального рівняння зі сталими коефіцієнтами
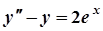 .
.
Розв'язання. 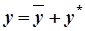 . Відповідне лінійне однорідне
. Відповідне лінійне однорідне 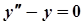 , характеристичне рівняння
, характеристичне рівняння 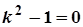 ,
, 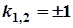 . Тоді загальний розв’язок лінійного однорідного ДР буде
. Тоді загальний розв’язок лінійного однорідного ДР буде 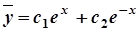 .
.
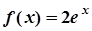 ,
, 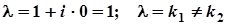 . Так як
. Так як 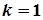 – корінь кратності
– корінь кратності 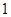 , то
, то 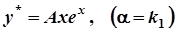 ,
,
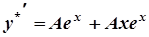 ,
, 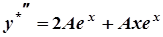 .
. 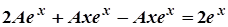 . Звідси
. Звідси 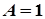 .
.
Тоді 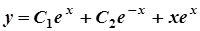 – загальний розв’язок шуканого рівняння.
– загальний розв’язок шуканого рівняння.
Приклад 3. Вказати вигляд (без обчислень коефіцієнтів)частинний розв’язок ЛНДР 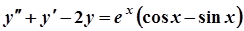 . .
. .
Розв'язання. 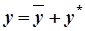 .
. 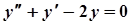 ,
, 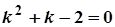 ,
, 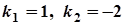 ,
, 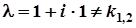
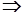
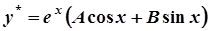 .
.
ЧИСЛОВІ РЯДИ
Нехай 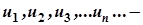 нескінченна послідовність чисел. Вираз
нескінченна послідовність чисел. Вираз 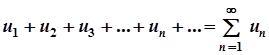 називається числовим рядом.
називається числовим рядом.
Ряд називається збіжним, якщо послідовність його часткових сум 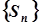 , де
, де 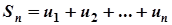 , має кінцеву границю, тобто
, має кінцеву границю, тобто 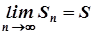 . Число
. Число 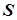 називається сумою ряду.
називається сумою ряду.
