Вероятнейшее число появлений события при повторных испытаниях
Определение 12.3.Число появлений события А в n независимых повторных испытаниях, имеющих самую наибольшую вероятность, называется наивероятнейшим числом и обозначается k0.
Пусть k0 – число появлений события А, имеющее наибольшую вероятность при n испытаниях. Тогда Рn(k0) 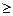 Рn(k0+1) и Рn(k0)
Рn(k0+1) и Рn(k0) 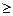 Рn(k0-1). Значит
Рn(k0-1). Значит
И .
Подставляя в эти соотношения вместо Рn(k0+1); Рn(k0); Рn(k0-1) значения, найденные по формуле Бернулли, а затем, проведя алгебраические преобразования, получим:
1)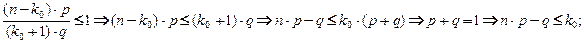
2)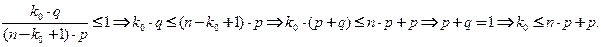
Отсюда следует, что
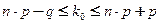 . (12.1)
. (12.1)
Числа (n·p-q) и (n·p+p) отличаются на единицу, т.к. n·p-q=n·p-1+p=n·p+p-1. Поэтому, если (n·p-q) – дробное число, то и (n·p+p) – тоже дробное, тогда неравенство (12.1) определяет одно целое число k0. Если число (n·p-q) – целое, то и (n·p+p) – тоже целое, тогда числа k0 и k0+1 будут иметь равную и наибольшую вероятность. Используя предыдущую задачу, найдем наиболее вероятное число взошедших семян.
5·0,8-0,2 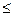 k0
k0 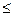 5·0,8+0,8.
5·0,8+0,8.
3,8 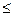 k0
k0 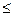 4,8.
4,8.
k0=4 Р5(4)=0,4096.
Значит, наибольшее число семян, которые произрастут, равно 4, что было видно по вычислениям.
Локальная теорема Лапласа
Пример 12.3.Медиками установлено, что 94% лиц, которым сделаны прививки против туберкулеза, приобретают иммунитет к этому заболеванию. Какова вероятность того, что среди 100000 граждан, получивших прививки, 5800 не защищены от заболевания туберкулезом?
По формуле Бернулли при n=100000; k=5800; p=0,06; q=0,94 находим
P100000(5800)=C 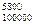 (0,06)5800(0,94)94200.
(0,06)5800(0,94)94200.
Получение ответа по формуле Бернулли при достаточно больших значениях n неудобно из-за громоздких вычислений. В этом случае применяют приближенную формулу Лапласа, которую для частного случая p= 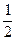 приближенно доказал Муавр в 1730 г., а затем обобщил Лаплас для p
приближенно доказал Муавр в 1730 г., а затем обобщил Лаплас для p 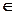 (0;1).
(0;1).
Лаплас Пьер Симон (1749–1827), выдающийся французский астроном, математик, физик, член Парижской академии наук.
Теорема 12.2 (Лаплас). Если вероятность наступления события А в каждом из n независимых испытаний постоянна и равна p, а непоявления события А равна q=1-p, то вероятность того, что событие А в серии из n испытаний появится ровно k раз, приближенно вычисляется по формуле
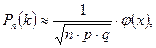 ,
,
где 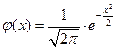 ,
, 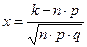 ;
;
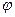 (x) – это функция Лапласа, которая затабулирована.
(x) – это функция Лапласа, которая затабулирована.
Функция Лапласа, ее свойства и график.1) Область определения: 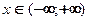 .
.
2) Функция четная и график ее симметричен относительно оси Oy.
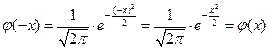 , то есть
, то есть 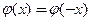
3) Исследуем функцию на экстремум.
Находим 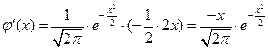 .
.
Определяем критические точки, т.е. возможные точки экстремума, для чего решаем уравнение 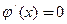
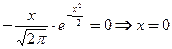 .
.
Исследуем знак производной на интервале: (- 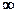 ;0) и (0;+
;0) и (0;+ 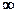 ).
).
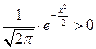 при x
при x 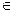 (-
(- 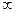 ;+
;+ 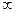 ).
).
При x 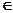 (-
(- 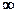 ;0)
;0) 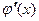 >0Þ
>0Þ 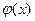 на этом интервале монотонно возрастает, при x
на этом интервале монотонно возрастает, при x 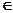 (0;+
(0;+ 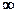 )
) 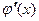 <0Þ
<0Þ 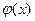 на этом интервале монотонно убывает.
на этом интервале монотонно убывает.
Значит,
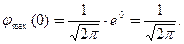
При x 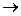
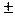
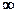
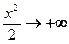 и
и 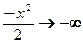 Þ
Þ
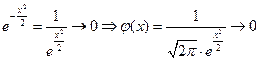 .
.
Значит, ось Ox является горизонтальной асимптотой графика функции 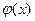 , т.е. кривая приближается к оси Ox, но никогда ее не пересекает.
, т.е. кривая приближается к оси Ox, но никогда ее не пересекает.
График этой функции имеет вид
|
| |
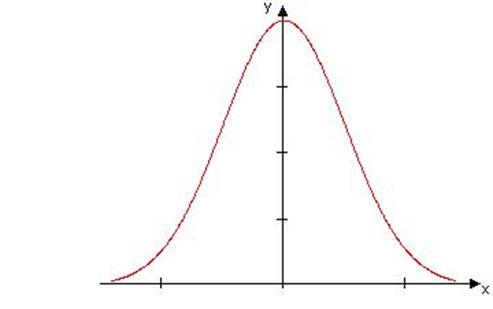
Рис. 12.1
Функцию Лапласа 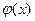 иначе называют функцией вероятностей. Значения функции
иначе называют функцией вероятностей. Значения функции 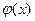 при
при 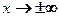 считают равными нулю.
считают равными нулю.
А теперь решим задачу из примера 12.1, т.е. вычислим
Р100000(5800) 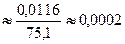 .
.
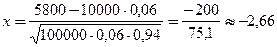 ;
;
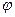 (-2,66)=
(-2,66)= 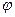 (2,66)=0,0116.
(2,66)=0,0116.
Ответ: вероятность того, что из 100000 тыс. чел. 5800 чел. не приобретут иммунитет равна 0,00002 – это практически невозможное событие.
Замечание. Расчеты, выполненные по этой формуле, дают тем точнее результат, чем больше значение n 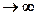 . На точность результата оказывает влияние и значение произведения p·q, т.е. произведение вероятностей появления и непоявления события в каждом испытании. Погрешность результата тем больше, чем больше будет значение p·q отличаться от 0,25; а при значениях p или q, близких к нулю, эта формула дает значительные отклонения от точных значений Рn(k), получаемых по формуле Бернулли.
. На точность результата оказывает влияние и значение произведения p·q, т.е. произведение вероятностей появления и непоявления события в каждом испытании. Погрешность результата тем больше, чем больше будет значение p·q отличаться от 0,25; а при значениях p или q, близких к нулю, эта формула дает значительные отклонения от точных значений Рn(k), получаемых по формуле Бернулли.
Пример 12.4. Вероятность вступления в законную силу вердикта народного суда по гражданскому делу равна 0,9. В течение месяца судья принял решение по 50 гражданским искам. Какова вероятность того, что 30 из них вступят в законную силу без кассационного рассмотрения? Найти наивероятнейшее число вердиктов, вступивших в силу?
Воспользуемся локальной теоремой Лапласа.
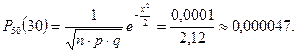
Находим 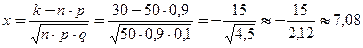 .
.
По таблице берем значение функции Лапласа: 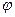 (-7,08)=
(-7,08)= 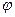 (7,08)=0,0001, т.к. для всех значений x
(7,08)=0,0001, т.к. для всех значений x 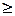 4
4 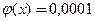 , т.е. вероятность очень мала.
, т.е. вероятность очень мала.
Находим k0:
50·0,9-0,1 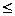 k0
k0 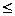 50·0,9+0,9;
50·0,9+0,9;
45-0,1 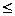 k0
k0 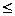 45+0,9;
45+0,9;
44,9 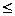 k0
k0 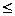 45,9.
45,9.
k0=45 – наибольшее число вердиктов, вступивших в силу.
Найдем Р50(45) 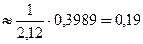 , т.к.
, т.к. 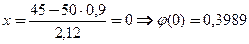 .
.
Если найдем 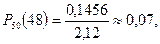 т.к.
т.к.
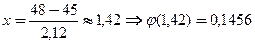 .
.
Видно, что Р50(45)>Р50(48).
Значит, наибольшее число решений, вступивших в силу, будет 45, а наибольшая вероятность Р50(45) 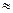 0,19. Вероятности для k>45 и k<45 очень малы.
0,19. Вероятности для k>45 и k<45 очень малы.
Пример 12.5. При въезде в новую квартиру в осветительную сеть было включено 9 лампочек. Каждая лампочка в течение года перегорает с вероятностью 0,2. Найти вероятность того, что в течение года в квартире придется заменить 5 лампочек? Наиболее вероятное число лампочек, которые придется заменить в течение года?
1) n=9; p=0,2; q=0,8; k=5 – применим формулу Бернулли.
2) Р9(5)=С 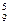 ·(0,2)5·(0,8)4=
·(0,2)5·(0,8)4= 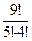 ·0,00032·0,4096=126·0,000131
·0,00032·0,4096=126·0,000131 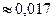 .
.
Итак, вероятность того, что в течение года придется заменить 5 лампочек равна 1,7%.
3) 9·029-0,8 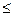 k0
k0 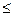 9·0,2+0,2 Þ 1
9·0,2+0,2 Þ 1 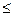 k0
k0 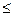 2.
2.
Так как числа целые, то k0=1 и k0+1=2 имеют равную наибольшую вероятность быть замененными в течение года.
Проверим:
Р9(1)=С 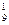 ·(0,2)1·(0,8)8=9·0,2·0,1678
·(0,2)1·(0,8)8=9·0,2·0,1678 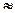 0,302.
0,302.
Р9(2)=С  ·(0,2)2·(0,8)7=36·0,04·0,2097
·(0,2)2·(0,8)7=36·0,04·0,2097  0,302.
0,302.
Пример 12.6. Вероятность встретить на улице своего учителя – 0,002. Какова вероятность того, что среди 1200 случайных прохожих вы встретите не более трех своих учителей?
Событие А – встретите среди 1200 человек не более трех своих учителей.
Событие А0 – не встретите ни одного учителя.
Событие А1 – встретите одного учителя.
Событие А2 – встретите двух учителей.
Событие А3 – встретите трех учителей.
А=А0UА1UА2UА3, причем А0; А1; А2; А3 – несовместные испытания.
Р(А)=Р(А0)+ Р(А1)+Р(А2)+Р(А3).
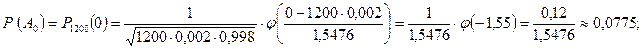
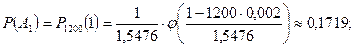
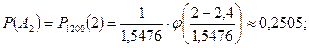
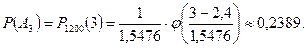
Р(А)=0,075+0,1719+0,2505+0,2389=0,7388.
Значит, гарантия того, что вы встретите не более трех своих учителей, составляет приблизительно 74%.