Определения и понятия теории дифференциальных уравнений

Эта статья является отправной точкой в изучении теории дифференциальных уравнений. Здесь собраны основные определения и понятия, которые будут постоянно фигурировать в тексте. Для лучшего усвоения и понимания определения снабжены примерами.

Дифференциальное уравнение (ДУ) – это уравнение, в которое входит неизвестная функция под знаком производной или дифференциала.

Если неизвестная функция является функцией одной переменной, то дифференциальное уравнение называют обыкновенным (сокращенно ОДУ – обыкновенное дифференциальное уравнение). Если же неизвестная функция есть функция многих переменных, то дифференциальное уравнение называют уравнением в частных производных.

Максимальный порядок производной неизвестной функции, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.

Вот примеры ОДУ первого, второго и пятого порядков соответственно

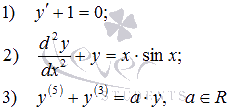
В качестве примеров уравнений в частных производных второго порядка приведем

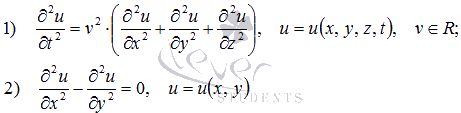
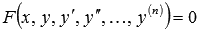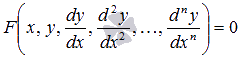Далее мы будем рассматривать только обыкновенные дифференциальные уравнения n-ого порядка вида или , где Ф(x, y) = 0 неизвестная функция, заданная неявно (когда возможно, будем ее записывать в явном представлении y = f(x)).

Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения.

Решение дифференциального уравнения - это неявно заданная функция Ф(x, y) = 0 (в некоторых случаях функцию y можно выразить через аргумент x явно), которая обращает дифференциальное уравнение в тождество.

ОБРАТИТЕ ВНИМАНИЕ.

Решение дифференциального уравнения всегда ищется на заранее заданном интервале X.

Почему мы об этом говорим отдельно? Да потому что в условиях многих задач об интервале X не упоминают. То есть, обычно условие задач формулируется так: «найдите решение обыкновенного дифференциального уравнения 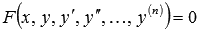». В этом случае подразумевается, что решение следует искать для всех x, при которых и искомая функция y, и исходное уравнение имеют смысл.

Решение дифференциального уравнения часто называют интегралом дифференциального уравнения.

Функци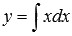и или 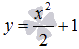можно назвать решением дифференциального уравнения .

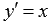Одним из решений дифференциального уравнения 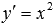является функция 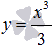. Действительно, подставив эту функцию в исходное уравнение, получим тождество 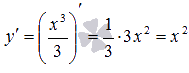. Несложно заметить, что другим решением этого ОДУ является, например, 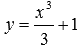. Таким образом, дифференциальные уравнения могут иметь множество решений.

Общее решение дифференциального уравнения – это множество решений, содержащее все без исключения решения этого дифференциального уравнения.

Общее решение дифференциального уравнения еще называют общим интегралом дифференциального уравнения.

Вернемся к примеру. Общее решение дифференциального уравнения 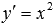имеет вид 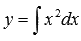или 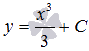, где C – произвольная постоянная. Выше мы указали два решения этого ОДУ, которые получаются из общего интеграла дифференциального уравнения 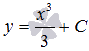при подстановке С = 0 и C = 1 соответственно.

Если решение дифференциального уравнения удовлетворяет изначально заданным дополнительным условиям, то его называют частным решением дифференциального уравнения.

Частным решением дифференциального уравнения 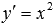, удовлетворяющим условию y(1)=1, является 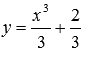. Действительно, 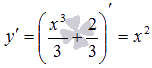и .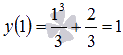

Основными задачами теории дифференциальных уравнений являются задачи Коши, краевые задачи и задачи нахождения общего решения дифференциального уравнения на каком-либо заданном интервале X.

Задача Коши – это задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям 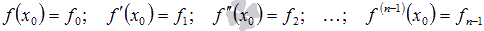, где 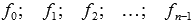- числа.

Краевая задача – это задача нахождения частного решения дифференциального уравнения второго порядка, удовлетворяющего дополнительным условиям в граничных точках x₀ и x₁ :
f (x₀) = f₀ , f (x₁) = f₁ , где f₀ и f₁ - заданные числа.

Краевую задачу часто называют граничной задачей.

Обыкновенное дифференциальное уравнение n-ого порядка называется линейным, если оно имеет вид 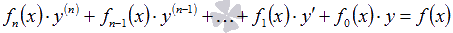, а коэффициенты 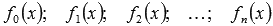есть непрерывные функции аргумента x на интервале интегрирования.

Если 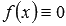, то уравнение 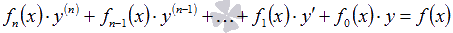называют линейным однородным дифференциальным уравнением (ЛОДУ), в противном случае – линейным неоднородным дифференциальным уравнением (ЛНДУ).

Когда коэффициенты 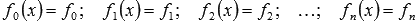являются постоянными функциями (то есть, некоторыми числами), то соответствующие дифференциальные уравнения называют ЛОДУ с постоянными коэффициентами (если 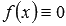) или ЛНДУ с постоянными коэффициентами (при ненулевой f(x)).

Характеристическое уравнение линейного однородного дифференциального уравнения n-ой степени с постоянными коэффициентами – это уравнение n-ой степени вида .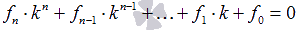

Теперь Вы знакомы с основными определениями и понятиями. Дополнительные определения будем давать по мере изложения теории. Далее рекомендуем изучить основные виды дифференциальных уравнений и методы решения.

2.2)