Если последовательность имеет предел, то этот предел единственный
Математика для экономистов
Курс лекций
для студентов дневной и заочной формы обучения
Авторы:
Шепеленко О.В., Щетинина Е.К., Скрыпник С.В.,
Фомина Т.А., Саркисьянц Е.В.
Затверджено:
Протокол засідання кафедри
вищої і прикладної математики
№ 25 від 15.04.2010 р.
Донецьк 2010
С о д е р ж а н и е
| стр. | |
| 1. Элементы теории пределов……………………………………………………... | |
| 1.1. Предел последовательности………………………………………………..... | |
| 1.2. Предел функции…………………………………………………………….… | |
| 1.3. Раскрытие неопределенностей ……………………………………………... | |
| 1.4. Первый замечательный предел……………………………………………… | |
| 1.5. Второй замечательный предел ……………………………………………… | |
| 2. Производная функции…………………………………………………………… | |
| 2.1. Понятие производной функции…………………………………………..... | |
| 2.2. Производная сложной функции…………………………………………..... | |
| 2.3. Дифференцирование неявной функции……………………………….… | |
| 3. Применение производной к исследованию функции………………….… | |
| 3.1. Экстремум функции………………………………………………………….. | |
| 3.2. Точки перегиба………………………………………………………………… | |
| 3.3. Асимптоты ……………………………………………………………………… | |
| 3.4. Общая схема исследования функции и построение ее графика……… | |
| 4. Неопределенный интеграл……………………………………………………… | |
| 4.1. Первообразная функция и неопределенный интеграл………………… | |
| 4.2. Непосредственное интегрирование ……………………………………….. | |
| 4.3. Интегрирование методом замены переменной (метод подстановки)….. | |
| 4.4. Интегрирование по частям ………………………………………………….. | |
| 4.5. Интегрирование рациональных дробей………………………………….. | |
| 4.6. Интегрирование тригонометрических функций ………………………. | |
| 5. Определенный интеграл ………………………………………………………... | |
| 5.1. Понятие определенного интеграла………………………………………… | |
| 5.2. Формула Ньютона-Лейбница……………………………………………….. | |
| 5.3. Методы интегрирования……………………………………………………... | |
| 6. Несобственный интеграл ………………………………………………………... | |
| 7. Дифференциальные уравнения……………………………………………….. | |
| 7.1. Уравнения с разделяющимися переменными……………………………. | |
| 7.2. Однородные дифференциальные уравнения первого порядка ……… | |
| 7.3. Линейные дифференциальные уравнения первого порядка…………. | |
| 7.4. Дифференциальные уравнения второго порядка………………………. | |
| 7.5. Дифференциальные уравнения второго порядка с постоянными коэффициентами………………………………………….. | |
| 8. Числовые ряды ……………………………………………………………………. | |
| 8.1. Необходимый признак сходимости числового ряда…………………….. | |
| 8.2. Достаточные признаки сходимости знакоположительных рядов…….. | |
| 8.3. Знакочередующиеся ряды…………………………………………………… | |
| 9. Степенные ряды…………………………………………………………………… | |
| Литература ……………………………………………………………………………. |
| 1. Элементы теории пределов |
1.1. Предел последовательности
| Определение. | Числовой последовательностью называется функция 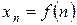 натурального аргумента. натурального аргумента. |
Член 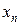 называется общим членом последовательности. Последовательность с общим членом
называется общим членом последовательности. Последовательность с общим членом 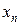 содержит бесконечное множество чисел и обозначается
содержит бесконечное множество чисел и обозначается 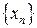 . Последовательность считается заданной, если дан способ вычисления любого ее члена по его известному номеру.
. Последовательность считается заданной, если дан способ вычисления любого ее члена по его известному номеру.
Пример.Написать первые 10 членов последовательности, если ее общий член 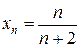 .
.
Решение. Вычисляя значение дроби 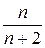 при значениях
при значениях 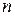 , равных 1, 2, 3,…, 10, получим:
, равных 1, 2, 3,…, 10, получим: 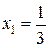 ,
, 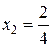 ,
, 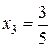 ,
, 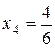 ,
, 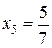 ,
, 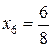 ,
, 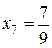 ,
, 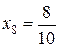 ,
, 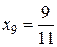 ,
, 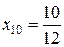 .
.
В общем виде: 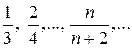
| Определение. | Число 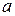 называется пределомпоследовательности называется пределомпоследовательности 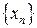 , если для любого, даже сколь угодно малого, положительного числа , если для любого, даже сколь угодно малого, положительного числа 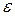 найдется такое натуральное число найдется такое натуральное число 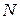 , , |
что все значения переменной 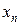 , начиная с
, начиная с 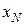 , отличаются от
, отличаются от 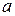 по абсолютной величине меньше чем на
по абсолютной величине меньше чем на 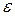 :
:
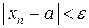
при всех 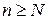 , или
, или
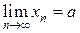 .
.
Если последовательность имеет предел, то этот предел единственный.
Если последовательность 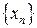 имеет предел, равный
имеет предел, равный 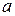 , то говорят, что эта последовательность сходится к
, то говорят, что эта последовательность сходится к 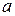 . Например, поскольку
. Например, поскольку 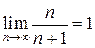 , то говорят, что последовательность
, то говорят, что последовательность 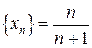 сходится к 1.
сходится к 1.
Последовательность, не имеющая предела, называется расходящейся. Например, последовательность 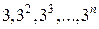 ,… не имеет предела, значит она расходится.
,… не имеет предела, значит она расходится.
Геометрическая интерпретация предела. Постоянное число 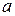 называется пределомпеременной
называется пределомпеременной 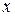 , если для любой окрестности с центром в точке
, если для любой окрестности с центром в точке 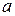 , даже сколь угодно малого радиуса
, даже сколь угодно малого радиуса 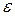 , найдется такое значение
, найдется такое значение 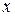 , что точки, изображающие это значение и все последующие значения переменной
, что точки, изображающие это значение и все последующие значения переменной 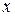 , попадут в эту окрестность (рис.1). Обратим внимание на то, что вне любой окрестности точки
, попадут в эту окрестность (рис.1). Обратим внимание на то, что вне любой окрестности точки 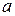 лежит лишь конечное число значений переменной
лежит лишь конечное число значений переменной 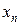 .
.
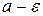
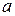
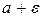
 |
0 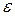
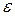
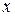
Рис. 1 Геометрическая интерпретация предела последовательности
Предел функции
| Определение. | Число 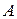 является пределом функции является пределом функции 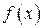 при при 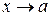 , если для любого, даже сколь угодно малого, положительного числа , если для любого, даже сколь угодно малого, положительного числа 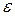 существует такое положительное число существует такое положительное число 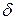 , что для всех , что для всех 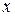 , удовлетворяющих условию , удовлетворяющих условию 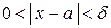 , выполняется неравенство , выполняется неравенство 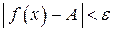 . . |
Тот факт, что функция 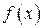 при
при 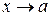 имеет предел, равный
имеет предел, равный 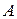 , символически обозначают в виде
, символически обозначают в виде
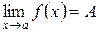 .
.
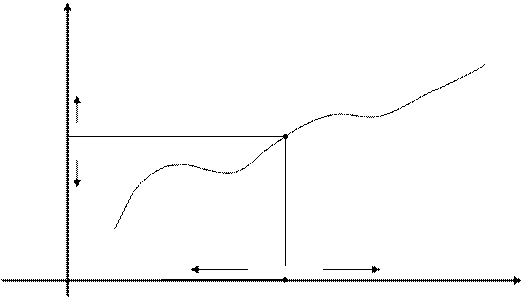
Геометрическая интерпретация. Пусть дан график функции 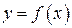 , имеющей предел при
, имеющей предел при 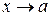 , равный
, равный 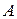 (рис.2).
(рис.2).
Для каждого наперед заданного значения 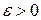 , найдется окрестность точки
, найдется окрестность точки 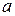 радиуса
радиуса 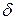 , такая, что часть графика данной функции, соответствующая окрестности
, такая, что часть графика данной функции, соответствующая окрестности 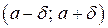 , содержится внутри полосы, ограниченной прямыми
, содержится внутри полосы, ограниченной прямыми 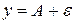 ,
, 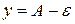 .
.
 |  | |||||||||||||||||||||||||
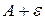 | ||||||||||||||||||||||||||
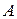 | 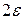 | 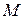 | ||||||||||||||||||||||||
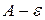 | ||||||||||||||||||||||||||
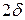 | ||||||||||||||||||||||||||
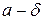 | 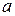 | 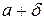 | 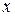 |
Рис. 2 Геометрическая интерпретация предела функции
