РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №6

Тема: «Геометрические характеристики плоских сечений»

Цель работы:

Определение моментов инерции сложных фигур, составленных из простых геометрических фигур и стандартных прокатных профилей

Студент должен знать:

1. моменты инерции простых сечений;
2. методику определения главных осей инерции;

Студент должен уметь:

1. определять моменты инерции сечения с одной или двумя осями симметрии;
2. определять моменты инерции сечения, составленного из стандартных прокатных профилей.

Вопросы для самоконтроля:

1. Как определяются координаты центра тяжести фигуры?
2. Какие моменты инерции называются осевыми, полярными и центробежными?
3. Каковы единицы измерения моментов инерции?
4. Напишите формулу перехода для осевого момента инерции при параллельном переносе осей.
5. Напишите формулу осевых моментов инерции для простых геометрических фигур.
6. Как определить момент инерции составного сечения?
7. Как определить моменты инерции стандартных прокатных профилей?
8. Что называется главными осями инерции?
9. Что называется главными моментами инерции?

Методические указания

1. Определить положение центра тяжести сечения (см. порядок решения задачи для расчетно-графической работы № 3).

2. Провести центральные оси для каждого профиля проката или простой геометрической фигуры. Эти оси называются центральными осями. Для первой фигуры проводят оси х₁ и у₁, для второй — х₂ и у₂ и т.д.

3. Провести главные центральные оси. Они проходят через центр тяжести всего сечения. Одну из осей совмещают с осью симметрии (в задании все сечения имеют такую ось), а вторую проводят через центр тяжести сечения перпендикулярно первой. Вертикальная ось обозначается 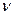, а горизонтальная — u.

4. Найти моменты инерции сечения относительно главных центральных осей. В общем виде моменты инерции сечения определяют по формулам:

относительно оси u

относительно оси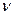

где J_u и J 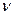— моменты инерции сечения относительно главных центральных осей u и 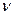(главные центральные моменты инерции); J , J , …, J — моменты инерции простых фигур (1, 2,..., n) относительно главной центральной оси u; J , J , …, J — то же, относительно оси .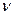

Моменты инерции простых фигур относительно осей u и 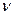определяются по формулам:

относительно оси u

относительно оси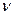

где 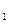J_х , J_{х , …,} J_х — моменты инерции простых фигур (1, 2, …, n) относительно собственных центральных осей х₁, х ₂,..., х_n. Они определяются по таблицам ГОСТов (см. прил. 1) для профилей прокатной стали и формулам для простых геометрических фигур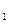; J_у , J_у , …, Jу — то же, относительно осей у₁, у₂, ..., у_n; а₁, а₂, ..., а_n — расстояние от главной центральной оси u до центральных осей х₁, х₂, ..., х_n; b₁, b₂, …, b_n. — то же, от оси 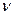до осей у₁, у₂, ..., у_n; А₁, А₂, ..., А_n — площади сечений профилей прокатной стали или простых геометрических фигур.

Если главная центральная ось совпадает с собственной центральной осью какого-нибудь профиля или фигуры, то момент инерции ее относительно главной центральной оси равен моменту инерции относительно собственной оси, так как расстояние между ними равно нулю.

При определении геометрических характеристик необходимо учитывать, что профили проката на заданном сечении могут быть ориентированы иначе, чем в ГОСТах. Например, вертикальная по ГОСТу ось у на заданном сечении может оказаться горизонтальной, а горизонтальная ось х — вертикальной. Поэтому необходимо внимательно следить за тем, относительно каких осей следует брать геометрические характеристики.

Пример 1. Определить главные моменты инерции сечения, показанного на рис. 19. Сечение состоит из двух уголков 56 4 и швеллера № 18.

рис. 19

Решение

1. Определить положение центра тяжести сечения (см. расчетно-графическую работу № 3). Координаты центра тяжести: х_с = О; у_с = 2,43 см.

2. Провести центральные оси х₁, х₂, х₃ и оси у₁, у₂, у₃ через центры тяжести фигур 1, 2, 3.

3. Провести главные центральные оси. Ось 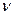совместим с осью симметрии у₃. Ось u проведем через центр тяжести сечения С перпендикулярно 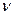оси . Оси 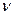и у₃ совпали.

4. Определить главный момент инерции относительно оси u:

Из рис.19 следует, что уголки одинаковые и расположены на одинаковом расстоянии от оси u, т. е. А₁ = А₂ и а₁ = а₂.

Поэтому формулу для определения можно записать:

Пример 2. Определить момент инерции сечения, показанного на рис. 20, относительно главной центральной оси, не являющейся осью симметрии сечения. Сечение состоит из двутавра №24 и швеллера № 24а.

рис. 20

Решение

1. Центр тяжести сечения найден в расчетно-графической работе № 3 (х_с = 6,11 см;

у_с = 0).

2. Провести центральные оси х₁, х₂ и у₁, у₂. Оси х₁ и х₂ совпали.

3. Провести главные центральные оси. Ось u совмещаем с осью симметрии, а ось 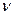проводим через центр тяжести С перпендикулярно оси u. Оси u, х₁ и х₂ совпали.

4. Определить момент инерции сечения относительно оси 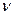, так как по условию требуется найти момент инерции только относительно оси, не являющейся осью симметрии. Записать формулу

В этой формуле

Задание для расчетно-графической работы 6 (пример 1). Определить главные моменты инерции сечения, составленного из стандартных прокатных профилей (исходные данные взять из расчетно-графической работы № 3 по теоретической механике).

Задание для расчетно-графической работы 6 (пример 2). Определить главные моменты инерции сечения, составленного из простых геометрических фигур (исходные данные взять из расчетно-графической работы № 3 по теоретической механике).