Нули функции: нет 6) Промежутки знакопостоянства: y>0 если ( ) y<0, нет таких Х
Промежутки убывания: нет 5) Нули функции: 6) Промежутки знакопостоянства: y>0 если ( ) y<0, нет таких Х
2) 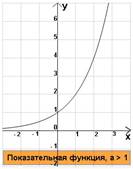 Показательная функция
Показательная функция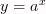 , где a > 1
, где a > 1
Свойства:
1) Область определения:
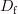 = (
= ( 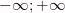 )
)
2) Область значений:
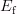 = (
= ( 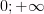 )
)
3) Промежуток возрастания:
Промежутки убывания: нет 5) Нули функции: нет 6) Промежутки знакопостоянства: y>0 если ( ) y<0, нет таких Х
3)  Показательная функция
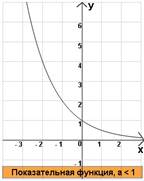
Показательная функция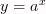 , где a < 1
, где a < 1
Свойства:
1) Область определения:
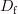 = (
= ( 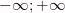 )
)
2) Область значений:
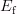 = (
= ( 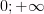 )
)
3) Промежутки возрастания: нет
4) Промежуток убывания:
Нули функции: нет 6) Промежутки знакопостоянства: y>0 если ( ) y<0, нет таких Х
4) 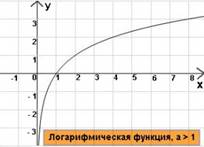 Логарифмическая функция
Логарифмическая функция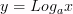 , a > 1
, a > 1
Свойства:
1) Область определения:
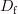 = (
= ( 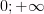 )
)
2) Область значений:
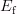 = (
= ( 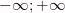 )
)
3) Промежуток возрастания: ( 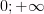 )
)
4) Промежуток убывания: нет
5) Нули функции: x=1
6) Промежутки знакопостоянства:
y>0 если 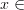 (
( 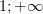 )
)
y<0 если 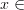 (
( 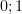 )
)
5) Логарифмическая функция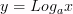 , a < 1
, a < 1
Свойства:
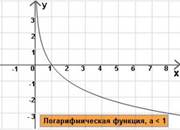 1) Область определения:
1) Область определения:
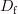 = (
= ( 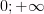 )
)
2) Область значений:
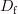 =(
=( 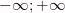 )
)
3) Промежуток возрастания: нет
4) Промежуток убывания:( 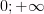 )
)
5) Нули функции: x=1
6) Промежутки знакопостоянства:
y>0 если 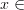 (
( 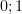 )
)
y<0 если 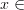 (
( 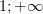 )
)
6) 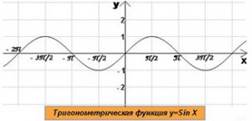 Тригонометрическая функция
Тригонометрическая функция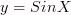
Свойства:
1) Область определения:
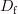 =(
=( 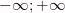 )
)
2) Область значений:
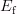 =[
=[ 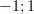 ]
]
3) Промежутки возрастания: [ 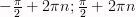 ], где
], где 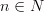
4) Промежутки убывания: [ 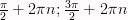 ], где
], где 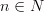
5) Нули функции: 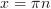 , где
, где 
6) Промежутки знакопостоянства:
y>0 если 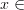 [
[ 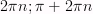 ], где
], где 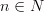
y<0 если 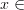 [
[ 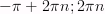 ], где
], где 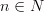
7) 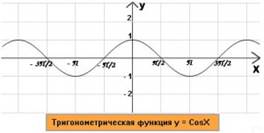 Тригонометрическая функция
Тригонометрическая функция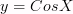
Свойства:
1) Область определения:
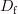 =(
=( 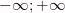 )
)
2) Область значений:
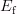 =[
=[ 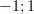 ]
]
3) Промежутки возрастания: [ 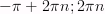 ], где
], где 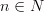
4) Промежутки убывания: [ 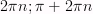 ], где
], где 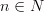
5) Нули функции: 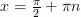 , где
, где 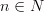
6) Промежутки знакопостоянства:
y>0 если 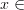 [
[ 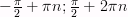 ], где
], где 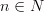
y<0 если 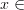 [
[ 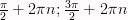 ], где
], где 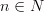
2. Предел функции
Предел функции. ЧислоL называется пределом функции y = f ( x ) при x, стремящемся к a :
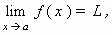
если для любого 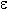 > 0 найдётся такое положительное число
> 0 найдётся такое положительное число 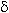 =
= 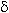 (
( 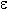 ), зависящее от
), зависящее от 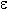 , что из условия | x a | <
, что из условия | x a | < 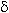 следует | f ( x ) – L | <
следует | f ( x ) – L | < 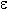
Это определение означает, что L есть предел функции y = f ( x ), если значение функции неограниченно приближается к L , когда значение аргумента x приближается к a. Геометрически это значит, что для любого 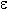 > 0 можно найти такое число
> 0 можно найти такое число 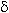 , что если x находится в интервале ( a
, что если x находится в интервале ( a 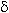 a
a 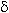 ), то значение функции лежит в интервале ( L
), то значение функции лежит в интервале ( L 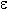 , L +
, L + 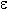 ). Отметим, что в соответствии с этим определением аргумент функции лишь приближается к a , не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.
). Отметим, что в соответствии с этим определением аргумент функции лишь приближается к a , не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.
3. Основные теоремы о пределах.
Теорема 1. (о предельном переходе в равенстве)Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
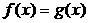 Þ
Þ 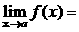
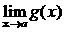 .
.
Теорема 2. (о предельном переходе в неравенстве)Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).
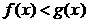 Þ
Þ 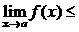
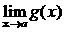 .
.
Теорема 3. Предел постоянной равен самой постоянной.
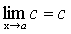 .
.
Доказательство. f(x)=с, докажем, что 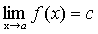 .
.
Возьмем произвольное e>0. В качестве d можно взять любое
положительное число. Тогда при 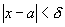
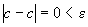 .
.
Теорема 4. Функция не может иметь двух различных пределов в
одной точке.
Доказательство. Предположим противное. Пусть
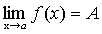 и
и 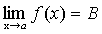 .
.
По теореме о связи предела и бесконечно малой функции:
f(x)-A= 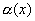 - б.м. при
- б.м. при 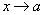 ,
,
f(x)-B= 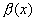 - б.м. при
- б.м. при 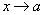 .
.
Вычитая эти равенства, получим: 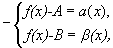
B-A= 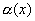 -
- 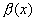 .
.
Переходя к пределам в обеих частях равенства при 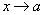 , имеем:
, имеем:
B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.
Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при 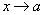 , то и алгебраическая сумма имеет предел при
, то и алгебраическая сумма имеет предел при 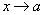 , причем предел алгебраической суммы равен алгебраической сумме пределов.
, причем предел алгебраической суммы равен алгебраической сумме пределов.
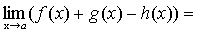
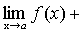
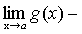
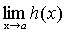 .
.
Доказательство. Пусть 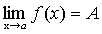 ,
, 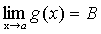 ,
, 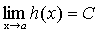 .
.
Тогда, по теореме о связи предела и б.м. функции:
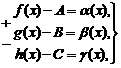 где
где 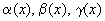 - б.м. при
- б.м. при 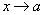 .
.
Сложим алгебраически эти равенства:
f(x)+g(x)-h(x)-(А+В-С)= 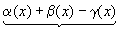 ,
,
где 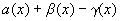 б.м. при
б.м. при 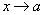 .
.
По теореме о связи предела и б.м. функции:
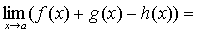 А+В-С=
А+В-С= 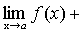
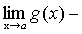
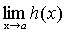 .
.
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при 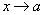 , то и произведение имеет предел при
, то и произведение имеет предел при 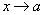 , причем предел произведения равен произведению пределов.
, причем предел произведения равен произведению пределов.
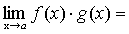
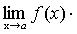
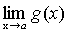 .
.
Следствие. Постоянный множитель можно выносить за знак предела.
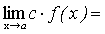
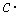
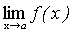 .
.
Теорема 7. Если функции f(x) и g(x) имеют предел при 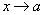 ,
,
причем 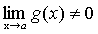 , то и их частное имеет предел при
, то и их частное имеет предел при 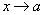 , причем предел частного равен частному пределов.
, причем предел частного равен частному пределов.
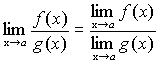 ,
, 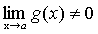 .
.
4. Непрерывность функции в точке и на интервале.
Непрерывность функции в точке.
Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точкех0, если предел функции и ее значение в этой точке равны, т.е.
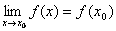
Тот же факт можно записать иначе: 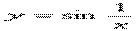
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию
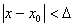
верно неравенство 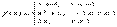 .
.
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + a(x)
где a(х) – бесконечно малая при х®х0.
Непрерывность функции на интервале и на отрезке.
Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
5. Производная и дифференциал.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.
Дифференциал функции 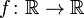 в точке
в точке 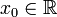 может быть определён как линейная функция
может быть определён как линейная функция
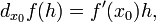
где 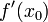 обозначает производную
обозначает производную 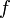 в точке
в точке 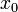 .
.
Таким образом 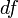 есть функция двух аргументов
есть функция двух аргументов 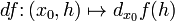 .
.
Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция 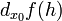 линейно зависящая от
линейно зависящая от 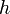 и для которой верно следующее соотношение
и для которой верно следующее соотношение
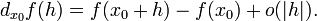
6. Основные теоремы о дифференцируемых функциях.
1. Теорема. Ролля. Если функция g(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка и на концах обращается в нуль g(a)=g(b)=0, то существует по крайней мере одна точка a < c < b в которой производная gў обращается в нуль gў(c)=0.
2 Теорема. Лагранжа. Если функция g(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка, то существует по крайней мере одна точка a < c < b в которой выполняется равенство g(b)-g(a)=gў(c)(b-a)
3. Теорема. Коши. Если функции g(x) и h(x) непрерывны на отрезке [a,b], дифференцируемы во всех внутренних точках этого отрезка, причем hў(x) № 0 внутри отрезка [a,b], то существует точка a < c < b в которой выполняется равенство
| g(b)-g(a) h(b)-h(a) | = | gў(c) hў(c) |
4. Теорема. Лопиталя. Пусть функции g(x) и h(x) на некотором отрезке [a,b] удовлетворяют условиям теоремы Kоши и обращаются в 0 в точке x=a, т.е. g(a)=h(a)=0, тогда если существует предел отношения gў(x)/hў(x) при x® a, то существует и
| lim x® a | g(x)/h(x) |
причем
| lim x® a | gў(x)/hў(x)= | lim x® a | g(x)/h(x). |
7. Функции нескольких переменных и их непрерывность.
Определение 1. Функцией n переменных u (x1, x2, … , xn) называется отображение u: Rn → R , т.е. любое правило, которое каждой точке x = (x1, x2, … , xn) О D М Rn ставит в соответствие действительное число u О R .
D М Rn называется областью определения функции u и записывается D(u) .
Функцию n переменных записывают так: u = f(x1, x2, … , xn) .
Пространство Rn считаем евклидовым с ортонормированным базисом.
Пусть функция n переменных u = f(x) = f(x1, x2, … , xn) определена в некоторой окрестности точки a = (a1, a2, … , an) О Rn (включая саму точку a).
Определение 1. Функция u = f(x) называется непрерывной в точке a, если
f(x) = f(a). |
Обозначим приращения аргументов символами Δx1 = x1 − a1, Δx2 = x2 − a2, …, Δxn = xn − an. Соответствующее приращение функции u=f(x)
| Δu = f(a1 + Δx1, a2 + Δx2, … , an + Δxn) − f(a1, a2, … , an). |
называется полным приращением функции u=f(x) в точке a, соответствующим прирашению
Δx = {Δx1, Δx2, …, Δxn}.
Условие, определяющее непрерывную функцию u = f(x) в точке a эквивалентно условию
Δu = 0. |
Приращение
| δxku = f(a1, … , ak + Δxk, … , an) − f(a1, a2, … , an) |
называется частным приращением функции u в точке a, соответствующим приращению Δxk аргумента xk.
Определение 2. Функция u = f(x) = f(x1, x2, … , xn) называется непрерывной в точке a = (a1, a2, … , an) по переменной xk , если
δxku = 0. | ||
8. Производные функции нескольких переменных.
Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:
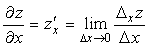
– это частная производная функции z по аргументу x;
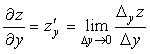
– это частная производная функции z по аргументу у.
Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.
9. Дифференциалы функций нескольких переменных.
Дифференциал функции нескольких переменныхопределяется как линейная (относительно приращений аргументов) часть приращения дифференцируемой функции
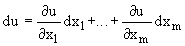 ,
,
где dxi 
 xi (i=1, ..., m), если x1, ..., xm - независимые переменные.
xi (i=1, ..., m), если x1, ..., xm - независимые переменные.
Как и в случае одной переменной первый дифференциал обладает свойством инвариантности его формы, т.е. выражение для первого дифференциала имеет тот же вид и в случае, когда х1, ..., хm являются функциями некоторых переменных t1, ..., tk. Свойство инвариантности формы первого дифференциала позволяет установить следующие формулы
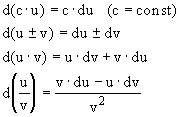
10. Поиск экстремума функции нескольких переменных.
Функция 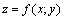 имеет максимум (минимум) в точке
имеет максимум (минимум) в точке 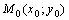 , если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке
, если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке 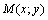 некоторой окрестности точки
некоторой окрестности точки 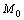 , то есть
, то есть 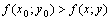 (соответственно
(соответственно 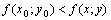 ) для всех точек
) для всех точек 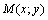 , принадлежащих этой окрестности. Максимум и минимум функции называется ее экстремумом. Точка
, принадлежащих этой окрестности. Максимум и минимум функции называется ее экстремумом. Точка 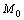 , в которой функция имеет экстремум, называется точкой экстремума.
, в которой функция имеет экстремум, называется точкой экстремума.
Необходимое условие экстремума: если дифференцируемая функция 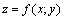 достигает экстремума в точке
достигает экстремума в точке 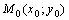 , то ее частные производные первого порядка в этой точке равны нулю, то есть:
, то ее частные производные первого порядка в этой точке равны нулю, то есть: 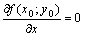 ,
, 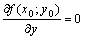 .
.
Точки, в которых частные производные равны нулю, называются стационарными точками. Стационарные точки и точки, в которых производные не существуют и которые лежат внутри области определения функции, называются критическими точками. Не всякая критическая точка является точкой экстремума.
Достаточное условие существования экстремума:
Пусть 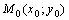 стационарная точка функции
стационарная точка функции 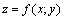 . Обозначим
. Обозначим 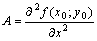 ,
, 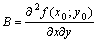 ,
, 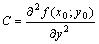 и составим дискриминант
и составим дискриминант 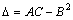 . Тогда:
. Тогда:
если 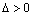 , то функция имеет в точке
, то функция имеет в точке 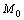 экстремум, а именно максимум, при
экстремум, а именно максимум, при 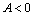 (или
(или 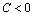 ) и минимум, при
) и минимум, при 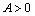 (или
(или 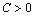 );
);
если 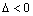 , то в точке
, то в точке 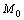 экстремума нет;
экстремума нет;
если 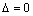 , то требуется дальнейшее исследование (сомнительный случай).
, то требуется дальнейшее исследование (сомнительный случай).
11. Поиск экстремума функции двух переменных.
Пусть функция 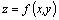 определена в некоторой области G и точка
определена в некоторой области G и точка 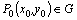 .
.
Функция 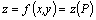 имеет в точке
имеет в точке 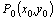 максимум, если существует такая окрестность этой точки, что для всех точек
максимум, если существует такая окрестность этой точки, что для всех точек 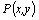 этой окрестности, отличных от
этой окрестности, отличных от 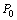 , выполняется неравенство
, выполняется неравенство 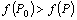 .
.
Аналогично определяется минимум функции.
Максимум и минимум функции называются экстремумами функции.
Теорема (необходимое условие экстремума). Если 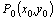 –точка экстремума функции
–точка экстремума функции 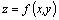 , то частные производные
, то частные производные 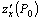 и
и 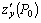 в этой точке равны нулю или не существуют.
в этой точке равны нулю или не существуют.
Точки, в которых частные производные 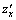 и
и 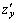 обращаются в нуль или не существуют, называются критическими точками этой функции.
обращаются в нуль или не существуют, называются критическими точками этой функции.
Сформулированный признак не является достаточным: не обязательно критическая точка является точкой экстремума.
Чтобы проверить, есть ли экстремум в критической точке, используют следующую теорему (достаточное условие экстремума).
Пусть в некоторой области, содержащей точку 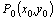 , функция
, функция 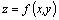 имеет непрерывные частные производные до 3–го порядка включительно и
имеет непрерывные частные производные до 3–го порядка включительно и 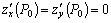 . Обозначим:
. Обозначим: 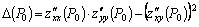 . Тогда
. Тогда
1)если 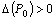 , то функция имеет экстремум в точке
, то функция имеет экстремум в точке 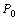 , причем это максимум, если
, причем это максимум, если 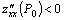 и минимум, если
и минимум, если 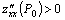 ;
;
2)если 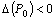 , то экстремума в точке
, то экстремума в точке 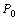 нет;
нет;
3)если 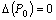 , требуется дополнительное исследование (экстремум в точке
, требуется дополнительное исследование (экстремум в точке 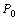 может быть или не быть).
может быть или не быть).
12. Неопределенный интеграл. Основные теоремы ( не могу найти).
Неопределённый интегра́л для функции 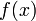 — это совокупность всех первообразных данной функции.
— это совокупность всех первообразных данной функции.
Если функция 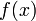 определена и непрерывна на промежутке
определена и непрерывна на промежутке 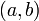 и
и 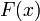 — её первообразная, то есть
— её первообразная, то есть 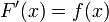 при
при 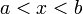 , то
, то
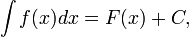
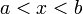 ,
,
где С — произвольная постоянная.
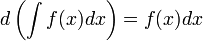
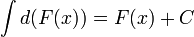
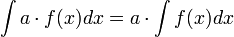
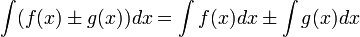
Если 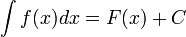 , то и
, то и 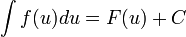 , где
, где 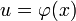 — произвольная функция, имеющая непрерывную производную
— произвольная функция, имеющая непрерывную производную
13. Интегрирование подстановкой.
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 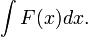 Сделаем подстановку
Сделаем подстановку 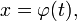 где
где 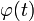 — функция, имеющая непрерывную производную.
— функция, имеющая непрерывную производную.
Тогда 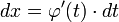 и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
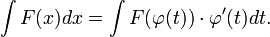
14. Интегрирование по частям.
Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы
для неопределённого интеграла:
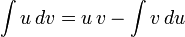
для определённого:
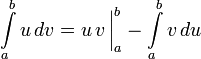
15. Интегрирование рациональной функции.
Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.
Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.
Всякую правильную рациональную дробь 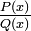 , знаменатель которой разложен на множители
, знаменатель которой разложен на множители
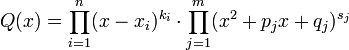
можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:
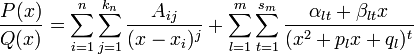
где 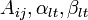 — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.
— некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.
16. Определенный интеграл, основные теоремы.
Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).
Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.
Пусть 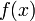 определена на
определена на 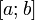 . Разобьём
. Разобьём 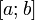 на части с несколькими произвольными точками
на части с несколькими произвольными точками 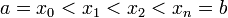 Тогда говорят, что произведено разбиение
Тогда говорят, что произведено разбиение 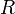 отрезка
отрезка 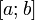 Далее выберем произв. точку
Далее выберем произв. точку 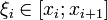 ,
, 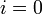 , Определённым интегралом от функции
, Определённым интегралом от функции 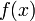 на отрезке
на отрезке 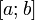 называется предел интегральных сумм
называется предел интегральных сумм 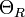 при
при 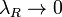 , если он существует независимо от разбиения
, если он существует независимо от разбиения 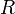 и выбора точек
и выбора точек 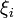 , т.е.
, т.е. 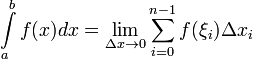 (1) Если существует (1), то функция
(1) Если существует (1), то функция 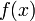 называется интегрируемой на
называется интегрируемой на 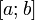 – определение интеграла по Риману.
– определение интеграла по Риману.
-
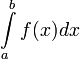
-
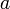 – нижний предел.
– нижний предел. -
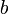 – верхний предел.
– верхний предел. -
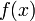 – подынтегральная функция.
– подынтегральная функция. -
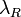 - длина частичного отрезка.
- длина частичного отрезка. -
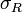 – интегральная сумма от функции
– интегральная сумма от функции 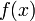 на
на 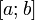 соответствующей разбиению
соответствующей разбиению 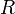 .
. -
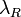 - максимальная длина част. отрезка.
- максимальная длина част. отрезка.
Определение интеграла на языке  ,
, 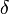 :(по "Коши") Число I – называется определённым интегралом от f(x) на [ a ; b ], если для любого ε>0 существует δ=δ(ε)>0: для любого разбиения R отрезка [ a ; b ]: λR < δ, выполняется неравенство: |I- σR | = |∑n-1i=0f(ξi) Δxi - I| < ε при любом ξi є [ xi ; xi+1] Тогда I = ∫abf(x)dx
:(по "Коши") Число I – называется определённым интегралом от f(x) на [ a ; b ], если для любого ε>0 существует δ=δ(ε)>0: для любого разбиения R отрезка [ a ; b ]: λR < δ, выполняется неравенство: |I- σR | = |∑n-1i=0f(ξi) Δxi - I| < ε при любом ξi є [ xi ; xi+1] Тогда I = ∫abf(x)dx
свойства Если функция интегрируема на [a; b], то она интегрируема на любом отрезке 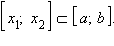
- Для любых a, b и c
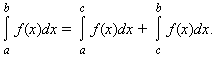 |
- Интеграл обладает свойством линейности: для любых функций f (x) и g (x) и любой постоянной A
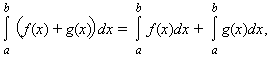 |
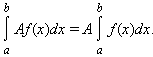 |
- Если f (x) и g (x) интегрируемы на [a; b], то f (x) · g (x) также интегрируема на этом отрезке.
- Если f (x) – периодическая функция с периодом T, то для любого a
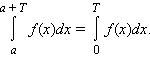 |
17. Понятие о дифференциальном уравнении: его порядке, общем и частном решении.
Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, 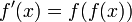 не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.
не является дифференциальным уравнением. Стоит также отметить, что дифференциальное уравнение может вообще не содержать неизвестную функцию, некоторые её производные и свободные переменные, но обязано содержать хотя бы одну из производных.
Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.
Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные 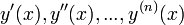 до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.
до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.
18. Дифференциальные уравнения первого порядка: с разделяющимися переменными.
Обыкновенное дифференциальное уравнение 1-го порядка (n=1) имеет вид: 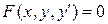 или, если его удается разрешить относительно производной:
или, если его удается разрешить относительно производной: 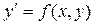 . Общее решение y=y(x,С) или общий интеграл
. Общее решение y=y(x,С) или общий интеграл 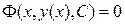 уравнения 1-го порядка содержат одну произвольную постоянную. Единственное начальное условие для уравнения 1-го порядка
уравнения 1-го порядка содержат одну произвольную постоянную. Единственное начальное условие для уравнения 1-го порядка 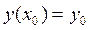 позволяет определить значение константы из общего решения или из общего интеграла. Таким образом, будет найдено частное решение или, что тоже, будет решена задача Коши. Вопрос о существовании и единственности решения задачи Коши является одним из центральных в общей теории обыкновенных дифференциальных уравнений. Для уравнения 1-го порядка, в частности, справедлива теорема, принимаемая здесь без доказательства.
позволяет определить значение константы из общего решения или из общего интеграла. Таким образом, будет найдено частное решение или, что тоже, будет решена задача Коши. Вопрос о существовании и единственности решения задачи Коши является одним из центральных в общей теории обыкновенных дифференциальных уравнений. Для уравнения 1-го порядка, в частности, справедлива теорема, принимаемая здесь без доказательства.
Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида 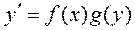
или уравнение вида 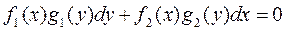
19. Линейные дифференциальные уравнения, однородные и неоднородные. Понятие общего решения линейного уравнения.
В математике линейное дифференциальное уравнение имеет вид
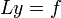
где дифференциальный оператор L линеен, y — неизвестная функция 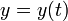 , а правая часть
, а правая часть 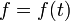 — функция от той же переменной, что и y.
— функция от той же переменной, что и y.
Линейный оператор L можно рассматривать в форме
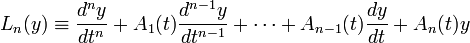
Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение 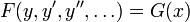 — однородно, если
— однородно, если 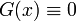 .
.
В случае, если 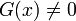 , говорят о неоднородном дифференциальном уравнении.
, говорят о неоднородном дифференциальном уравнении.
Неоднородное дифференциальное уравнение — дифференциальное уравнение (обыкновенное или в частных производных), которое содержит не равный тождественно нулю свободный член — слагаемое, не зависящее от неизвестных функций.
Общее решение диффференциального уравнения выражается в виде:
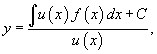
где C − произвольная постоянная.
20. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Рассмотрим линейное дифференциальное уравнение вида
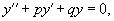
где p, q − постоянные коэффициенты.
Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение:
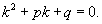
Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:
- Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией
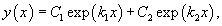
где C1 и C2 − произвольные действительные числа.
- Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид:
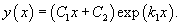
- Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде
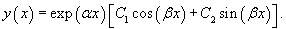
21. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод Лагранжа вариации произвольных постоянных.
Структура общего решения
Линейное неоднородное уравнение данного типа имеет вид:
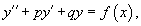
где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:
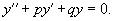
Теорема: Общее решение неоднородного уравнения является суммой общего решения y0(x) соответствуюшего однородного уравнения и частного решения y1(x) неоднородного уравнения:
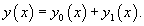
Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.
Метод вариации постоянных
Если общее решение y0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных.
Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:
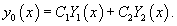
Вместо постоянных C1 и C2 будем рассматривать вспомогательные функции C1(x) и C2(x). Будем искать эти функции такими, чтобы решение
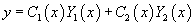
удовлетворяло неоднородному уравнению с правой частью f(x).
Неизвестные функции C1(x) и C2(x) определяются из системы двух уравнений:
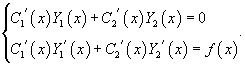
22. Числовой ряд. Сходимость и сумма ряда. Признак Даламбера.
Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).
Рассматриваются числовые ряды двух видов
- вещественные числовые ряды — изучаются в математическом анализе;
Сумма числового ряда 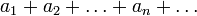 определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится[1]. Элементы ряда
определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится[1]. Элементы ряда 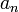 представляют собой либо вещественные, либо комплексные числа.комплексные числовые ряды — изучаются в комплексном анализе;
представляют собой либо вещественные, либо комплексные числа.комплексные числовые ряды — изучаются в комплексном анализе;
Признаки сходимости
Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости.
- Первая теорема Абеля: Пусть ряд
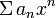 сходится в точке
сходится в точке 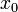 . Тогда этот ряд сходится абсолютно в круге
. Тогда этот ряд сходится абсолютно в круге 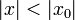 и равномерно по
и равномерно по 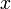 на любом компактном подмножестве этого круга.
на любом компактном подмножестве этого круга.
Обращая эту теорему, получаем, что если степенной ряд расходится при 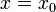 , он расходится при всех
, он расходится при всех 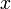 , таких что
, таких что 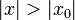 . Из первой теоремы Абеля также следует, что существует такой радиус круга
. Из первой теоремы Абеля также следует, что существует такой радиус круга 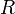 (возможно, нулевой или бесконечный), что при
(возможно, нулевой или бесконечный), что при 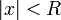 ряд сходится абсолютно (и равномерно по
ряд сходится абсолютно (и равномерно по 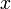 на компактных подмножествах круга
на компактных подмножествах круга 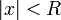 ), а при
), а при 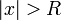 — расходится. Это значение
— расходится. Это значение 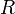 называется радиусом сходимости ряда, а круг
называется радиусом сходимости ряда, а круг 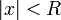 — кругом сходимости.
— кругом сходимости.
- Формула Коши-Адамара: Значение радиуса сходимости степенного ряда может быть вычислено по формуле:
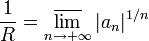
(По поводу определения верхнего предела 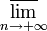 см. статью «Частичный предел последовательности».)
см. статью «Частичный предел последовательности».)
Пусть  и
и 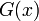 — два степенных ряда с радиусами сходимости
— два степенных ряда с радиусами сходимости 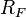 и
и 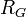 . Тогда
. Тогда
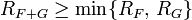
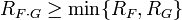
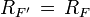
Если у ряда 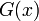 свободный член нулевой, тогда
свободный член нулевой, тогда
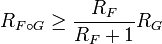
Вопрос о сходимости ряда в точках границы 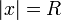 круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
- Признак Д’Аламбера: Если при
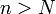 и
и 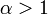 выполнено неравенство
выполнено неравенство
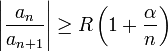
тогда степенной ряд 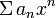 сходится во всех точках окружности
сходится во всех точках окружности 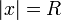 абсолютно и равномерно по
абсолютно и равномерно по 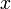 .
.
