Простейшие свойства линейной зависимости

1º. Система, содержащая нейтральный элемент, линейно зависима.

►Пусть система

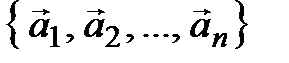(3.9)

содержит нейтральный элемент и пусть, например, 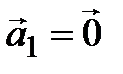. Положим

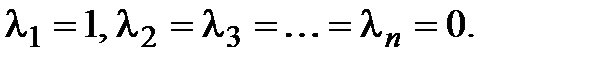(3.10)

Среди чисел (3.10) есть отличные от нуля и

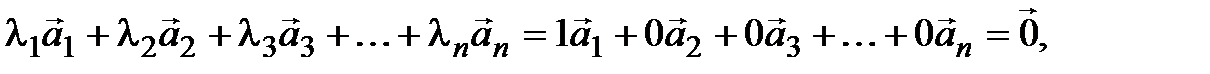
значит, система (3.9) линейно зависима. ◄

2º. Система, содержащая линейно зависимую подсистему, линейно зависима.

►Пусть система (3.9) содержит линейно зависимую подсистему и пусть, например, подсистема 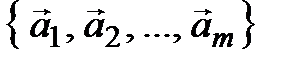при 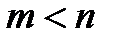линейно зависима. Это означает, что существуют числа

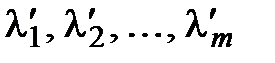, (3.11) не все равные 0, такие что 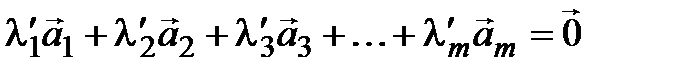. Положим

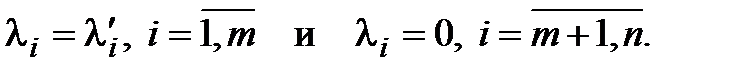(3.12)

Среди чисел (3.12) есть отличные от 0, так как таковые есть среди чисел (3.11), и

.

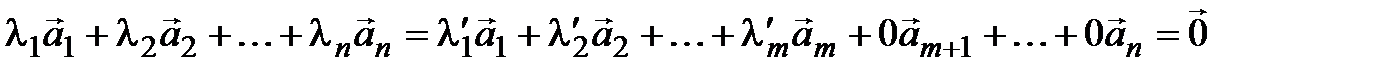Таким образом, исходная система линейно зависима. ◄

Следствие. Любая подсистема линейно независимой системы линейно независима.

3º. Критерий линейной зависимости. Для того чтобы система векторов была линейно зависимой, необходимо и достаточно, чтобы один из векторов можно было представить в виде линейной комбинации остальных.

►Необходимость. Дано: система 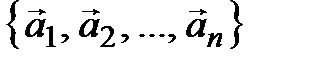линейно зависима. Значит, существуют числа 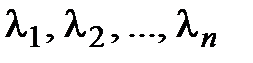, не все равные 0, такие, что справедливо равенство

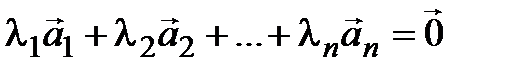. (3.13)

Пусть, например, 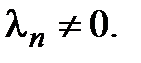Тогда из (3.13) можно выразить :

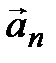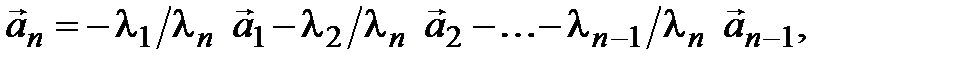
что и требовалось доказать.

Достаточность. Дано: один из векторов можно представить в виде линейной комбинации остальных, например, 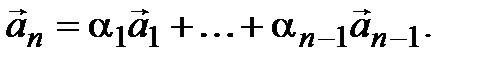Положим

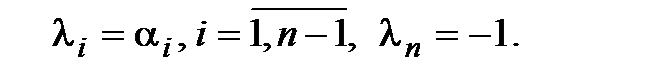(3.14)

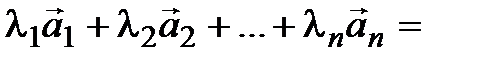
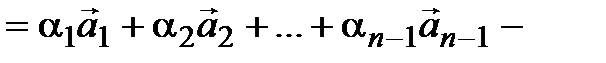
Cреди чисел (3.14) есть отличные от 0 и 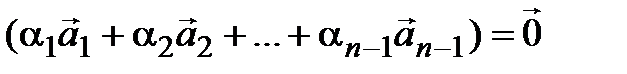, значит, исходная система линейно зависима. ◄

4º. Пусть система

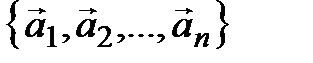(3.15)

линейно независима, а система

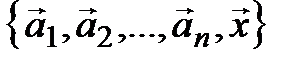– (3.16)

линейно зависима. Тогда 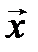можно представить в виде линейной комбинации элементов системы (3.15).

►В силу линейной зависимости системы (3.16) существуют числа 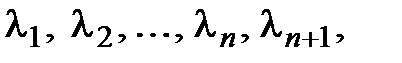не все равные 0, такие, что

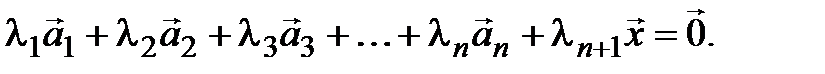(3.17)

Предположим, что 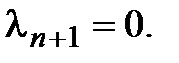Значит, среди чисел 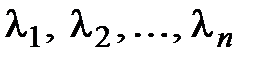есть отличные от нуля, и из (3.17) вытекает, что 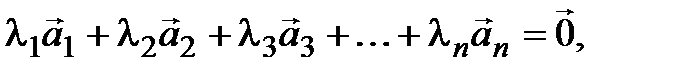что противоречит линейной независимости (3.15). Таким образом, 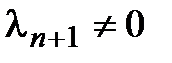, и из (3.17) получаем требуемое утверждение.◄

5º. Для того чтобы система из одного элемента была линейно зависимой, необходимо и достаточно, чтобы он был нулевым.

►Достаточность вытекает из первого свойства.

Необходимость.Пусть система 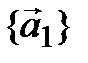линейно зависима, тогда существует число 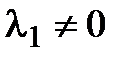такое, что 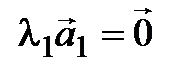. Значит, на основании 6-го следствия из аксиом (§1) .◄

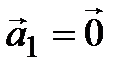Следующие свойства формулируем для пространства свободных векторов.

6º. Для того чтобы два вектора были линейно зависимыми, необходимо и достаточно, чтобы они были коллинеарными.

7º. Для того чтобы три вектора были линейно зависимыми, необходимо и достаточно, чтобы они были компланарными.

►Доказательство последних двух свойств вытекает из третьего свойства и критериев коллинеарности и компланарности из аналитической геометрии. ◄

Вопрос 3