Изучение механических затухающих колебаний

Цель работы: определить основные характеристики затухающих механических колебаний.

Приборы и принадлежности: специальная установка, снабженная секундомером, счетчиком числа колебаний и шкалой-линейкой.

Теоретические сведения

Всякое движущееся тело встречает сопротивление своему движе­нию со стороны окружающей его среды и других тел, с которыми оно во время движения соприкасается. Иначе говоря, на любое движущееся тело действуют силы трения. Природа этих сил может быть различной, но в результате их действия всегда происходит превращение механи­ческой энергии во внутреннюю энергию трущихся тел, т.е. в энергию теплового движения их частиц (диссипация энергии).

Силы трения довольно сложно зависят от скорости, но при колебаниях, когда скорость тела по абсолютной величине мала, можно счи­тать с достаточной степенью точности, что силы трения пропорциональ­ны скорости движения. Поэтому уравнение движения при колебаниях груза будет иметь следующий вид:

ma=-kx-rV, (8.1)

где m - масса колеблющегося тела; kx - упругая сила; rV - сила тре­ния; k - коэффициент упругости; х - смещение системы из положения равновесия; r - коэффициент трения, зависящий от свойств среды, фор­мы и размеров движущегося тела; V - скорость движения.

Заменив 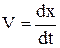и и 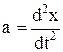перенеся все члены в уравнении (8.1) в левую часть, получим

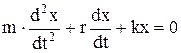(8.2)

Это уравнение носит название дифференциального уравнения свобод­ных колебаний в среде с линейным сопротивлением.

Решением уравнения (8.2) является следующая функция времени:

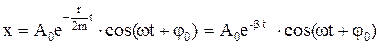(8.3)

Движение представляется произведением экспоненциальной функции (затухающей) 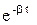на периодическую функцию соs(ωt+φ₀).

Величина β= r/2m называется коэффициентом затухания. Частота колебаний

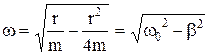(8.4)

называется собственной циклической частотой колебаний диссипативной системы, 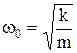- циклическая частота свободных незатухающих колебаний рассматриваемой системы в отсутствие сил трения.

Величину 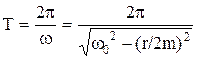(8.5)

называют условным периодом затухающих колебаний. Из формулы (8.5) видно, что период затухающих колебаний несколько больше периода колебаний той же системы в отсутствие затухания. Это связано с некоторым замедлением движения, которое обусловливают силы сопротивления. На рис. 8.1 приведен график затухающих колебаний.

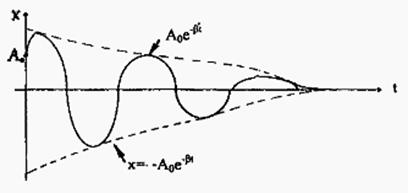
Рис. 8.1

Отношение амплитуд затухающего колебания, отстоящих друг от друга на интервал времени равный периоду, постоянно во все время колебаний,

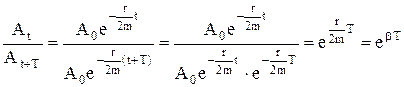, (8.6)

где β=r/2m называется коэффициентом затухания.

Коэффициент затухания определяет быстроту убывания амплитуды колебаний.

Логарифмический декремент затухания определяет число полных колебаний маятника за время затухания этих колебаний, т.е. логарифмический декремент затухания связан с добротностью периодичного движения маятника.

Натуральный логарифм этого отношения называется логарифмическим декрементом затухания

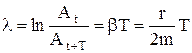(8.7)

Логарифмический декремент затухания, который характеризует бы­строту убывания амплитуды.

Если обозначить через τ промежуток времени, за который амплитуда колебаний уменьшится в е раз, тогда

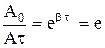(8.8)

откуда β_τ=1 или β=1/τ.

Следовательно, коэффициент затухания β есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Время τ называют временем релаксации.

Обозначив через N_e число полных колебаний, за которое амплитуда уменьшится в е раз, находим

τ =N_eT (8.9)

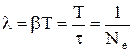(8.10)

Следовательно, логарифмический декремент затуханий δ есть физиче­ская величина, обратная числу колебаний N_e, по истечении которых ам­плитуда убывает в е раз. На основании соотношения (8.8) строим график (рис. 8.2).

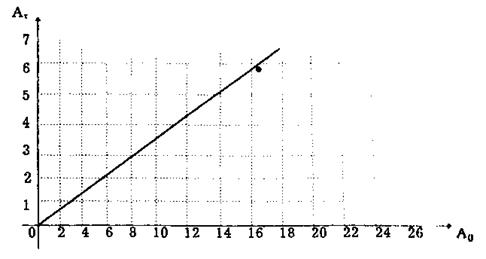
Рис. 8.2

На передней панели прибора (рис. 8.3) три клавиши: 1(сеть) -выключатель сети; 2(пуск) - запуск счетчика колебаний и секундомера; 2(стоп) - остановка счетчика колебаний и секундомера.

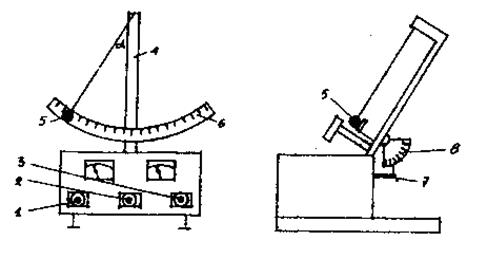
Рис. 8.3

На стойке 4 под­вешен металлический шарик 5. Амплитуду колебаний шарика измеря­ют по шкале 6. Установка позволяет определить характеристики зату­хающих колебаний при различных силах сопротивления. Для измене­ния силы сопротивления плоскость колебаний шарика ручкой 7 можно отклонить от вертикального положения на угол φ, который измеряют по шкале 8. Шарик, совершающий колебательные движения, начинает кататься по плоскости установки. Для отклоненной плоскости сила сопротивления складывается из двух сил: силы вязкого трения шарика в воздухе, зависящей от скорости, и постоянной силы трения качения.

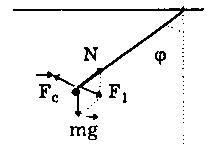Рис. 8.4

Следует отметить, что при отклонении от вертикали плоскости колебаний на угол φ изменяется период колебаний. Это связано с изменением квазиупругой силы F1 (рис. 8.4). В предель­ном случае, когда угол φ =90°, F1=-kx=0 , колебания совершаться системой не будут.

Порядок выполнения работы

1.Включить установку в сеть и проверить работу регистрирующих систем: электронного секундомера и счетчика числа колебаний.

2. Из рис.8.2 по начальной амплитуде определить амплитуду А_τ послед­него колебания, при котором начальная амплитуда уменьшится в е раз.
A_τ=A₀/e , число е ≈2,72

3. Отклонить шарик от положения равновесия на А₀. Определить число
колебаний N_e и время т, по истечении которого амплитуда уменьшится
и примет значение А_τ

4. По формулам λ=l/N_e; T=τ/N_e; β=1/τ; r=2βm вычислить
логарифмический декремент затухания, период колебаний, коэффициент затухания и коэффициент трения.

Опыты выполнить по 5 раз для двух значений угла наклона плоскости колебаний шарика 5°<<φ<15° и 20°<<φ<35°. Результаты измерений занести в таблицу.

Таблица

mшара=
φ	i	A0	Aτ	Ne	τi	λi	Ti	βi	ri
				< Ne>	< τi>	< λi>	< Ti>	< βi>	< ri>

Контрольные вопросы

1.Какие колебания называются свободными затухающими колебаниями?

2. От чего зависит сила сопротивления среды при движении тела в ней?

Какой физический смысл имеет коэффициент сопротивления среды?

3. Как записывают дифференциальное уравнение свободных затухающих колебаний, и уравнение зависимости смещения от времени?

4. Как зависит амплитуда затухающих колебаний от времени?

5. Каким соотношением связаны коэффициент затухания и логарифми-ческий декремент затухания?

6. Объяснить физический смысл коэффициента затухания и времени релаксации. Какая связь между ними?

7. Каким образом изменяются коэффициенты k и r , а также период колебаний системы Т при увеличении угла наклона плоскости колебаний?

8. Какие опытные данные нужно иметь для вычислений логарифмического декремента затухания и коэффициента сопротивления среды?

ЛАБОРАТОРНАЯ РАБОТА №9