Лекція 12. НЕВЛАСНІ ІНТЕГРАЛИ

12.1. Інтеграли з нескінченними межами (невласні інтеграли I роду)

Нехай функція 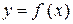визначена і неперервна при усіх значеннях х таких, що 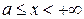. Розглянемо інтеграл 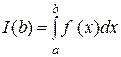. Цей інтеграл має смисл при усіх 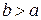. При зміні b інтеграл змінюється. Розглянемо питання про поведінку цього інтеграла при .

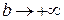Означення. Якщо існує скінченна границя 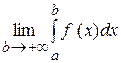, то ця границя називається невласним інтегралом від функції 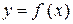на інтервалі 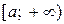і позначається так: .

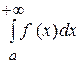Отже, за означенням маємо: .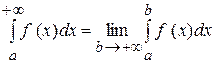

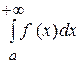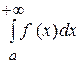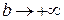Говорять, що в цьому випадку невласний інтеграл існує або збігається. Якщо при не має скінченної границі, то говорять, що невласний інтеграл не існує або розбігається.

Легко з'ясувати геометричний зміст невласного інтеграла у випадку, коли 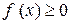: якщо інтеграл 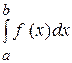виражає площу області, обмеженої кривою 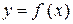, віссю абсцис і ординатами 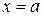, , 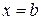то природно вважати, що невласний інтеграл 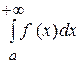виражає площу необмеженої (нескінченної) області, замкнутої між лініями 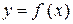, 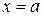і віссю абсцис.

Аналогічним чином означаються невласні інтеграли і від інших нескінченних інтервалів.

. .

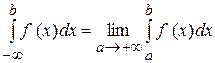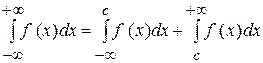Останню рівність варто розуміти так: якщо кожний із невласних інтегралів, який стоїть справа, існує, то існує (збігається) за означенням й інтеграл, який стоїть зліва.

Приклад 3.25. Обчислити невласні інтеграли:

а)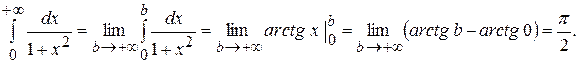

б) .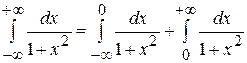

Другий інтеграл дорівнює 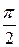. Обчислимо перший інтеграл.

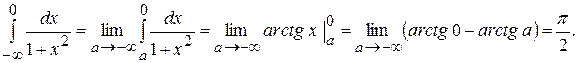
Отже, .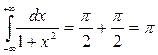

Приклад 3.26. Показати, для яких значень 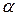інтеграл 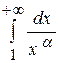збіжний, а для яких розбіжний.

Розв'язання.

При .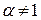

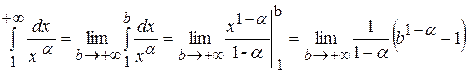Отже, щодо аналізованого інтеграла можна зробити такі висновки:

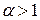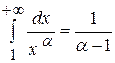якщо , то , тобто інтеграл збігається;

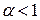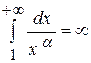якщо , то , тобто інтеграл розбігається.

При 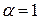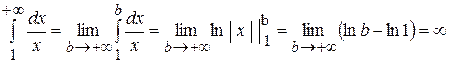, тобто інтеграл розбігається.

12.2. Інтеграл від необмеженої функції (невласні інтеграли II роду)

Нехай функція 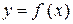визначена і неперервна при 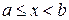, а при 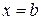функція або не визначена, або містить розрив. У цьому випадку не можна говорити про інтеграл 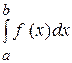як про границю інтегральних сум, тому що 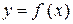не визначена на відрізку 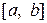, і тому ця границя може і не існувати.

Інтеграл 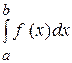від функції 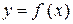, необмеженій в точці b, означається таким способом: .

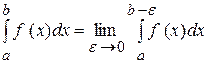Означення. Якщо границя, яка стоїть справа, існує, то інтеграл називають невласним збіжним інтегралом, інакше інтеграл називають розбіжним.

Якщо функція 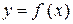необмежена в лівому кінці відрізка 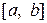(тобто при 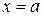), то за означенням .

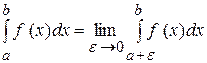Якщо функція 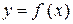необмежена в деякій точці 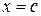, яка лежить усередині відрізка 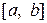, то 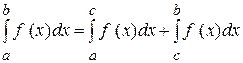, якщо обидва невласні інтеграли, які стоять у правій частині рівності, існують.

Приклад 3.27. Обчислити невласні інтеграли:

а)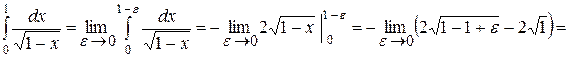

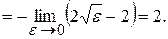
б)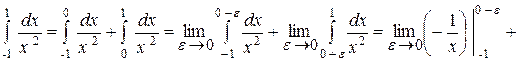

.

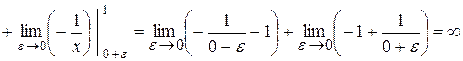Отже, даний інтеграл розбігається.

Зауваження. Якщо функція 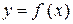, визначена на відрізку 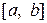, має всередині цього відрізка скінченне число точок розриву 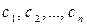, то інтеграл від функції 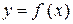на відрізку 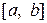означається так: 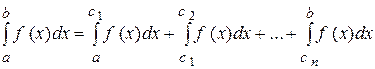, якщо кожний із невласних інтегралів у правій частині рівності збігається. Якщо ж хоча б один із цих інтегралів розбігається, то і 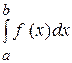називається розбіжним.

Багато прикладів зручніше розв’язувати, використовуючи умовну форму запису.

Приклад 3.28. Знайти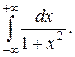

Розв'язання. 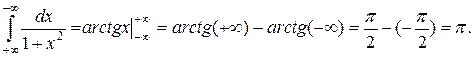Під записом, наприклад, 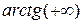мається на увазі .

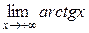Приклад 3.29.Знайти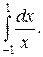

Розв’язання.Підінтегральна функція розривна в точці х = 0, що лежить усередині відрізка [-1;1]. За означенням,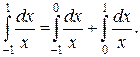

Обчислимо перший інтеграл. За означенням,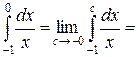

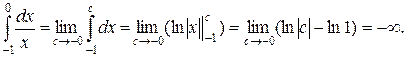
Тому що цей інтеграл розбігається, то розбігається і заданий інтеграл.

Зауваження. Якби ми не звернули увагу на те, що при 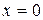функція 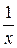розривна, і стали б обчислювати інтеграл за формулою Ньютона-Лейбніця, то одержали б помилковий результат.

Модуль IV. диференціальні рівняння. Ряди