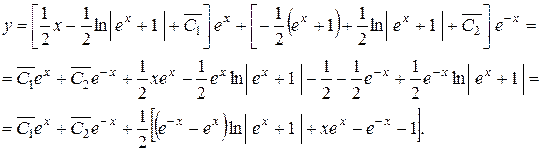Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами

Лінійним неоднорідним диференціальним рівнянням другого порядку зі сталими коефіцієнтами називається рівняння виду

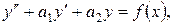(4.1)

де через 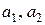, як і раніше, позначені відомі сталі коефіцієнти; 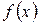- довільна задана функція.

Загальний розв’язок рівняння (4.1) 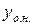може бути представлений у вигляді суми загального розв’язку відповідного однорідного рівняння 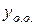і деякого частинного розв’язку неоднорідного рівняння 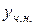, тобто

.

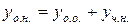Метод визначення загального розв’язку однорідного рівняння докладно описано в підрозділі 2.3.

Розглянемо тепер способи знаходження частинного розв’язку неоднорідного рівняння.

а) метод невизначених коефіцієнтів

Метод невизначених коефіцієнтів використовується лише для диференціальних рівнянь зі спеціальною правою частиною.

I випадок: Функція 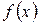- багаточлен степеня, тобто

.

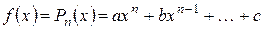Тоді

1) якщо число 0 (нуль) не є коренем характеристичного рівняння, то 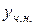шукаємо також у вигляді багаточлена степеня з невизначеними коефіцієнтами, тобто

,

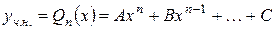(4.2)

де 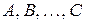- невідомі коефіцієнти, які належать визначенню;

2) якщо нуль є коренем характеристичного рівняння кратності 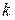( 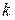може бути дорівнювати 1 або 2), то

.

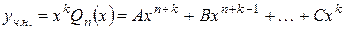(4.3)

Підставляючи для 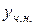(4.2) або (4.3) в початкове диференціальне рівняння (4.1) і прирівнюючи коефіцієнти при однакових степенях 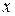, одержуємо систему лінійних алгебраїчних рівнянь для визначення невідомих коефіцієнтів .

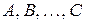Приклади. Знайти загальний розв’язок рівняння.

1.

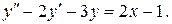
Так як 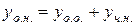, то розв’яжемо спочатку відповідне рівняння

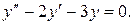
Характеристичне рівняння має вид

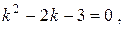його корені 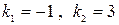. Отже,

.

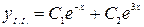Так як серед коренів характеристичного рівняння немає кореня 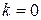, а права частина заданого рівняння представляє собою багаточлен першої степені, то 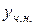шукаємо у вигляді

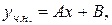
де 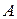і 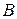- невідомі коефіцієнти.

Диференціюючи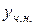

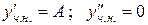
і підставляючи в початкове рівняння, маємо:

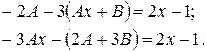
Прирівняємо коефіцієнти при однакових степенях 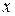в правій і лівій частині останнього рівняння:

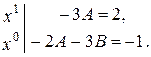
З першого рівняння знаходимо 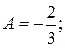із другого 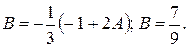Тоді 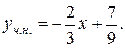Отже маємо:

.

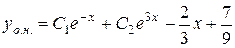2.

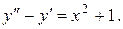
Як і раніше, знайдемо спочатку 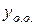, тобто розв’язуємо рівняння

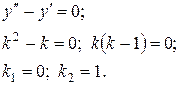
Тоді 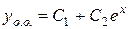. В даному рівнянні 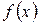- многочлен другого степеня. Враховуючи, що 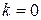- корінь характеристичного рівняння кратності 1, шукаємо 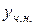у вигляді:

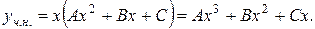
Далі знаходимо

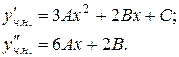
Підставимо в рівняння:

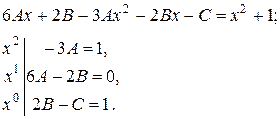
Тоді

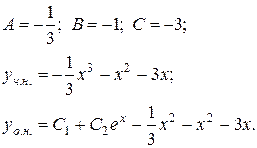
ІІ випадок: 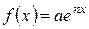( 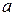- відома константа).

Тоді

1) число не є коренем характеристичного рівняння, то

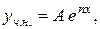
де 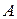- невідомий сталий коефіцієнт.

2) число - корінь характеристичного рівняння кратності 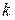, то

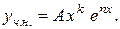
Приклади.

1. .

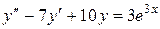Розв’язуємо однорідне рівняння:

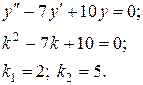
Отже,

.

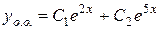В правій частині рівняння стоїть показникова функція 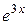, тобто тут 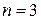. Так як 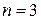не співпадає ні з одним із коренів характеристичного рівняння, то

.

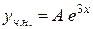Далі знаходимо невідомі константи як і раніше. Диференціюємо

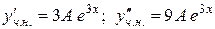
і підставляємо в рівняння:

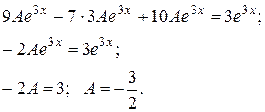
Отже,

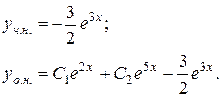
2.

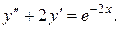
Знаходимо 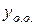, розв’язуючи однорідне рівняння

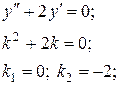
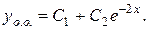
В правій частині заданого рівняння стоїть показникова функція, причому 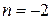співпадає з одним із коренів характеристичного рівняння 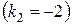. Тому необхідно шукати 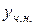у вигляді

.

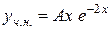Знаходимо:

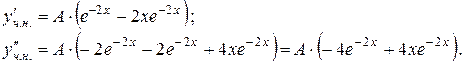
Підставляємо 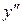і 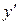в рівняння і визначаємо коефіцієнт :

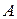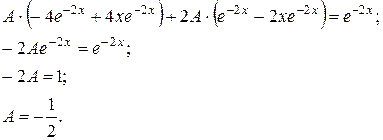
Звідси .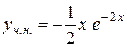

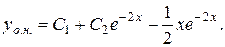
Ш випадок: 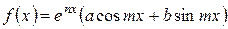( 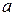і 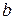- задані константи).

Тоді

1) якщо числа 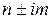( 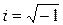- уявна одиниця) не є коренями характеристичного рівняння, то

,

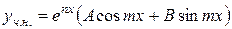де 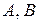- невідомі сталі, які необхідно визначити.

2) якщо числа 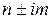- корені характеристичного рівняння, то

.

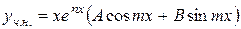Приклади.

1.

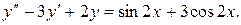
Записуємо відповідне однорідне рівняння і шукаємо його розв’язок:

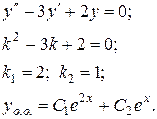
В даному рівнянні 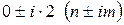не співпадають з коренями характеристичного рівняння ( 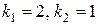- дійсні числа). Отже,

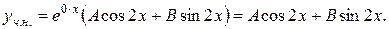
Далі знаходимо:

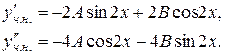
Після підстановки в рівняння

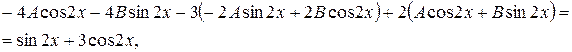
прирівнюючи коефіцієнти при однакових функціях, одержуємо систему рівнянь

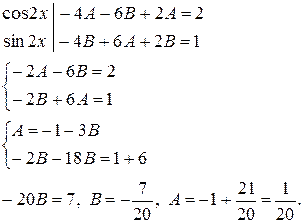
Отже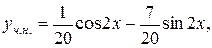

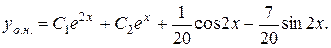
2.

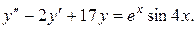
Однорідне рівняння має вид

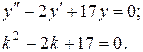
Визначаємо корені характеристичного рівняння:

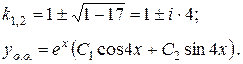
Порівнюючи корені характеристичного рівняння з числом 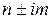(див. праву частину диференціального рівняння), бачимо, що вони співпадають:

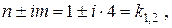
отже 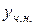необхідно знаходити у вигляді

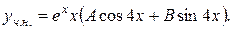
Визначимо значення сталих 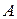і .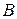

Для цього знаходимо

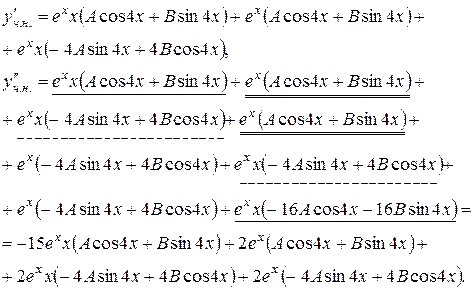
Підставляємо 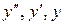в диференціальне рівняння:

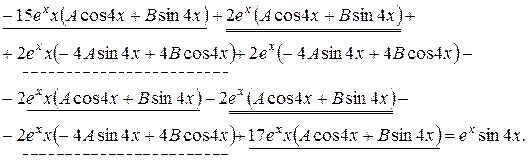
Приводимо подібні в даному виразі:

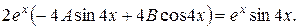
Прирівняємо коефіцієнти при однакових функціях:

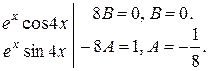
Тоді маємо:

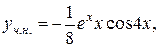
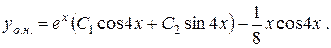
IV випадок: 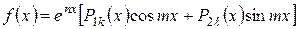, де 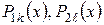- деякі багаточлени степеня 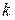і 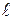відповідно.

Тоді

1) якщо числа 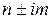не є коренями характеристичного рівняння, то

,

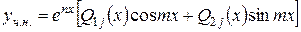де 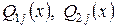- багаточлени з невизначеними коефіцієнтами степеня 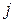, де 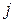- максимальне з чисел 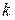і .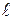

2) якщо 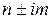- корені характеристичного рівняння, то

.

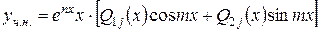Приклади.

1.

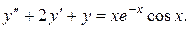
Однорідне рівняння має вид

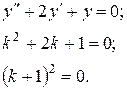
Тоді маємо 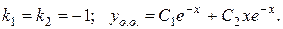Числа 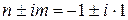не співпадають з коренями характеристичного рівняння, 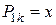- багаточлен першого степеня; 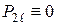, тому будемо шукати 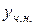у вигляді

,

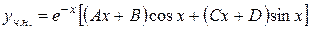де 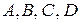- невідомі коефіцієнти.

Знаходимо :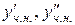

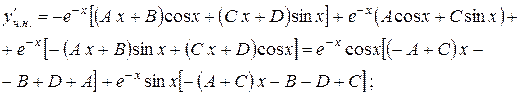
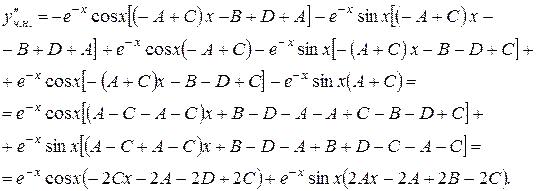
Підставляємо в рівняння:

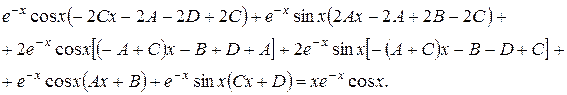
Спрощуючи вираз і приводячи подібні, маємо:

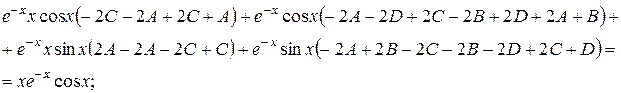
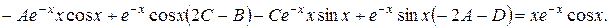
Прирівнюємо коефіцієнти при однакових функціях:

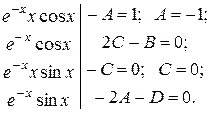
Маємо: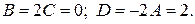

Таким чином,

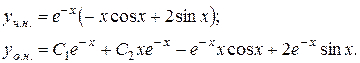
2.

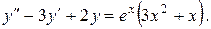
Запишемо однорідне рівняння

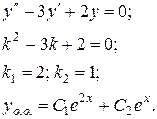
Вираз 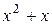представляє собою багаточлен другого степеня, а число 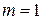є коренем характеристичного рівняння. Тоді

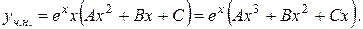
Знайдемо невідомі сталі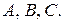

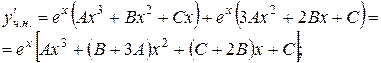
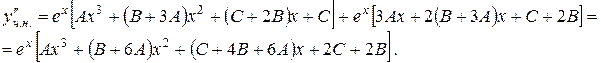
Після підстановки в диференціальне рівняння, маємо:

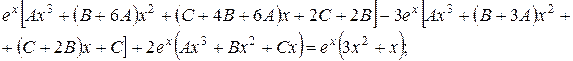
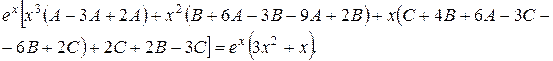
Після перетворень маємо:

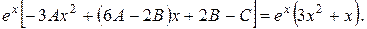
Прирівнюємо коефіцієнти при однакових степенях :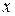

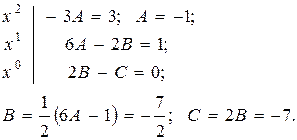
Таким чином

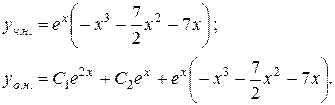
Зауваження. Якщо неоднорідне диференціальне рівняння має вид

,

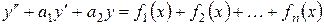(4.4)

тобто права частина представлена у вигляді суми функцій, причому відомі частинні розв’язки рівнянь

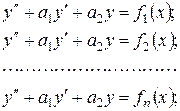
тобто відповідно функції 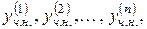то сума

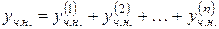(4.5)

є частинним розв’язком неоднорідного рівняння (4.4).

б) метод варіації довільних сталих

Метод варіації довільних сталих (метод Лагранжа) дозволяє находити загальний розв’язок неоднорідних диференціальних рівнянь, не накладаючи обмежень на вид правої частини, тобто є загальним методом інтегрування неоднорідних диференціальних рівнянь із сталими коефіцієнтами.

Нехай дано неоднорідне диференціальне рівняння

,

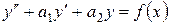(4.6)

де 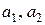- сталі коефіцієнти; 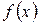- довільна функція.

Розглянемо відповідне однорідне рівняння 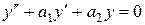. Його загальний розв’язок, як відомо, визначається досить просто і може бути представленим у вигляді лінійної комбінації двох лінійно незалежних частинних розв’язків 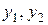, тобто

.

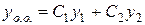(4.7)

Далі, будемо вважати у виразі (4.7) стал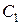і і 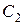функціями від 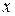, тобто шукати загальний розв’язок неоднорідного рівняння (4.6) у вигляді

,

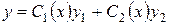(4.8)

де 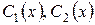- невідомі функції, які необхідно визначити.

В теорії диференціальних рівнянь показано, що визначення похідних від початкових функцій 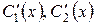зводиться до розв’язку лінійної алгебраїчної системи двох рівнянь з двома невідомими виду

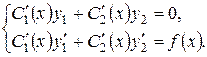(4.9)

Система лінійних алгебраїчних рівнянь сумісна і має єдиний розв’язок, якщо головний визначник системи

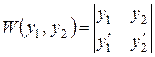- визначник Вронського – відмінний від нуля. Тоді вираз для 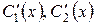в загальному вигляді буде наступним

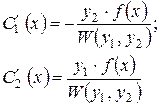(4.10)

Інтегруючи співвідношення (4.10), находимо вираз для початкових функцій :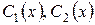

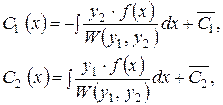(4.11)

де 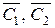- константи інтегрування.

Підставляючи у формулу (4.8) найдені вирази для 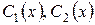(4.10), одержимо загальний розв’язок неоднорідного рівняння (4.6):

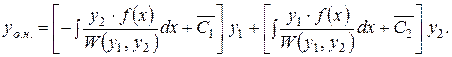(4.12)

Приклад. Знайти загальний розв’язок диференціального рівняння

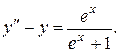
Запишемо відповідне однлрідне рівняння і найдемо його загальний розв’язок:

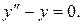
Характеристичне рівняння має вид

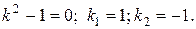
Таким чином, лінійно незалежними частинними розв’язками будуть функці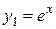ї і 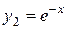, а загальний розв’язок однорідного рівняння

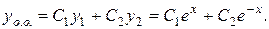
Загальний розв’язок початкового однорідного рівняння шукаємо у вигляді

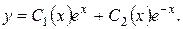
Система рівнянь (4.9) буде в даному випадку записана таким чином:

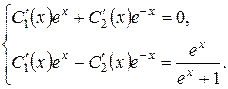
Додаючи рівняння, маємо:

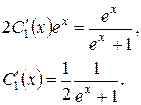
Інтегруючи останню рівність:

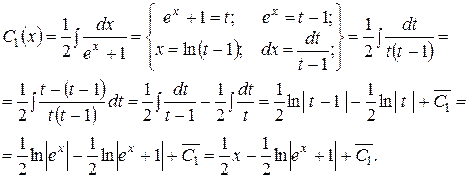
Із першого рівняння системи находимо:

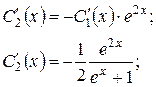
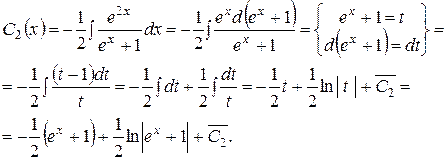
Загальний розв’язок в силу (4.12) має вид