Метод Кутта-Мерсона решения задачи Коши для ОДУ 1 порядка

Мерсон предложил модификацию метода Рунге-Кутта четвертого порядка, позволяющую оценивать погрешность на каждом шаге и принимать решение об изменении величины шага. Схема Мерсона выглядит следующим образом:

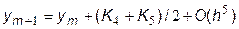(7.14)

где	K1 = h3 f(xm, ym), h3=h/3,
	K2 = h3 f(xm+h3, ym+K1),
	K3 = h f(xm+h3, ym+(K1+K2)/2),
	K4 = K1+ h3 f(xm+h/2, ym+0,375(K1+K3)),
	K5 = h3 f(xm+h, ym+1,5(K4 - K3)).

Эта схема требует на каждом шаге вычислять правую часть дифференциального уравнения в пяти точках, но она позволяет на каждом шаге определять погрешность решения R по формуле

R = 0,1(2K4 - 3K3 - K5).

(7.15)

Для автоматического изменения шага интегрирования рекомендуется следующий критерий. Если абсолютное значение величины R, вычисленное по формуле (7.15), на (m+1)-м шаге окажется больше допустимой заранее заданной погрешности 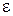, т.е.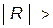 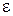, то шаг h уменьшается вдвое и вычисления по схеме (7.14) повторяются с точки (x_m,y_m). При выполнении условия 32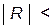 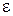шаг h можно удвоить начиная с точки (x_m+1,y_m+1).

Следует обратить внимание, что, если по условиям задачи требуется сохранять в памяти ЭВМ все вычисленные точки до конца решения, то, по сравнению с другими методами, здесь необходимо организовывать массив и для абсцисс точек, т.к. шаг изменения по оси OX - переменный.