Решение типового задания 21-30
Даны координаты вершин пирамиды 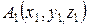 ,
, 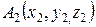 ,
, 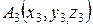 ,
, 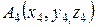 . Найти: 1). площадь грани
. Найти: 1). площадь грани 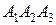 ; 2). объем пирамиды; 3). уравнения прямой
; 2). объем пирамиды; 3). уравнения прямой 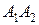 ; 4). уравнение плоскости
; 4). уравнение плоскости 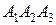 ; 5). уравнения высоты
; 5). уравнения высоты 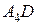 , опущенной из вершины
, опущенной из вершины 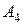 на грань
на грань 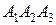 ; 6). длину высоты
; 6). длину высоты 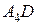 ; 7). координаты точки пересечения высоты
; 7). координаты точки пересечения высоты 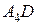 с плоскостью
с плоскостью 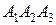 .
.
Например, A1(3;5;4), A2(6;9;4), A3(0;7;2), A4(2;3;7).
1) Для нахождения площади грани 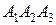 воспользуемся геометрическим смыслом модуля векторного произведения
воспользуемся геометрическим смыслом модуля векторного произведения 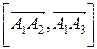 , равного площади параллелограмма, построенного на векторах
, равного площади параллелограмма, построенного на векторах 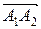
 и
и 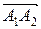 как на сторонах.
как на сторонах.
Найдем векторное произведение





Тогда искомая площадь грани 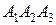 равна:
равна:
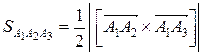 =
= 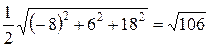 (ед2).
(ед2).
2) Объем пирамиды найдем, используя геометрический смысл модуля смешанного произведения 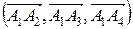 , равного объему параллелепипеда, построенного на векторах
, равного объему параллелепипеда, построенного на векторах 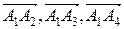 как на ребрах.
как на ребрах.
Вычислим смешанное произведение векторов 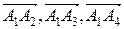 :
:
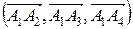 =
= 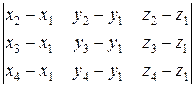 =
= 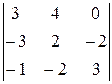 = 38.
= 38.
Так как объем пирамиды составляет шестую часть объема соответствующего параллелепипеда, то
Vпир = 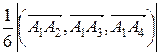 =
= 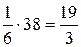 (ед3).
(ед3).
3) Чтобы найти уравнения прямой 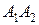 , используем уравнения прямой в пространстве, проходящей через две известные точки
, используем уравнения прямой в пространстве, проходящей через две известные точки 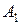 и
и 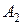
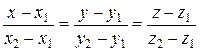 .
.
Уравнения прямой 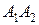 принимают вид:
принимают вид:
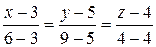 или
или 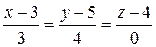 .
.
4) Для получения уравнения грани 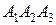 используем уравнение плоскости, проходящей через три данные точки
используем уравнение плоскости, проходящей через три данные точки 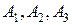 :
: 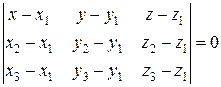 .
.
В нашей задаче: 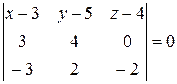 .
.
Определитель вычислим методом разложения по элементам первой строки.
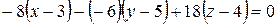 , раскрыв скобки, и приведя подобные, получаем – 8x + 6y + 18z – 78 = 0, сократив на (–2), искомое уравнение будет иметь вид 4x – 3y – 9z + 39 = 0.
, раскрыв скобки, и приведя подобные, получаем – 8x + 6y + 18z – 78 = 0, сократив на (–2), искомое уравнение будет иметь вид 4x – 3y – 9z + 39 = 0.
5) Чтобы найти уравнения высоты, опущенной из вершины А4 на грань 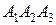 , используем канонические уравнения прямой в пространстве, проходящей через известную точку А4 с направляющим вектором
, используем канонические уравнения прямой в пространстве, проходящей через известную точку А4 с направляющим вектором 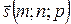
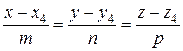 .
.
Так как высота перпендикулярна грани 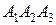 , то в качестве направляющего вектора
, то в качестве направляющего вектора 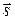 можно использовать нормальный вектор плоскости
можно использовать нормальный вектор плоскости 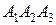 , координатами которого являются коэффициенты при
, координатами которого являются коэффициенты при 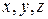 в полученном уравнении грани
в полученном уравнении грани 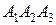 :
: 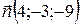 .
.
Итак, уравнения высоты примут вид:
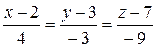 .
.
6) Для вычисления длины высоты 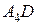 примем формулу расстояния от точки
примем формулу расстояния от точки 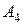 до плоскости
до плоскости 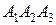 .
.
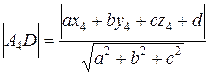 ,
,
где 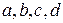 – коэффициенты и свободный член из уравнения плоскости
– коэффициенты и свободный член из уравнения плоскости 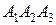 .
.
Таким образом,
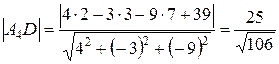 .
.
Координаты точки пересечения высоты 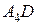 с плоскостью
с плоскостью 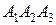 получаются как результат решения системы, составленной из уравнения грани
получаются как результат решения системы, составленной из уравнения грани 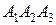 и уравнений высоты
и уравнений высоты 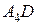 .
.
Запишем уравнения высоты 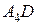 в параметрической форме:
в параметрической форме:
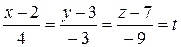 ,
,
где t – параметр, тогда 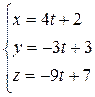 . Решая систему
. Решая систему 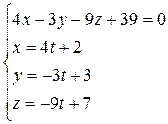 ,
,
найдем значение параметра t. Подставляя выражения 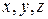 в первое уравнение, получим
в первое уравнение, получим
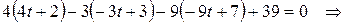
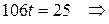
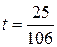 .
.
Искомые координаты точки пересечения:
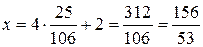 ;
; 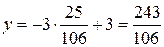 ;
; 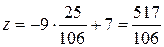 .
.
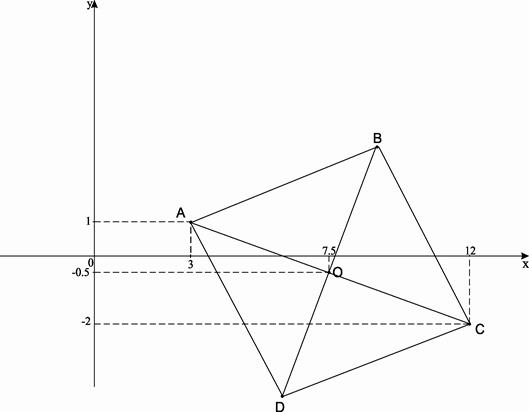
Решение задания типа 31-40 со следующим условием:
Известны уравнения двух сторон ромба 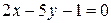 и
и 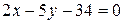 и уравнение одной из его диагоналей
и уравнение одной из его диагоналей 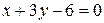 . Найти уравнение второй диагонали. Сделать чертеж.
. Найти уравнение второй диагонали. Сделать чертеж.
Решение.

Пусть 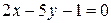 - уравнение стороны АВ. Так как прямые
- уравнение стороны АВ. Так как прямые 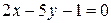 и
и 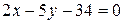 имеют одинаковые нормальные векторы
имеют одинаковые нормальные векторы 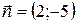 , следовательно, они параллельны. Поэтому
, следовательно, они параллельны. Поэтому 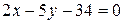 - уравнение противоположной стороны DC. Одна из диагоналей, например, АС имеет уравнение
- уравнение противоположной стороны DC. Одна из диагоналей, например, АС имеет уравнение 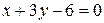 . Вершина ромба A является точкой пересечения прямых АВ и АС, следовательно ее можно найти, решив систему уравнений:
. Вершина ромба A является точкой пересечения прямых АВ и АС, следовательно ее можно найти, решив систему уравнений:
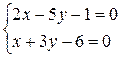 , откуда А(3;1).
, откуда А(3;1).
Вершину ромба С получим решением системы, составленной из уравнения прямых DC и АС:
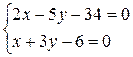 , откуда С(12;-2).
, откуда С(12;-2).
Точка О пересечения диагоналей является серединой отрезка АС, поэтому ее координаты можно найти по формулам:
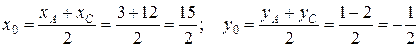 . Таким образом
. Таким образом 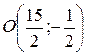 .
.
Так как диагонали ромба перпендикулярны, то угловой коэффициент искомой диагонали 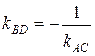 . Угловой коэффициент прямой АС
. Угловой коэффициент прямой АС 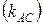 , найдем из ее уравнения:
, найдем из ее уравнения: 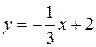 , откуда
, откуда 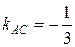 . Следовательно,
. Следовательно, 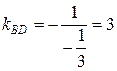 .
.
Уравнение диагонали BD найдем, зная угловой коэффициент 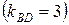 и точку
и точку 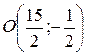 , лежащую на ней:
, лежащую на ней: 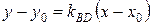 , т.е.
, т.е. 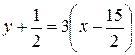 или
или 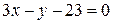 .
.
Ответ: 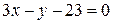 .
.
Выполним чертеж: