Дәріс сабағы. Туындының көмегімен функцияларды зерттеу және графигін салу

Функцияның өсуі мен кемуі. 1-анықтама. Егер 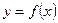функциясының анықталу облысында жатқан 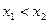элементтері үшін 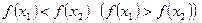теңсіздігі орындалса, онда ол өспелі (кемімелі) функция деп аталады.

2-анықтама.Егер 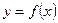функциясының анықталу облысында жатқан 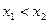элементтері үшін 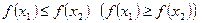теңсіздігі орындалса, онда ол кемімейтін (өспейтін) функция деп аталады.

Өспелі, кемімелі және өспейтін, кемімейтін функцияларды бірсарынды функциялар деп атайды.

Функцияның өсуі мен кемуінің қажетті және жеткілікті шарттары:

1. Егер дифференциалданатын 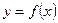функциясы 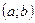интервалында өспелі (кемімелі) болса, онда оның осы интервалдағы туындысы теріс (оң) болмайды, яғни .

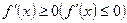2. Егер 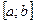сегментінде үзіліссіз және 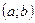интервалында дифференциалданатын 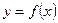функциясының осы интервалдың әрбір нүктесінде туындысы оң (теріс) болса, яғни 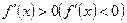болса, онда 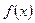функциясы сол интервалда өседі (кемиді).

3-анықтама. Функцияның туындысы нөлге тең немесе болмайтын нүктелерді функцияның күдікті нүктелері деп атайды.

Мысал. Функцияның бірсарынды (монотонды) болу интервалдарын және күдікті нүктелерін табыңдар: .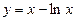

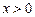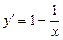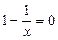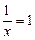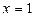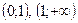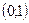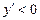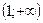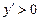Анықталу облысы: . , , , - күдікті нүкте, бұл нүкте анықталу облысын интервалдарына бөледі. Осы интервалдағы туынды таңбасын тексереміз: интервалында , яғни функция кемиді. -де , яғни функция өседі.

Функцияның экстремумы. 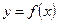функциясы 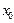нүктесін қамтитын интервалда үзіліссіз болсын.

4-анықтама. Егер 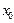нүктенің аймағындағы барлық 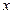үшін 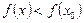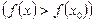теңсіздігі орындалса, онда 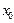нүктесі 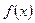функциясының максимум (минимум) нүктесі деп аталады. Максимум (минимум) нүктелеріндегі функцияның мәні сәйкес функцияның максимумы (минимумы) немесе қысқаша функцияның экстремумы деп аталады.

Функцияның экстремумы бар болуының қажетті шарты:

Егер дифференциалданатын 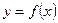функциясының 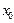нүктеде экстремумы бар болса, онда 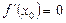немесе бұл нүктеде туындысы болмайды.

Мысал. 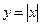, 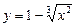функциялары 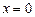нүктесінде сәйкес 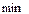және 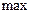мәндерін қабылдайды, ал бірақ бұл нүктеде олардың туындысы жоқ.

Функцияның экстремумы бар болса, онда ол тек қана күдікті нүктелерде болады. Кері тұжырым дұрыс емес, күдікті нүктелердің кез келгенінде экстремум бола бермейді.

Мысал. 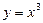, , 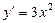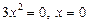. Бұл күдікті нүктеде оның эктремумы жоқ, себебі: 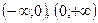интервалдарында .

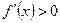Функция графигіне оның экстремум нүктесінде жүргізілген жанама 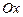өсіне параллель болады.

Функцияның экстремумы бар болуының жеткілікті шарттары:

1. Егер функцияның бірінші туындысы 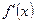бар болып, ол солдан оңға қарай күдікті 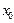нүктеде таңбасын плюстен минусқа өзгертетін болса, онда 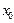нүктесі максимум нүктесі, ал егер – минустан плюске өзгертсе, онда 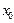нүктесі минимум нүктесі болады (1-сурет).

Ескерту. 1. Егер күдікті нүктеден өткенде 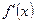-тің таңбасы өзгермесе, онда бұл нүктеде 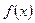функциясының экстремумы болмайды.

2. Күдікті нүктеден өткенде функция таңбасын өзгерткенмен қатар осы нүктеде функцияның үзіліссіз екендігіне көз жеткізу қажет.

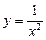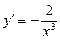
Мысал. , 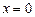нүктесінен солдан оңға қарай өткенде 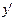өзінің таңбасын «+» тен «-»-ке өзгертеді, ал бірақ бұл нүктеде 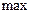жоқ. Өйткені, 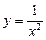функциясы бұл нүктеде үзілісті, яғни .

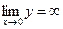2. Егер 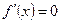теңдеуінің түбірі 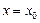және 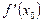бар болып, 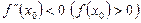болса, онда осы күдікті нүктеде функцияның максимумы (минимумы) бар болады.

Мысал. 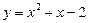функциясын экстремумға зерттеу керек.

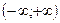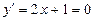
Шешуі. Анықталу облысы: . . 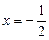. 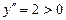Ендеше, 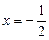нүктеде функция минимум мәнін қабылдайды: .

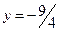3. Егер 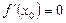, 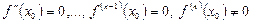делік. Егер 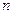-жұп сан және 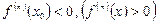болса, онда 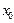нүктеде функцияның максимумы (минимумы) бар болады. Ал егер 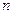-тақ сан болса, онда функцияның эктремумы болмайды.

Максимум, минимум анықтамаларында функцияның мәні тек 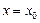нүктесіне «көрші» нүктелеріндегі мәндерінен ең үлкен (кіші) болатыны ғана айтылған. Сондықтан, берілген интервалда функцияның бірнеше экстремумы болуы мүмкін. Кейде қайсы бір минимум басқа бір максимумнан үлкен болуы мүмкін. Сондықтан, жеке экстремумдарды жергілікті (локальды) экстремум деп атайды. Ал аралықтағы ең үлкен, ең кіші мәндерін сәйкес түрде абсолюттік максимум, абсолюттік минимум деп те атайды.

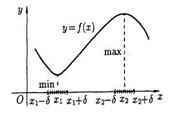
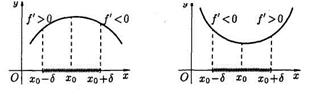
1-сурет 2-сурет

Функцияның кесіндідегі ең үлкен және ең кіші мәндері. 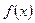функциясы 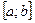кесіндісінде үзіліссіз функция болсын. Онда ол осы сегменттің шеткі (Вейерштрасстың 2-нші теоремасы бойынша) немесе ішкі нүктелерінде өзінің ең үлкен және ең кіші мәндерін қабылдайды. Егер ең үлкен (ең кіші) мәнін сегменттің ішкі нүктесінде қабылдаса, онда ол осы функцияның максимумдарының (минимумдарының) бірі болады.

Сонымен, функцияның 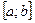сегменттегі ең үлкен, ең кіші мәндерін табу үшін:

1) Функцияның барлық күдікті нүктелерін табамыз;

2) Функцияның осы күдікті және шеткі нүктелердегі 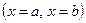мәндерін есептейміз;

3) Осы табылған мәндерді салыстырып, олардың ең үлкенін функцияның ең үлкен мәні, ең кішісін-функцияның ең кіші мәні деп аламыз.

Ескерту. Егер функцияның 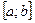сегментінде күдікті нүктелері болмаса, онда функция бұл аралықта өседі немесе кемиді. Ендеше, функция ең үлкен (М) мәнін кесіндінің бір ұшында, ең кіші мәнін ( 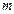) екінші ұшында қабылдайды.

Мысал. 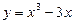функциясының 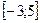сегментіндегі ең үлкен және ең кіші мәндерін табыңыз.

Шешуі. 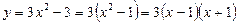. Осыдан 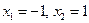-күдікті нүктелер. Олар берілген кесіндіде жатады. Функцияның осы күдікті және шеткі нүктелеріндегі мәндерін табамыз: 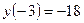, , 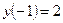, 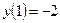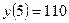. Осы мәндерді салыстырып, функцияның ең үлкен және ең кіші мәндерін анықтаймыз: у_{ең үлкен}(5)=110, у_{ең кіші}(-3)= -18.