Знайти ранг матриць
1. . 2. .
3. . 4. .
Відповіді. 1. 2. 2. 2. 3. 3. 4. 3.
1.15.Лінійна залежність та лінійна незалежність рядків (стовпців) матриці
Зупинимось ще на відомому вже в 1.14. прикладі матриці
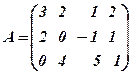 .
.
Там було встановлено, що ранг 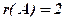 . Це означає, що один з рядків (стовпців) може бути записаний у вигляді лінійної комбінації двох інших. Для цього позначимо рядки матриці
. Це означає, що один з рядків (стовпців) може бути записаний у вигляді лінійної комбінації двох інших. Для цього позначимо рядки матриці 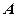 :
:
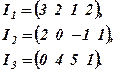
Покажемо, що можна знайти числа 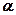 і
і 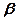 такими, що
такими, що
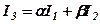 . (1)
. (1)
Дійсно, підставивши в (1) вирази для 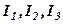 маємо:
маємо:
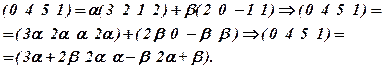
Відомо, що два рядки рівні, якщо в них рівні відповідні елементи, тобто
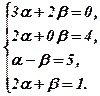 (2)
(2)
Із системи (2) знаходимо: 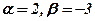 . Таким чином,
. Таким чином,
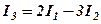 ,
,
або ще будемо говорити, що рядок 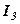 є лінійною комбінацією рядків
є лінійною комбінацією рядків 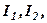 або ж рядок
або ж рядок 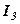 лінійно залежить від рядків
лінійно залежить від рядків 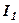 і
і 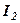 .
.
Перейдемо до означення понять лінійної залежності і лінійної незалежності рядків (стовпців) матриці 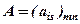 в загальній формі.
в загальній формі.
Нехай
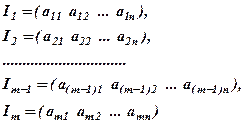
– рядки матриці 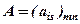 , і нехай
, і нехай
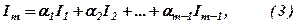
де 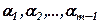 – деякі числа. Будемо говорити, що
– деякі числа. Будемо говорити, що 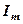 , тобто
, тобто
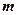 -ий рядок матриці
-ий рядок матриці 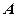 , лінійно виражаєтьсячерез перші
, лінійно виражаєтьсячерез перші 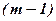 рядки цієї матриці, або що
рядки цієї матриці, або що 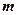 -ий рядок є лінійною комбінацією рядків
-ий рядок є лінійною комбінацією рядків 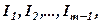 або ж, що рядок
або ж, що рядок 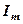 лінійно залежитьвід рядків
лінійно залежитьвід рядків 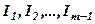 .
.
Рівність (3) можна переписати у вигляді
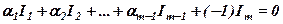 ,
,
де нуль в правій частині означає нульовий рядок.
Означення. Рядки 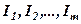 матриці
матриці 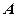 називаються лінійно залежними, якщо існують такі числа
називаються лінійно залежними, якщо існують такі числа 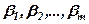 , не рівні одночасно нулю, що
, не рівні одночасно нулю, що
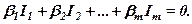 (4)
(4)
Якщо ж рівність (4) виконується тільки за умови, що всі коефіцієнти 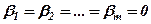 , то рядки
, то рядки 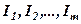 називаються лінійно незалежними.
називаються лінійно незалежними.
Ми вже відмічали, що якщо один з рядків матриці лінійно виражається через інші, то вони лінійно залежні. Навпаки, якщо має місце лінійна залежність (4) і при цьому хоча б один з коефіцієнтів, наприклад, 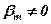 , то
, то
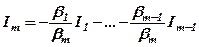 ,
,
тобто 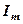 лінійно виражається через
лінійно виражається через 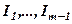 .
.
Аналогічним чином можна ввести поняття лінійної залежності і лінійної незалежності стовпців матриці 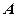 .
.
Теорема (про лінійну залежність і лінійну незалежність).
Якщо ранг матриці 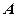 дорівнює
дорівнює 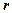 , то в цій матриці можна знайти
, то в цій матриці можна знайти 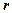 лінійно незалежних між собою рядків (стовпців), через які лінійно виражаються всі інші її рядки (стовпці).
лінійно незалежних між собою рядків (стовпців), через які лінійно виражаються всі інші її рядки (стовпці).
Наслідок 1. Максимальне число лінійно незалежних стовпців матриці дорівнює максимальному числу лінійно незалежних рядків, тому що при транспонуванні матриці її рядки стають стовпцями, а ранг при цьому не міняється.
Наслідок 2. Для того, щоб визначник дорівнював нулю, необхідно і досить, щоб його рядки (стовпці) були лінійно залежними.
1.16. Умови сумісності системи лінійних рівнянь. Теорема Кронекера – Капеллі[3]
Дослідимо в загальному вигляді систему 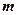 лінійних рівнянь з
лінійних рівнянь з 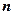 невідомими
невідомими 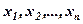 (
( 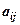 – задані коефіцієнти):
– задані коефіцієнти):
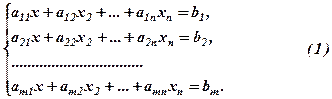
Розв’язком системи (1) називається сукупність чисел 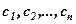 , яка будучи підставленою в кожне з рівнянь цієї системи замість невідомих
, яка будучи підставленою в кожне з рівнянь цієї системи замість невідомих 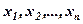 , перетворює її в тотожність.
, перетворює її в тотожність.
Система вигляду (1) називається сумісною, якщо вона має хоча б один розв’язок. Якщо система (1) не має розв’язку, то вона називається несумісною. Питання сумісності або несумісності системи можна розв’язати за допомогою ранга матриці.
Розглянемо матриці:
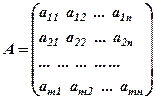 ,
, 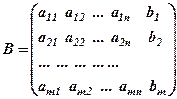 .
.
Матриця 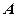 називається основною або матрицеюсистеми (1),
називається основною або матрицеюсистеми (1), 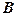 – розширеною матрицею. Позначимо їх ранги
– розширеною матрицею. Позначимо їх ранги 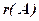 і
і 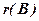 . Відмітимо, що
. Відмітимо, що 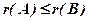 , тому що елементи матриці
, тому що елементи матриці 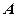 містяться серед елементів матриці
містяться серед елементів матриці 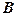 .
.
Умови сумісності чи несумісності системи лінійних рівнянь (1) виражаються наступною теоремою.
Теорема 1. (Кронекера – Капеллі). Для того щоб система лінійних рівнянь (1) було сумісною, необхідно і досить, щоб ранг матриці системи 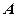 дорівнював рангу розширеної матриці
дорівнював рангу розширеної матриці 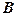 , тобто
, тобто 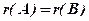 .
.
Із теореми випливає, що якщо 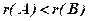 , то система несумісна.
, то система несумісна.
Сумісна система може мати єдиний розв’язок і тоді вона називається визначеною, або система може мати нескінченне число розв’язків і тоді вона називається невизначеною.
Теорема 2. Сумісна система (1) має єдинийрозв’язок, якщо 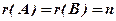 (ранги дорівнюють числу невідомих); якщо
(ранги дорівнюють числу невідомих); якщо 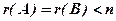 , то система має нескінченне число розв’язків.
, то система має нескінченне число розв’язків.
Вправи. Дослідити кожну із систем рівнянь і у випадку сумісності розв’язати її:
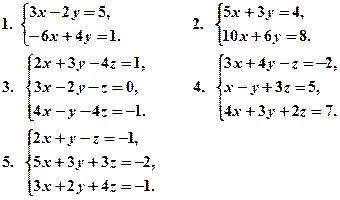
Відповіді: 1. Система несумісна. 2. Система має нескінченне число розв’язків, загальний розв’язок 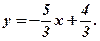 3. (1, 1, 1). 4. Система несумісна.
3. (1, 1, 1). 4. Система несумісна.
5. Система має нескінченне число розв’язків, загальний розв’язок: 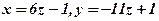 .
.
[1] К..Гаусс(1777-1855)-німецький математик,фізик,астроном
[2] Г. Крамер (1704 - 1752) - швейцарський математик.
[3] Л. Кронекер (1823 – 1891) – німецький математик,
А. Капеллі (1855 – 1910) – італійський математик.
