Дифференцирование и интегрирование сигнала
Дифференцирование сигнала 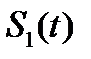 можно трактовать как почленное дифференцирование всех гармонических составляющих, входящих в его спектр. Но производная функции
можно трактовать как почленное дифференцирование всех гармонических составляющих, входящих в его спектр. Но производная функции 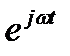 равна
равна 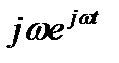 из чего непосредственно вытекают следующие соответствия:
из чего непосредственно вытекают следующие соответствия:
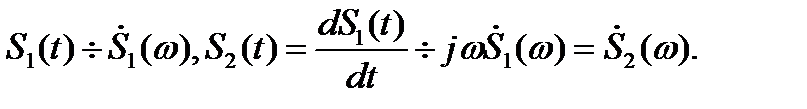
(2.16)
При дифференцировании скорость изменения сигнала во времени возрастает. Как следствие модуль спектра производной имеет большие значения в области высоких частот по сравнению с модулем спектра исходного сигнала.
В случае спектра производной 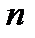 - го порядка
- го порядка
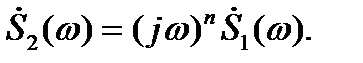
Дифференцирование сигнала по времени эквивалентно простой алгебраической операции умножения спектральной плотности на множитель 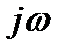 . Поэтому принято говорить, что мнимое число
. Поэтому принято говорить, что мнимое число 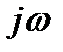 является оператором дифференцирования, действующим в частотной области.
является оператором дифференцирования, действующим в частотной области.
Сигнал 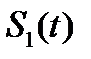 является первообразной (неопределённым интегралом по отношению
является первообразной (неопределённым интегралом по отношению 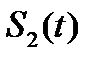 ).
).
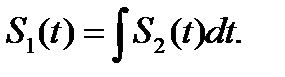
Из (2.16) формально следует, что спектр первообразной
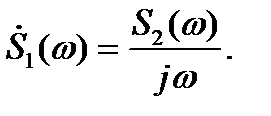 (2.17)
(2.17)
Таким образом, множитель 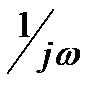 служит оператором интегрирования в частотной области.
служит оператором интегрирования в частотной области.
