Біртекті дифференциалдық теңдеулер

Анықтама. f(x, y) функциясы өзінің х және у аргументтеріне қатысты n-өлшемді біртекті делінеді, егер кез келген t параметрдің (нөлден өзге) мәні үшін келесі тепе-теңдік орындалатын болса:

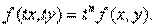
Мысал. Функция біртекті бола ма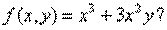

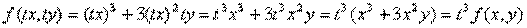
Сонымен f(x, y) функциясы 3-ші ретті біртекті болады.

Анықтама. Егер 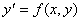түріндегі дифференциалдық теңдеудің оң жағы f(x, y) функциясы өзінің х және у аргументтеріне қатысты нөлдік өлшемді біртекті функция болса, онда теңдеу біртектіделінеді.

Егер P(x, y) және Q(x, y) функциялары – бірдей өлшемді біртекті функциялар болса, онда 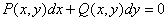теңдеуі біртекті болады.

Анықтама. 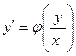түріндегі теңдеу біртекті дифференциалдық теңдеу деп аталады.

Мұндай теңдеуді шешу үшін 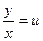алмастыруын жасап айнымалылары ажыратылған дифференциалдық теңдеулерге келтіреміз.

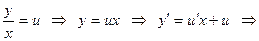
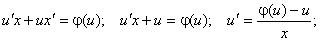
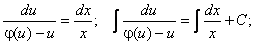
Интегралды таба отырып, u функциясының орнына х және у арқылы өрнектелген мәнін алмастырып, біртекті теңдеудің жалпы шешімін аламыз.

Мысал 1: 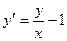- біртекті дифференциалдық теңдеуді шеш.

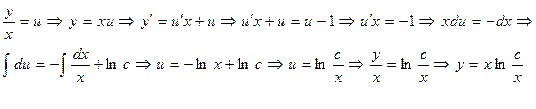
Мысал 2:

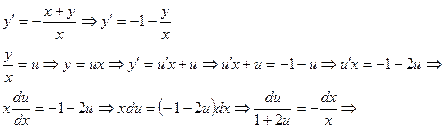
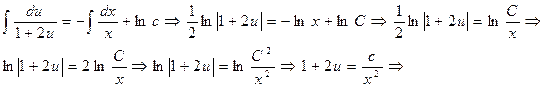
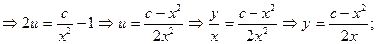
Мысал 3: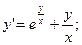

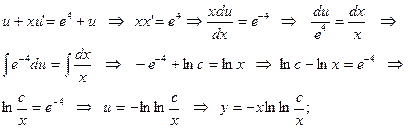
Біртектіге келтірілетін дифференциалдық теңдеулер

Мұндай теңдеулерге 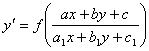түріндегі теңдеулер жатады.

1) Егер анықтауыш 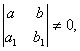онда

алмастыруын енгіземіз, мұндағы a және b сандары- 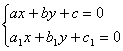жүйесінің шешімдері.

Мысал. 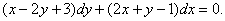теңдеуін шеш.

Шешуі.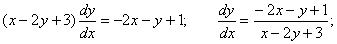

Анықтауышты есептейік: .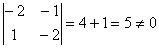

Нөлге тең емес болғандықтан келесі жүйені шешеміз:

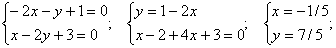
Ендеше алмастыруымыз 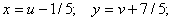түрінде болады, оны алғашқы теңдеуге қоямыз:

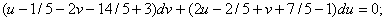
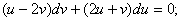
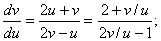
Айнымалыларды алмастырайық: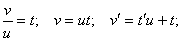

Жоғарғы теңдеуге қойсақ:

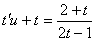
Айнымалыларды ажыратайық: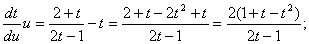

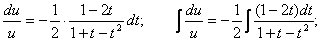
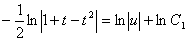
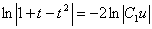
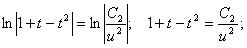
Енді алғашқы функция у және айнымалы х-ке ораламыз // :

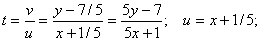
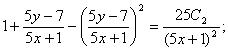
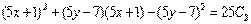
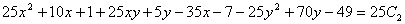
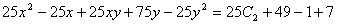
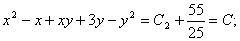
Сонымен, 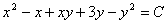өрнегі берілген теңдеудің жалпы интегралы болып табылады.

2) Егер алғашқы 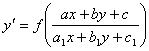теңдеуде анықтауыш 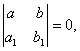онда 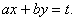алмастыруын жасаймыз.

Мысал: 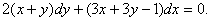теңдеуін шешу керек.

Шешуі: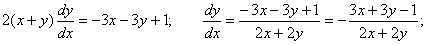

Анықтауышты есептейік: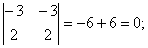

Ендеше 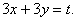алмастыруын жасаймыз.

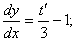
Бұл өрнекті алғашқы теңдеуге қоямыз:

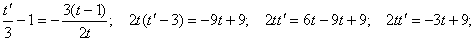
Айнамалыларды ажыратайық: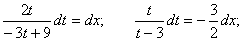

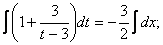
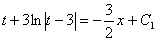
Енді алғашқы функция у және айнымалы х-ке ораламыз // :

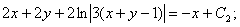
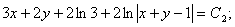
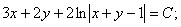
Сөйтіп, берілген теңдеудің жалпы интегралын таптық.

Аудиториялық жұмыстар

Теңдеудің түрін анықтап, жалпы шешімін (интегралын) жəне дара шешімін тап:

1) 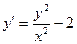жауабы: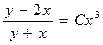

2) (y² − 3x² )dy + 2xydx = 0 ; у½_х=0=1 жауабы: y ² − x ² = y ³

3) y ² + x ² y ' = xy y ' жауабы: y = C₁ ⋅ e ^у/х

4) xdy-ydx=ydy , y(-1)=1 жауабы: x = − y(1 + lnïyï)

5) y ' = y/х + 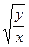жауабы: x= C₁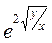

6) 2 x ² y ' = x ² + y ² ; у½_х=1=0 жауабы: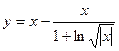

7) 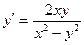жауабы: х²+у²=Су

8) xy ' − у = 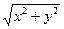, уï_х=0=1 жауабы: х²=0 жəне х²=4-4у

9) хy ' = уln 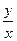жауабы:у=хе^1+Сх

10) (3у²+3ху+х²)dx=(x²+2xy)dy; у½_х=1=0 жауабы: (x+y)²=x³e^1-x/(x+y)

Й жұмыстары

Теңдеудің түрін анықтап, жалпы шешімін (интегралын) дара шешімін тап:

11) (x² + y² )dx − 2xydy = 0

12) у' = 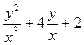, уï_х=1=0

13) y − xy ' = y ln x

14) 3у ' = 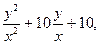уï_х=1=0

15) xydx − (x ² + y ²)dy = 0

16) (x + 7 y)dx − xdy = 0, уï_х=1=0

17) y ² + x ² y ' = xyy '

18) 8 xdy = (x + y)dx , уï_х=1=0

19) 2 x ³ y ' = y (2 x ² − y ² )

20) xy'= 3 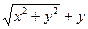, уï_х=1=1

21) xy '− y = xtg( y/х)