Поверхность второго порядка в трёхмерном пространстве
1°. Основные виды поверхностей второго порядка.
Пусть в трёхмерном пространстве задана, декартова прямоугольная система координат.
Рассмотрим уравнение
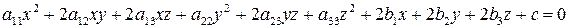 , , | (1) |
где среди коэффициентов 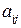 хотя бы один отличен от нуля. Множество точек пространства с координатами
хотя бы один отличен от нуля. Множество точек пространства с координатами 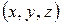 , удовлетворяющих уравнению (1), определяет, вообще говоря, некоторую поверхность, называемую поверхностью второго порядка. Если уравнение (1) не имеет ни одного решения, то будем говорить, что оно определяет мнимую поверхность.
, удовлетворяющих уравнению (1), определяет, вообще говоря, некоторую поверхность, называемую поверхностью второго порядка. Если уравнение (1) не имеет ни одного решения, то будем говорить, что оно определяет мнимую поверхность.
В некоторых случаях уравнение (1) может определять пару различных или совпадающих плоскостей или одну единственную точку. Но и такие множества будем называть поверхностями.
Перечислим важнейшие частные случай уравнения (1):
1) Эллипсоид
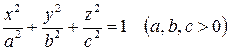 .
.
2) Однополостный гиперболоид
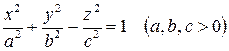 .
.
3) Двуполостный гиперболоид
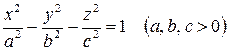 .
.
4) Эллиптический параболоид
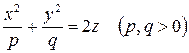 .
.
5) Гиперболический параболоид
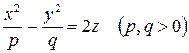 .
.
6) Конус второго порядка
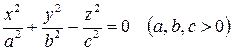 .
.
7) Точка
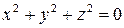 .
.
8) Цилиндры второго порядка:
цилиндр эллиптический
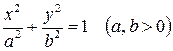 ,
,
цилиндр гиперболический
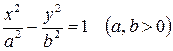 ,
,
цилиндр параболический
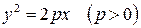 ,
,
пара пересекающихся плоскостей
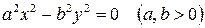 ,
,
пара параллельных или совпадающих плоскостей
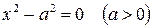 ,
,
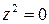 ,
,
прямая
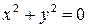 .
.
Остановимся теперь лишь на более подробном изучении уравнений и описываемых ими поверхностей, указанных выше восьми типов.
Эллипсоид
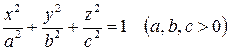 . . | (2) |
При 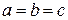 эллипсоид (2) обращается в сферу радиуса
эллипсоид (2) обращается в сферу радиуса 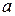 с центром в начале координат, т.е. геометрическое место точек, отстоящих от начала на расстоянии
с центром в начале координат, т.е. геометрическое место точек, отстоящих от начала на расстоянии 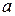 .
.
Величины 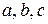 называются полуосями эллипсоида.
называются полуосями эллипсоида.
Если в уравнении (2) заменить (одновременно или порознь) 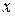 на
на 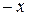 ,
, 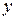 на
на  ,
, 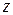 на
на 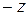 , то оно не изменится, – это показывает, что эллипсоид (2) есть поверхность, симметричная относительно координатных плоскостей
, то оно не изменится, – это показывает, что эллипсоид (2) есть поверхность, симметричная относительно координатных плоскостей 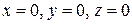 и начала координат. Поэтому достаточно изучить уравнение эллипсоида (2) в первом октанте (системы координат), т.е. для
и начала координат. Поэтому достаточно изучить уравнение эллипсоида (2) в первом октанте (системы координат), т.е. для 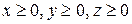 . Часть эллипсоида, находящаяся в первом октанте, определяется явным уравнением, например
. Часть эллипсоида, находящаяся в первом октанте, определяется явным уравнением, например
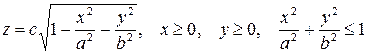 .
.
Для определённости будем считать, что 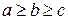 . Эллипсоид есть ограниченная поверхность. Он находится внутри шара радиуса
. Эллипсоид есть ограниченная поверхность. Он находится внутри шара радиуса 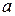 с центром в начале координат: для координат любой точки эллипсоида
с центром в начале координат: для координат любой точки эллипсоида 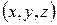 имеет место неравенство
имеет место неравенство
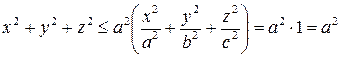 .
.
Чтобы составить более точное представление об эллипсоиде, произведём сечения плоскостями, параллельными координатным плоскостям. Например, пересекая эллипсоид плоскостями 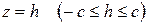 , получим в сечении эллипсы
, получим в сечении эллипсы
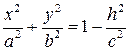
с полуосями
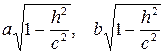 .
.
Отсюда видно, что самый большой эллипс получается в сечении эллипсоида плоскостью 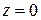 . Аналогичная картина будет при сечении плоскостями
. Аналогичная картина будет при сечении плоскостями 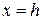
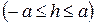 ,
, 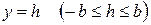 .
.
Эллипсоид (2) имеет вид, изображенный на рис. 1.
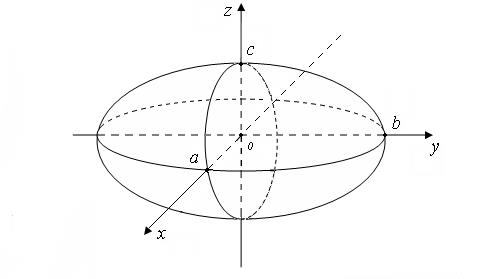
Рис. 1.
Точки 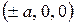 ,
, 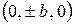 ,
, 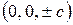 лежат на эллипсоиде (2) и называется его вершинами.
лежат на эллипсоиде (2) и называется его вершинами.
Если какие–либо две полуоси равны между собой, то эллипсоид (2) будет эллипсоидом вращения, т.е. получается от вращения эллипса относительно соответствующей оси координат.
Однополостный гиперболоид
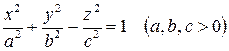 . . | (3) |
По виду уравнения (3) заключаем, что однополостный гиперболоид является поверхностью, симметричной относительно координатных плоскостей и начала координат. Числа 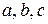 называются полуосями однополостного гиперболоида. Точка
называются полуосями однополостного гиперболоида. Точка 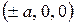 ,
, 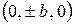 , лежащие на поверхности (3), называются вершинами однополостного гиперболоида.
, лежащие на поверхности (3), называются вершинами однополостного гиперболоида.
Пересечём поверхность (3) плоскостью 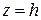 , тогда в сечении получим эллипс
, тогда в сечении получим эллипс
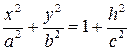
с полуосями
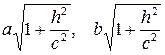 .
.
При изменении 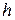 от
от 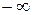 до
до 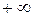 этот эллипс описывает поверхность (3).
этот эллипс описывает поверхность (3).
Если теперь пересечь поверхность (3) плоскостью 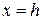 (или
(или 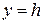 ), то получим в сечении гиперболу
), то получим в сечении гиперболу
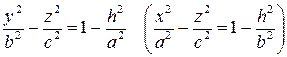 .
.
При 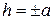 первая гипербола распадается на две прямые
первая гипербола распадается на две прямые 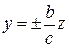 .
.
Если  , то действительной осью симметрии соответствующей гиперболы является прямая, параллельная оси
, то действительной осью симметрии соответствующей гиперболы является прямая, параллельная оси 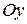 , а при
, а при 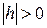 – прямая, параллельная оси
– прямая, параллельная оси 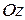 .
.
Действительной осью симметрии гиперболы мы называем ту из осей симметрии, которую гипербола пересекает.
Если 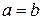 , то поверхность (3) в сечении плоскостями
, то поверхность (3) в сечении плоскостями 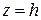 будет иметь окружности радиуса
будет иметь окружности радиуса 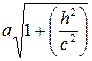 . Поверхность (3) в этом случае образуется от вращения гиперболы
. Поверхность (3) в этом случае образуется от вращения гиперболы 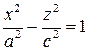 около оси
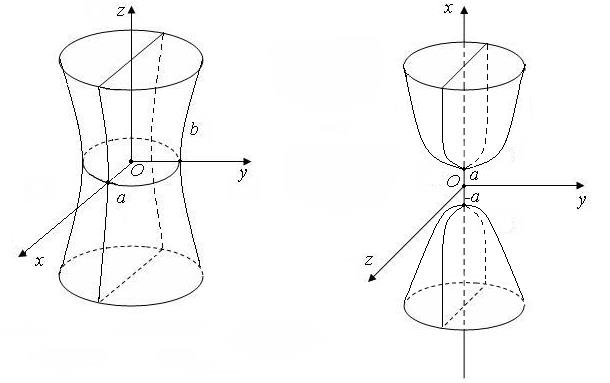
около оси 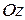 . Общий вид однополостного гиперболоида изображён на рис. 2.
. Общий вид однополостного гиперболоида изображён на рис. 2.
Двуполостный гиперболоид
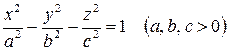 . . | (4) |
Так как уравнение (4) содержит только квадраты переменных, то данная поверхность симметрична относительно плоскостей 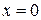 ,
, 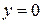 ,
, 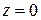 и начала координат.
и начала координат.
Уравнение (4) запишем ещё в виде
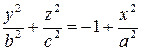 . . | ( 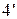 ) ) |
Отсюда ясно, что, пересекая поверхность ( 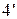 ) плоскостью
) плоскостью 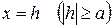 , получим в сечении эллипс
, получим в сечении эллипс
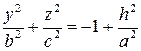
с полуосями
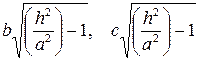 .
.
При 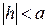 число
число 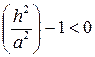 , и поэтому нет точек пересечения поверхности (
, и поэтому нет точек пересечения поверхности ( 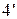 ) и плоскости
) и плоскости 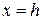 .
.
|
| Рис. 2. | Рис. 3. |
При сечении поверхности (4) плоскостями 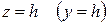 получим гиперболы
получим гиперболы
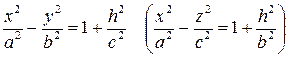 .
.
Точки 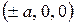 лежат на поверхности (4) и называются вершинами двуполостного гиперболоида. Поверхность (4) изображена на рис. 3.
лежат на поверхности (4) и называются вершинами двуполостного гиперболоида. Поверхность (4) изображена на рис. 3.
Эллиптический параболоид
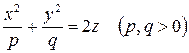 . . | (5) |
Так как (5) присутствуют квадраты переменных 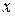 и
и 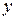 , то данная поверхность симметрична относительно координатных плоскостей
, то данная поверхность симметрична относительно координатных плоскостей 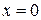 ,
, 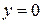 . Далее, так как мы считаем
. Далее, так как мы считаем 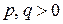 , то поверхность (5) расположена в полупространстве
, то поверхность (5) расположена в полупространстве 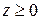 .
.
Пересекая поверхность (5) плоскостями 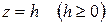 , в сечении будем получать эллипсы
, в сечении будем получать эллипсы
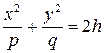
с полуосями
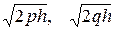 .
.
При изменении 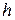 от нуля до
от нуля до 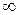 данные эллипса описывают нашу поверхность (5).
данные эллипса описывают нашу поверхность (5).
Пересекая поверхность (5) плоскостями 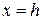 (или
(или 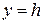 ), мы получим в сечении параболы
), мы получим в сечении параболы
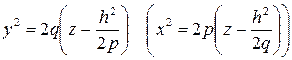
со смещённой вершиной в точке 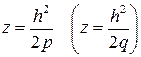 .
.
При 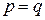 поверхность (5) будет поверхностью вращения, получающейся от вращения параболы
поверхность (5) будет поверхностью вращения, получающейся от вращения параболы 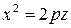 около оси
около оси 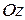 . В этом случае поверхность (5) называют параболоидом вращения.
. В этом случае поверхность (5) называют параболоидом вращения.
Точка 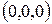 лежит на поверхности (5) и называется вершиной эллиптического параболоида. Эллиптический параболоид изображён на рис. 4.
лежит на поверхности (5) и называется вершиной эллиптического параболоида. Эллиптический параболоид изображён на рис. 4.
Гиперболический параболоид
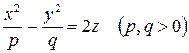 . . | (6) |
По виду уравнения (6) заключаем, что данная поверхность симметрична относительно плоскостей 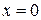 ,
, 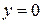 . Пересекая поверхность (6) плоскостями
. Пересекая поверхность (6) плоскостями 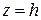 , мы будем получать в сечении гиперболы
, мы будем получать в сечении гиперболы
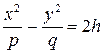 ,
,
причём при  действительная ось симметрии гиперболы будет параллельной оси
действительная ось симметрии гиперболы будет параллельной оси 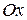 , а при
, а при 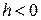 – оси
– оси 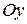 . При
. При 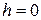 в сечении будут две пересекающиеся прямые.
в сечении будут две пересекающиеся прямые.
При сечении поверхности (6) плоскостями 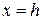 или
или 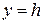 , получим параболы, направленные ветвями вниз или вверх:
, получим параболы, направленные ветвями вниз или вверх:
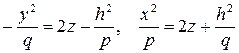 .
.
Поверхность (6) изображена на рис. 5.
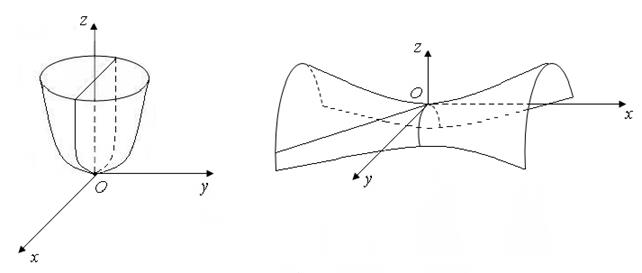
| Рис. 4. | Рис. 5. |
Конус второго порядка
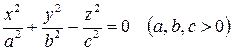 . . | (7) |
Данная поверхность симметрична относительно плоскостей 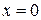 ,
, 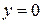 ,
, 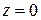 и начала координат.
и начала координат.
При сечении поверхности (7) плоскостями 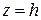 будем получать эллипсы
будем получать эллипсы
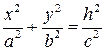
с полуосями 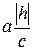 и
и 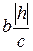 .
.
Если же пересекать поверхность (7) плоскостями 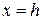 или
или 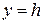 , то в сечении получим гиперболы
, то в сечении получим гиперболы
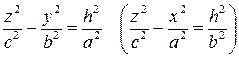 .
.
Если теперь пересекать (7) плоскостями 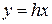 , то в сечении получим пару пересекающихся прямых
, то в сечении получим пару пересекающихся прямых
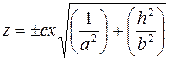 .
.
Вид конуса изображён на рис. 6.
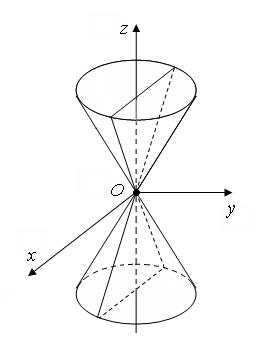
Рис. 6.
Точка
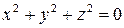 . . | (8) |
Уравнению (8) удовлетворяет только одна точка 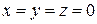 .
.
Цилиндры второго порядка
а) Эллиптический цилиндр
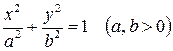 . . | (9) |
Уравнение (9) не содержит переменной 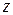 . На плоскости
. На плоскости 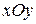 уравнение (9) определяет эллипс с полуосями
уравнение (9) определяет эллипс с полуосями 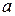 и
и 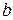 . Если точка
. Если точка 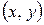 лежит на этом эллипсе, то при любом
лежит на этом эллипсе, то при любом 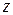 точка
точка 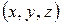 лежит на поверхности (9). Совокупность таких точек есть поверхность, описанная прямой, параллельной оси
лежит на поверхности (9). Совокупность таких точек есть поверхность, описанная прямой, параллельной оси 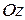 и пересекающей эллипс
и пересекающей эллипс
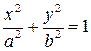
в плоскости 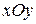 .
.
Эллипс (9) называют направляющей линией данной поверхности, а все возможные положения движущейся прямой – образующими.
Вообще поверхность, описываемая прямой, остающейся параллельной некоторому заданному направлению и пересекающей данную линию 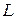 , называется цилиндрической. Поверхность (9) изображена на рис. 7.
, называется цилиндрической. Поверхность (9) изображена на рис. 7.
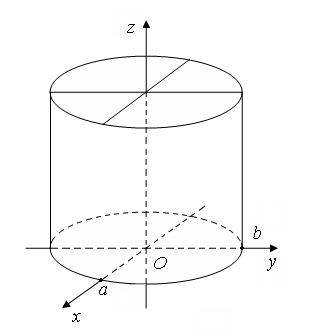
Рис. 7.
б) Гиперболический и параболический цилиндры
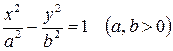 , , | (10) |
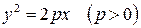 . . | (11) |
В данном случае направляющими линиями поверхностей являются гипербола и парабола, а образующими – прямые, параллельные оси 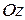 и проходящие через гиперболу и параболу в плоскости
и проходящие через гиперболу и параболу в плоскости 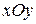 . Поверхности (10) и (11) изображены на рис. 8 и 9.
. Поверхности (10) и (11) изображены на рис. 8 и 9.
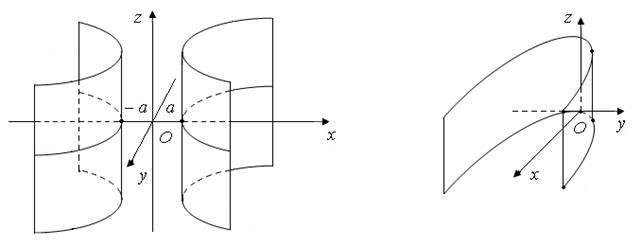
| Рис. 8. | Рис. 9. |
в) Параллельные и пересекающиеся плоскости. Прямая
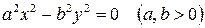 , , | (12) |
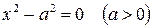 , , | (13) |
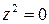 , , | (14) |
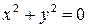 | (15) |
Для поверхности (12) направляющими являются прямые линии
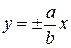 .
.
Поэтому поверхность (12) есть пара пересекающихся плоскостей. В уравнении поверхностей (13) и (14) отсутствуют по две координаты. Уравнение (13) в плоскости 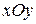 есть пара прямых
есть пара прямых 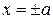 .
.
Если мы будем брать 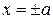 и любые
и любые 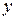 и
и 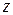 , то точки
, то точки 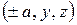 будут удовлетворять уравнению (13), поэтому поверхность (13) есть пара параллельных плоскостей.
будут удовлетворять уравнению (13), поэтому поверхность (13) есть пара параллельных плоскостей.
Уравнение (14) описывает плоскость 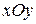 , так как этому уравнению удовлетворяют любые точки вида
, так как этому уравнению удовлетворяют любые точки вида 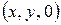 , всё множество которых и составляет плоскость
, всё множество которых и составляет плоскость 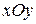 .
.
Можно также рассматривать 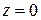 как направляющую в какой–либо из плоскостей
как направляющую в какой–либо из плоскостей 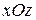 или
или 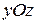 , а образующими являются прямые, параллельные оси
, а образующими являются прямые, параллельные оси 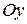 или оси
или оси 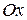 и проходящие через прямую
и проходящие через прямую 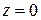 .
.
Уравнению (15) удовлетворяет любая точка с 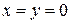 и любым
и любым 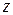 . Поэтому (15) изображает прямую, а именно, ось
. Поэтому (15) изображает прямую, а именно, ось 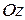 .
.
Линейчатые поверхности
Некоторые второго порядка образованы движением прямой. Такими являются все цилиндрические поверхности и конус второго порядка. Однако имеются и другие поверхности, которые также образуются движением прямой.
Поверхность, образованная движением прямой, называется линейчатой, а целиком лежащие на ней прямые – прямолинейными образующими.
К линейчатым поверхностям относятся однополостный гиперболоид и гиперболический параболоид.
Уравнение однополостного гиперболоида (3) можно записать в виде
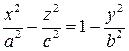
или, разлагая левую и правую части на множители, получаем
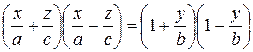 . . | (16) |
Составим систему уравнений первой степени:
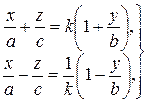 | (17) |
где 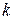 – произвольный параметр.
– произвольный параметр.
При определённом значении этого параметра 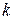 мы получим прямую линию, а при изменении
мы получим прямую линию, а при изменении 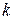 – семейство прямых. Если мы перемножим уравнения (17) почленно, то получим уравнение (16) нашей поверхности. Поэтому любая точка
– семейство прямых. Если мы перемножим уравнения (17) почленно, то получим уравнение (16) нашей поверхности. Поэтому любая точка 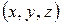 , удовлетворяющая системе (17), находится на поверхности (16). Следовательно, каждая из прямых семейства (17) целиком лежит на поверхности однополостного гиперболоида.
, удовлетворяющая системе (17), находится на поверхности (16). Следовательно, каждая из прямых семейства (17) целиком лежит на поверхности однополостного гиперболоида.
Совершенно аналогично система
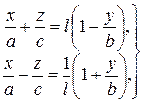 | (18) |
где 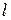 – параметр, также определяет семейство прямых, отличное от семейства (17), принадлежащее поверхности (16).
– параметр, также определяет семейство прямых, отличное от семейства (17), принадлежащее поверхности (16).
Через каждую точку гиперболоида (16) проходит по одной прямой каждого семейства, вообще при различных значениях параметров 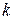 и
и 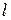 (рис. 10).
(рис. 10).
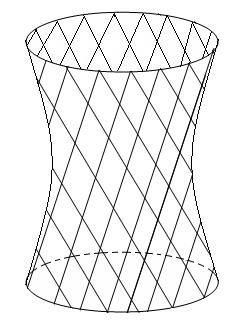
Рис. 10.
2°. Исследование общего уравнения второго порядка с тремя переменными.
Пусть поверхность второго порядка задана уравнением (1):
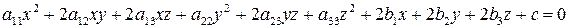 .
.
Также как и в случае линий второго порядка, путём преобразований поворота и переноса координатной системы уравнения (1) сложно привести к некоторому каноническому виду. Оказывается, существует ровно 17 типов канонических уравнений второго порядка, которые и будут получены ниже.
Вначале рассмотрим квадратичную форму
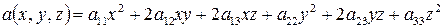 ,
,
фигурирующую в левой части уравнения (1). На основании теоремы 1 из §13 существует ортогональное преобразование базисных векторов (представляющее собой преобразование поворота) такое, что в левом базисе квадратичная форма имеет диагональный вид:
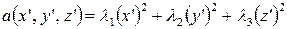 .
.
Тогда в новой прямоугольной системе координат исследуемая поверхность имеет уравнение
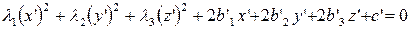 | (19) |
(более подробно переход от уравнения (1) к уравнению (19) будет обсуждаться при исследовании общего уравнение квадрики, см. §18).
А. Пусть все три числа 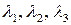 отличны от нуля. Тогда по аналогии с предложением 1 из §14 можно построить преобразования переноса такие, что уравнение (19) примет вид
отличны от нуля. Тогда по аналогии с предложением 1 из §14 можно построить преобразования переноса такие, что уравнение (19) примет вид
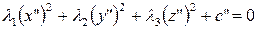 . . | (20) |
А.1. Пусть 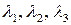 одинакового знака. Имеются три возможности.
одинакового знака. Имеются три возможности.
А.1а. Если знак 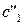 противоположен знаку
противоположен знаку 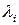 , то уравнение (20) можно переписать в виде
, то уравнение (20) можно переписать в виде
| (1) | 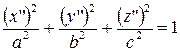 . . |
Т.е. полученная поверхность является эллипсоидом.
А.1б. Если знак 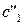 совпадает со знаком
совпадает со знаком 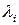 , то (20) принимает вид
, то (20) принимает вид
| (2) | 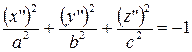 – – |
– мнимый эллипсоид.
А.1в. Если 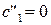 , то (20) принимает вид
, то (20) принимает вид
| (3) | 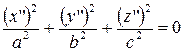 . . |
Этому уравнению удовлетворяет единственная точка, а именно нулевая точка 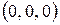 .
.
А.2. Пусть два из чисел 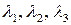 имеют один знак, а третье – противоположный им знак.
имеют один знак, а третье – противоположный им знак.
А.2а. Если  , то умножая на
, то умножая на 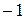 и переставляя, если нужно, переменные, уравнение (20) можно привести к одному из следующих видов
и переставляя, если нужно, переменные, уравнение (20) можно привести к одному из следующих видов
| (4) | 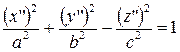 – – |
– однополостный гиперболоид,
| (5) | 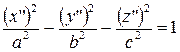 – – |
– двуполостный гиперболоид.
А.2б. Если 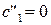 , то (20) принимает вид:
, то (20) принимает вид:
| (6) | 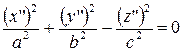 – – |
– уравнение конуса.
Б. Пусть одно 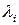 равно нулю. Будем считать, что
равно нулю. Будем считать, что 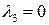 . Тогда переносом по
. Тогда переносом по 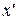 и
и 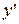 уравнение (19) приводится к виду
уравнение (19) приводится к виду
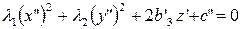 . . | (21) |
Б.1. Если 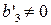 , то после переноса по
, то после переноса по 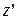 из (21) получаем
из (21) получаем
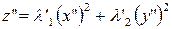 .
.
Б.1а. Если 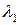 и
и 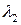 имеют одинаковый знак то (заменяя при необходимости
имеют одинаковый знак то (заменяя при необходимости 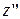 на
на 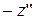 ) получаем
) получаем
| (7) | 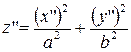 – – |
– эллиптический параболоид.
Б.1б. Если 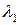 и
и 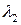 – разных знаков, то получаем
– разных знаков, то получаем
| (8) | 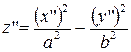 – – |
– гиперболический параболоид.
Б.2. Если в (21) 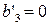 , то (21) является цилиндрической поверхностью и возможны следующие случаи.
, то (21) является цилиндрической поверхностью и возможны следующие случаи.
Б.2а. 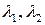 имеют одинаковый знак, противоположный знаку
имеют одинаковый знак, противоположный знаку 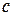 :
:
| (9) | 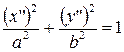 – – |
– эллиптический цилиндр.
Б.2б. 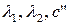 , имеют одинаковый знак:
, имеют одинаковый знак:
| (10) | 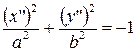 – – |
– мнимый эллиптический цилиндр.
Б.2в. 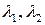 имеют одинаковый знак,
имеют одинаковый знак, 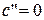 :
:
| (11) | 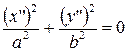 – – |
– пара мнимых пересекающихся плоскостей.
Б.2г. 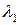 и
и 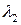 имеют различные знаки,
имеют различные знаки, 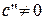 :
:
| (12) | 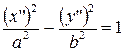 – – |
– гиперболический цилиндр.
Б.2д. 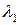 и
и 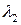 имеют различные знаки,
имеют различные знаки, 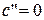 :
:
| (13) | 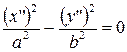 – – |
– две пересекающиеся плоскости.
В. Пусть 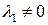 ,
,  . Тогда уравнение (19) после переноса по
. Тогда уравнение (19) после переноса по 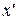 принимает вид:
принимает вид:
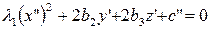 . . | (22) |
В.1. Пусть хотя бы одно из 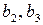 не равно нулю. Выполним поворот координатной системы
не равно нулю. Выполним поворот координатной системы 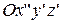 вокруг оси
вокруг оси 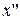 на угол
на угол 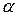 такой, что
такой, что
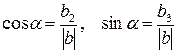 ,
,
где 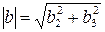 .
.
Тогда новые координаты 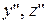 связаны со старыми
связаны со старыми 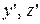 формулами
формулами
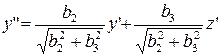 ,
,
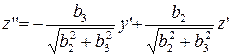
и уравнение (22) в новой системе координат принимает вид
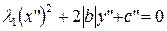 .
.
Далее после переноса вдаль  получаем уравнение вида
получаем уравнение вида
| (14) | 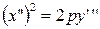 – – |
– параболический цилиндр.
В.2. Если 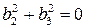 , то уравнение (22) имеет вид
, то уравнение (22) имеет вид
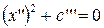
и возможны следующие три случая.
В.2а. 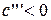 :
:
| (15) | 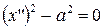 – – |
– пара параллельных плоскостей.
В.2б. 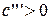 :
:
| (16) | 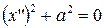 – – |
– пара мнимых параллельных плоскостей.
В.2в. 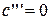 :
:
| (17) | 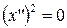 – – |
– пара совпадающих плоскостей.
