Прямая линия в трёхмерном пространстве
Способы задания прямой
I. Пусть d – какая-либо прямая в пространстве, точка 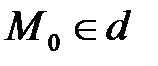 ,
, 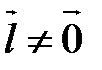 и
и 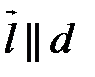 .
.
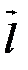 – направляющий вектор прямой.
– направляющий вектор прямой.
Тогда произвольная точка 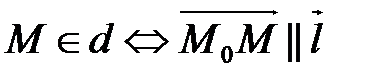 . По теореме о коллинеарных векторах верно равенство
. По теореме о коллинеарных векторах верно равенство 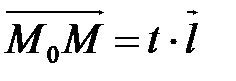 ,
, 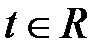 , (1)
, (1)
это векторно-параметрическое уравнение прямой.
Таким образом, чтобы задать прямую d, достаточно задать одну ее точку 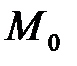 и направляющий вектор
и направляющий вектор 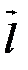 . Обозначение:
. Обозначение: 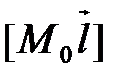 .
.
Уравнение (1) устанавливает взаимно-однозначное соответствие между точками прямой d и значениями параметра 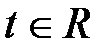 . Параметр t является координатой точки M в системе координат
. Параметр t является координатой точки M в системе координат 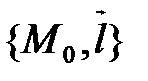 на прямой d.
на прямой d.
Введем аффинную систему координат 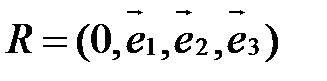 в пространстве. Тогда
в пространстве. Тогда 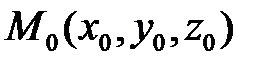 ,
, 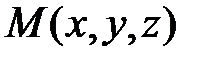 ,
, 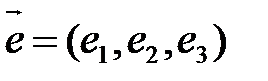 .
.
Из (1), переходя к координатам, имеем: 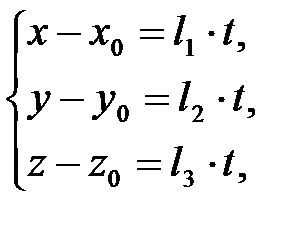 или
или 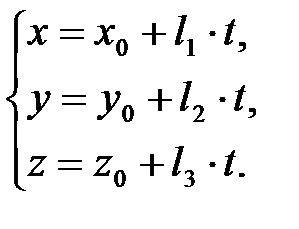 (2)
(2)
Обратно, из (2) следует (1). Значит, (2) определяет прямую d в пространстве. Уравнения (2) называются параметрическими уравнениями прямой.
II. Пусть в уравнениях (2) 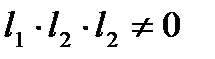 . Из (2) выразим t:
. Из (2) выразим t:
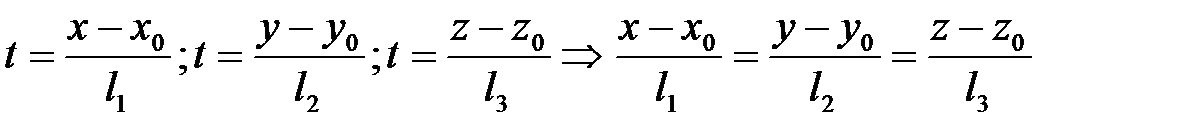 . (3)
. (3)
а) Пусть одна какая-либо координата вектора 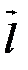 равна нулю, например,
равна нулю, например, 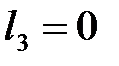 .
.
Тогда из (2) следует система уравнений: 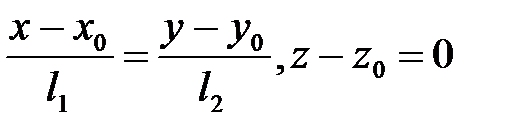 . (3')
. (3')
Здесь, т.к. 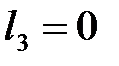 , то
, то 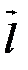 || (XOY), а, значит, и d || (XOY).
|| (XOY), а, значит, и d || (XOY).
б) Пусть две координаты направляющего вектора 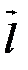 равны нулю, например,
равны нулю, например, 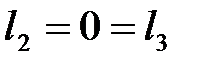 .
.
Из (2) следует система: 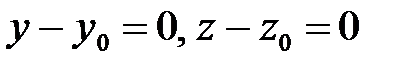 . (3'')
. (3'')
Тогда 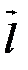 || (OX), а, значит, и d || (OX).
|| (OX), а, значит, и d || (OX).
Уравнения (3), (3'), (3'') называются каноническими уравнениями прямой.
III. Прямая d однозначно определена, если заданы две ее точки, например, 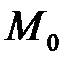 ,
, 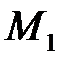 . Тогда за направляющий вектор
. Тогда за направляющий вектор 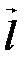 можно принять вектор
можно принять вектор 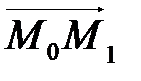 . Пусть в репере
. Пусть в репере 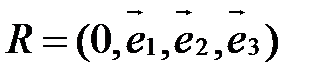 введены координаты
введены координаты 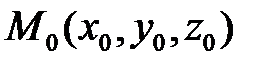 ,
, 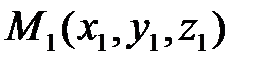 , значит,
, значит, 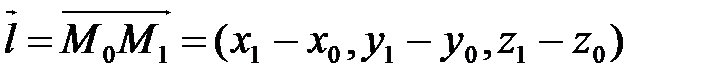 .
.
Из системы (2) получим 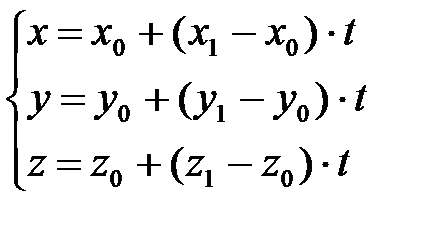 , или, выделяя из каждого уравнения t и приравнивая, имеем:
, или, выделяя из каждого уравнения t и приравнивая, имеем: 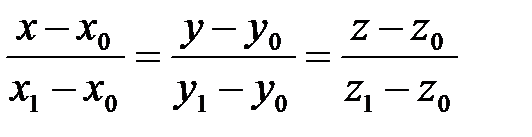 . (4)
. (4)
IV. Прямая может быть задана как пересечение двух плоскостей 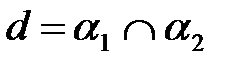 .
.
Пусть в репере 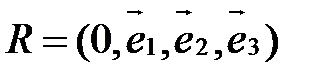 плоскости заданы уравнениями
плоскости заданы уравнениями
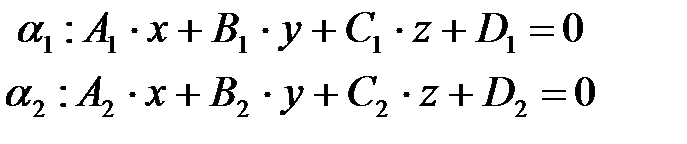 (5)
(5)
И ранг матрицы 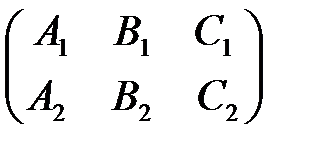 равен 2 (т.к.
равен 2 (т.к. 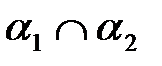 ).
).
Тогда система уравнений (5) определяет прямую d.
Замечание: Рассмотрим векторы нормалей к плоскостям 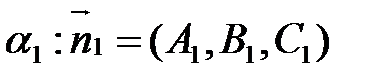 и
и 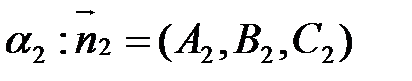 . Тогда вектор
. Тогда вектор 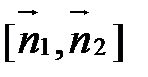 будет параллелен d. Т.е. можно считать направляющим вектором прямой d вектор
будет параллелен d. Т.е. можно считать направляющим вектором прямой d вектор 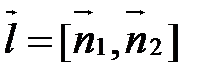 . Координаты его можно определить
. Координаты его можно определить 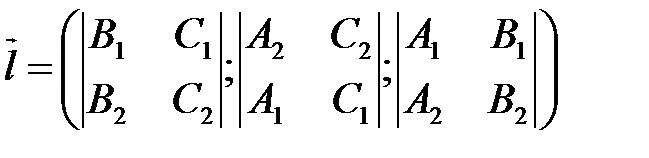 .
.
Взаимное расположение прямой и плоскости
Пусть в репере 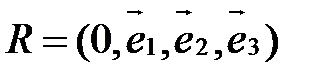 прямая d задана параметрически
прямая d задана параметрически
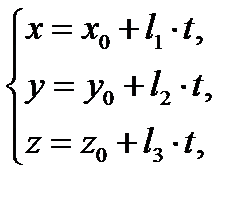
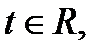 (1)
(1)
а плоскость α задана общим уравнением: 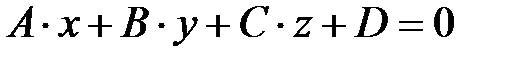 . (2)
. (2)
Будем искать общие точки прямой и плоскости, т.е. решения системы уравнений (1) и (2). Подставим (1) в (2) и сгруппируем по t:
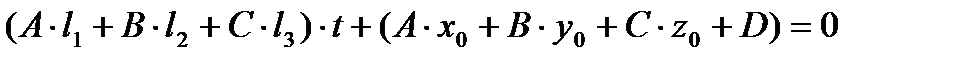 . (3)
. (3)
Могут быть следующие случаи:
1. Система уравнений (1), (2) имеет единственное решение тогда и только тогда, когда (3) имеет единственное решение: 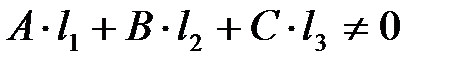 . (4)
. (4)
Т.е. условие (4) является необходимым и достаточным условием пересечения прямой d и плоскости α.
В 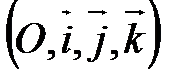 выражение (4) имеет следующий геометрический смысл:
выражение (4) имеет следующий геометрический смысл:
1) если 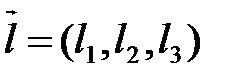 – направляющий вектор прямой d и
– направляющий вектор прямой d и 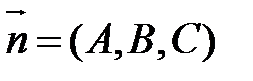 – вектор нормали плоскости α, то
– вектор нормали плоскости α, то 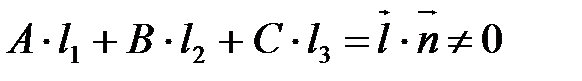 по (4), а, значит,
по (4), а, значит, 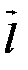 и
и 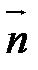 не перпендикулярны;
не перпендикулярны;
2) прямая d ^ α 
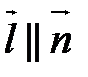 , т.е. когда ранг матрицы
, т.е. когда ранг матрицы 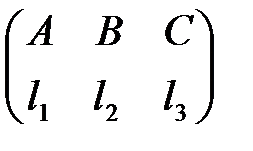 равен 1.
равен 1.
2. Система из (1) и (2) не имеет решений тогда и только тогда, когда (3) не имеет решений, т.е. когда
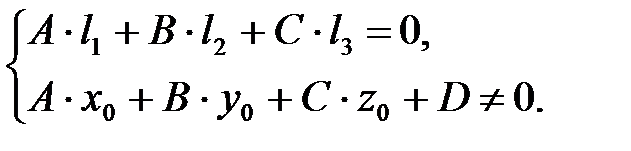 (5)
(5)
Условия (5) являются критерием того, что d и α не имеют общих точек.
В прямоугольной системе координат они означают, что 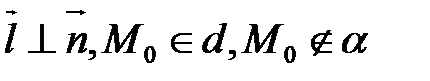 .
.
3. Система уравнений (1) и (2) имеет бесконечное множество решений тогда и только тогда, когда уравнение (3) удовлетворяет любым значениям t, т.е. когда
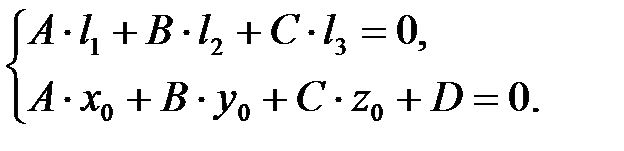 (6)
(6)
Значит, условия (6) являются критерием того, что 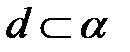 .
.
В прямоугольной системе координат система (6) означает, что 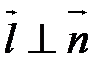 ,
, 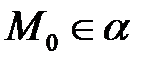 и
и 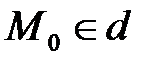 .
.
Из (5) и (6) заключаем, что 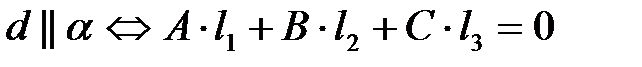 .
.
Взаимное расположение двух прямых в трёхмерном пространстве
Пусть имеются две прямые 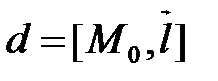 и
и 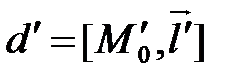 , каждая из которых задана точкой и направляющим вектором с координатами в аффинной системе координат
, каждая из которых задана точкой и направляющим вектором с координатами в аффинной системе координат 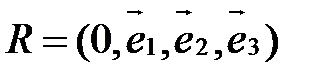 :
: 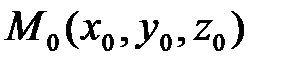 ,
, 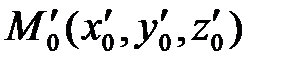 ,
, 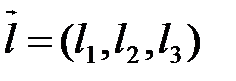 ,
, 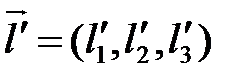 .
.
1. Прямые d и d¢ лежат в одной плоскости 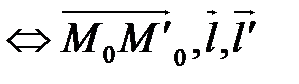 – компланарны., то есть в координатной форме:
– компланарны., то есть в координатной форме:
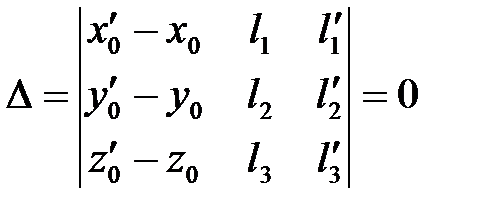 или смешанное произведение
или смешанное произведение 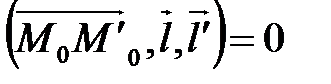 .
.
Пусть d и d¢ лежат в одной плоскости, тогда они пересекаются или параллельны.
а) 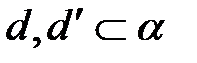 и
и 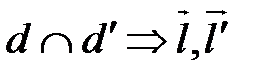 – неколлинеарны
– неколлинеарны 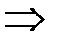 ранг матрицы
ранг матрицы 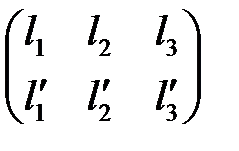 равен
равен 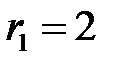 .
.
б) 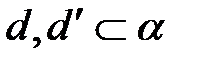 и
и 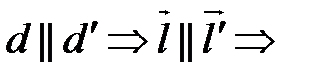
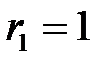 .
.
Параллельность прямых распадается на два случая:
*) Если 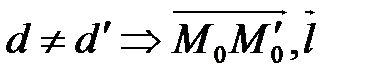 неколлинеарны, то отсюда следует, что
неколлинеарны, то отсюда следует, что 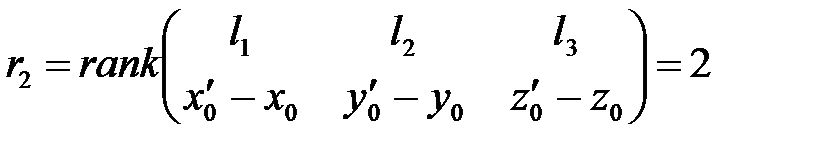 .
.
**) Если 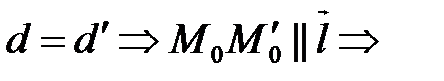
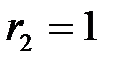 .
.
Методом от противного можно доказать достаточность этих условий.
2. Прямые d и d¢ не лежат в одной плоскости, значит, они скрещиваются. Тогда 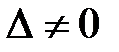 или
или 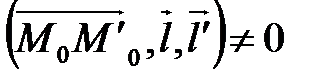 .
.
Угол между прямой и плоскостью
Определение. Углом между прямой d и не перпендикулярной к ней плоскостью α называется острый угол между этой прямой и ее ортогональной проекцией d´ на плоскость α.
Пусть в 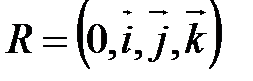 :
: 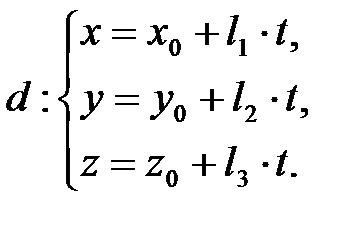 (1)
(1)
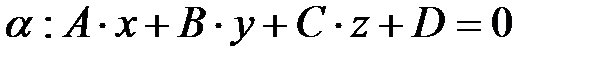 , (2)
, (2)
где d и α не перпендикулярны.
Обозначим 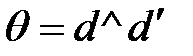 , где
, где 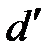 – ортогональная проекция d на α;
– ортогональная проекция d на α; 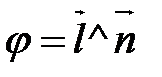 , где
, где 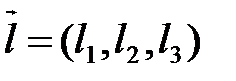 ,
, 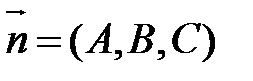 .
.
Если φ – острый угол, то 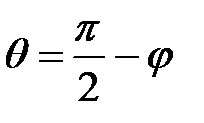 и
и 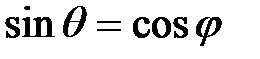 .
.
Если φ – тупой угол, то 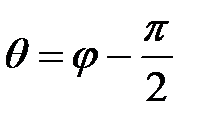 и
и 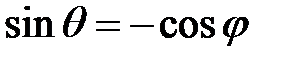 .
.
Тогда 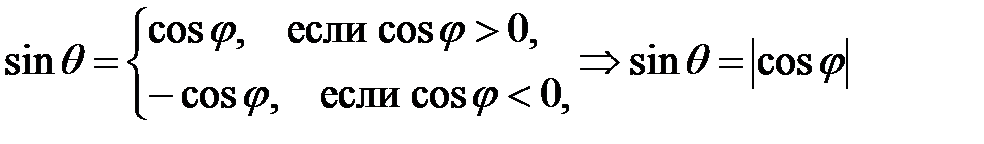 .
.
Значит, 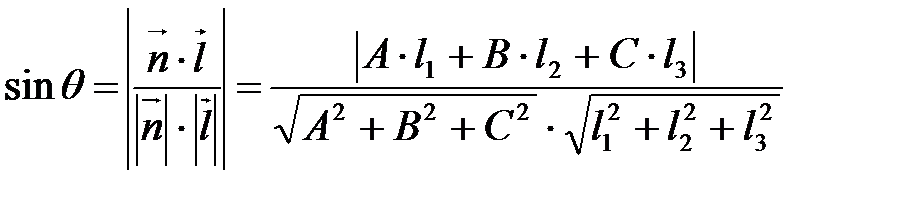 .
.
Угол между двумя прямыми в пространстве
Пусть в 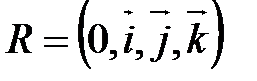 прямые
прямые 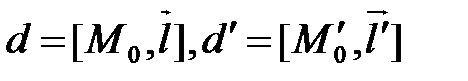 заданы каждая точкой и направляющим вектором:
заданы каждая точкой и направляющим вектором: 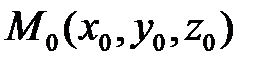 ,
, 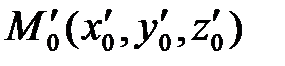 ,
, 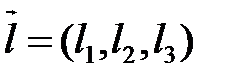 ,
, 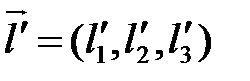 .
.
Определение. Угол между прямыми d и d´ в пространстве определяется как угол между прямыми, параллельными данным и проходящими через одну точку.
Его величина может быть найдена как величина угла между направляющими векторами данных прямых по формуле:
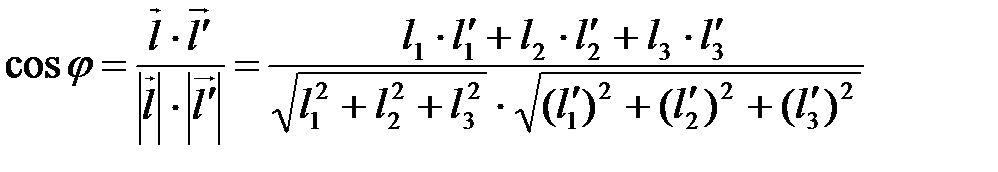 .
.
Следствие: 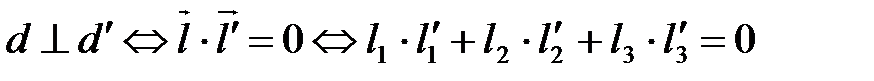 .
.
Расстояние от точки до прямой в пространстве
Пусть в 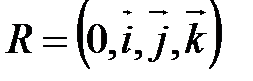 прямая
прямая 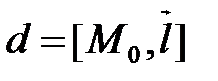 задана точкой и направляющим вектором:
задана точкой и направляющим вектором: 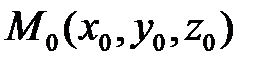 ,
, 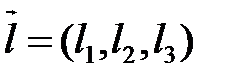 и дана точка
и дана точка 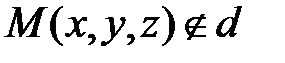 .
.
Построим 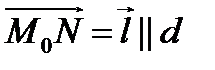 , достроим параллелограмм MM0NK, тогда
, достроим параллелограмм MM0NK, тогда 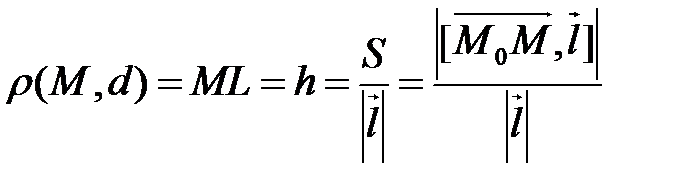 , где h – высота параллелограмма, S – площадь параллелограмма.
, где h – высота параллелограмма, S – площадь параллелограмма.
Уравнение общего перпендикуляра двух скрещивающихся прямых
Пусть в 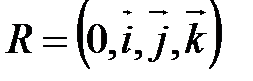 прямые
прямые 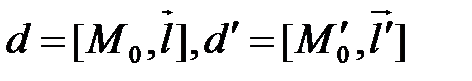 заданы каждая точкой и направляющим вектором:
заданы каждая точкой и направляющим вектором: 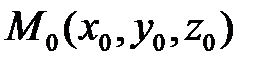 ,
, 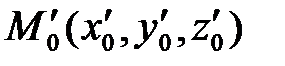 ,
, 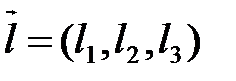 ,
, 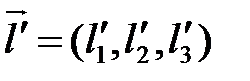 .
.
Тогда из критерия компланарности векторов 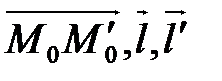 следует, что
следует, что
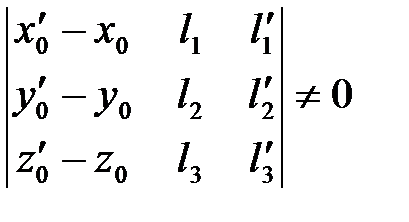 .
.
Необходимо найти уравнение прямой m такой, что 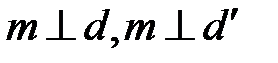 . Тогда
. Тогда 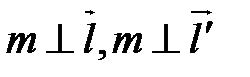 , тогда можно рассмотреть
, тогда можно рассмотреть 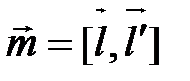 , и пусть
, и пусть 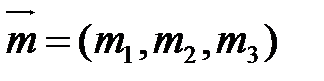 .
.
Прямую m будем искать как пересечение плоскостей α и β:
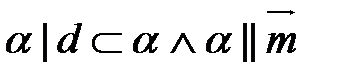 ,
,
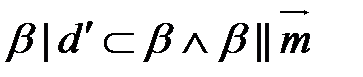 .
.
Рассмотрим плоскость α: 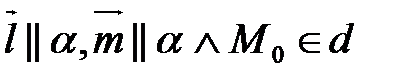 (а значит
(а значит 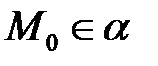 )
) 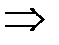
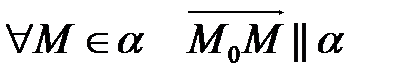 . Следовательно, векторы
. Следовательно, векторы 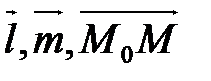 – компланарны, то есть
– компланарны, то есть
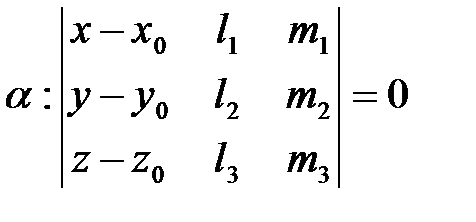 .
.
Аналогично 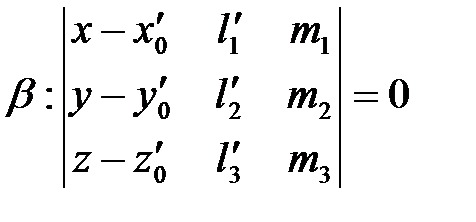 .
.
Тогда искомый перпендикуляр – прямая m, задается системой уравнений плоскостей α и β.
Кратчайшее расстояние между скрещивающимися прямыми
Кратчайшее расстояние между скрещивающимися прямыми – это длина отрезка общего перпендикуляра, заключенного между данными прямыми.
Пусть в 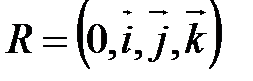 прямые
прямые 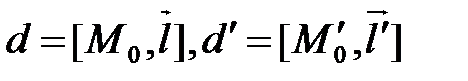 заданы каждая точкой и направляющим вектором:
заданы каждая точкой и направляющим вектором: 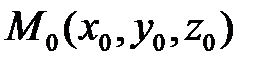 ,
, 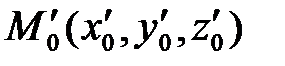 ,
, 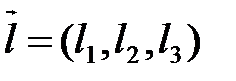 ,
, 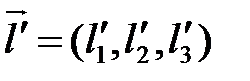 .
.
Тогда 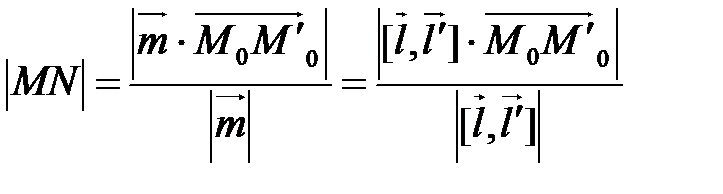 . Здесь
. Здесь 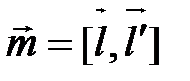 – направляющий вектор общего перпендикуляра двух данных прямых.
– направляющий вектор общего перпендикуляра двух данных прямых.
