Ряд а) расходится, ряд в) сходится 2 страница

5. Уравнение касательной к графику функции 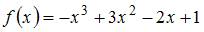в его точке с абсциссой 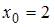имеет вид …

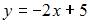- правильно

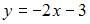
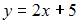
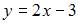
Решение:
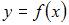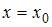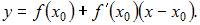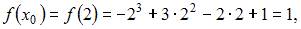
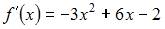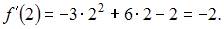Уравнение касательной к графику функции в его точке с абсциссой имеет вид Вычислим последовательно и Тогда уравнение касательной примет вид 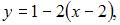или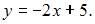

6. График функции 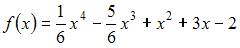будет выпуклым вверх при …

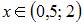- правильно

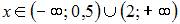
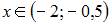
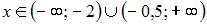
Решение:
График данной функции будет выпуклым вниз при условии, что 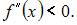Вычислим последовательно
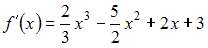и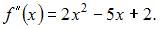
Тогда 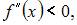при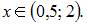

7. Наибольшее значение функции 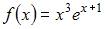на отрезке 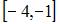равно …

– 1

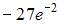
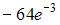
Тема 8: Дифференциалы и теоремы о дифференцируемых функциях
1. Дифференциал второго порядка функции 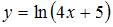равен …

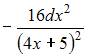- правильно

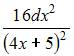
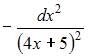
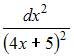
2. Приближенное значение функци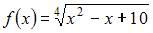и при 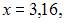вычисленное с использованием дифференциала первого порядка, равно …

2,025

1,975

2,01

2,1

Решение:
Воспользуемся приближенной формулой:

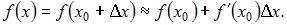
Полагая 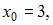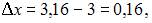приходим к равенству

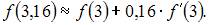
Вычислив последовательно

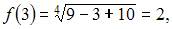
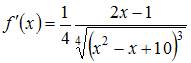и 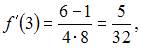получаем

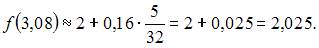
3. Дана функция 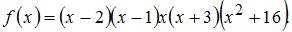Тогда меньший действительный корень производной этой функции принадлежит промежутку …

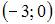- правильно

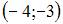
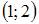
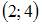
Решение:
Эта функция представляет собой полином 6-го порядка и дифференцируема на всей числовой оси. Согласно теореме Роля, между двумя корнями (нулями) этой функции находится по крайней мере один корень ее производной. Поскольку 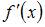представляет собой полином (6-го порядка), то между двумя корнями функции 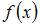находится ровно один корень ее производной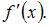
Найдем корни функции 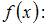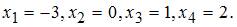Тогда меньший действительный корень функции 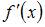принадлежит интервалу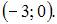

4. Приближенное значение функци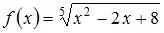и при 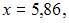вычисленное с использованием дифференциала первого порядка, равно …

1,9825

2,0125

1,375

1,875

Решение:
Воспользуемся приближенной формулой:

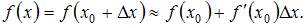
Полагая 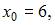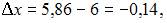приходим к равенству

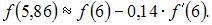
Вычислив последовательно

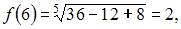
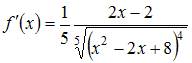и 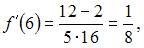получаем

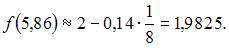
5. Дана функция 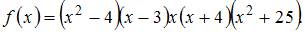Тогда больший действительный корень производной этой функции принадлежит промежутку …

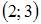- правильно

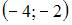
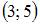
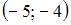
Решение:
Эта функция представляет собой полином седьмого порядка и дифференцируема на всей числовой оси. Согласно теореме Роля, между двумя корнями (нулями) этой функции находится по крайней мере один корень ее производной. Поскольку 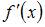представляет собой полином (7-го порядка), то между двумя корнями функции 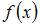находится ровно один корень ее производной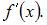
Найдем корни функции 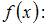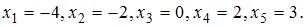Тогда больший действительный корень функции 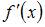принадлежит интервалу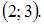

6. Для вычисления предела 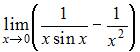один раз применили правило Лопиталя. Тогда предел примет вид …

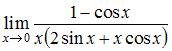- правильно

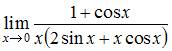
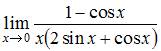
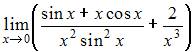
Решение:

Так как 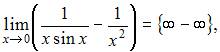то при помощи алгебраических преобразований получим неопределенность вида 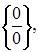или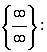

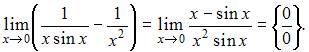
Тогда можно воспользоваться формулой вида 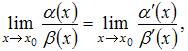что приводит к пределу:

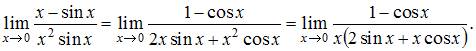
7. Дифференциал функции 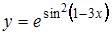равен …

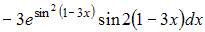- правильно

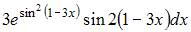
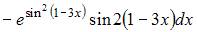
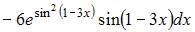
Решение:
Дифференциал 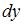функции 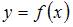выражается формулой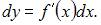
Тогда вычислив

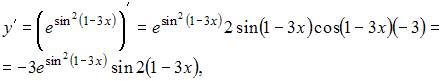
получаем, что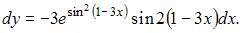

Тема 9: Частные производные первого порядка
1. Частная производная 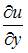функции 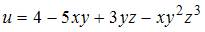имеет вид …

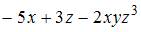- правильно

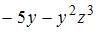
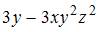
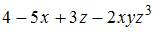
Решение:
При вычислении частной производной 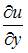по переменной 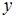переменные 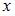и 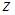рассматриваем как постоянные величины. Тогда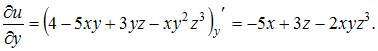

2. Частная производная 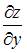функции 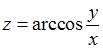имеет вид …

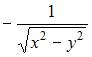- правильно

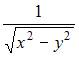
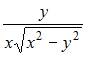
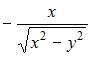
Решение:
При вычислении частной производной 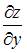по переменной 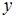переменную 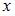рассматриваем как постоянную величину. Тогда

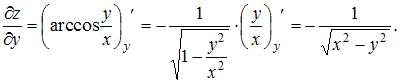
3. Частная производная 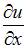функции 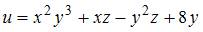имеет вид …

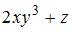- правильно

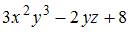
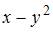
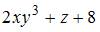
Решение:

При вычислении частной производной 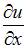по переменной 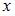переменные 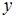и 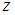рассматриваем как постоянные величины. Тогда

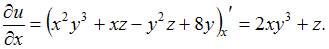
4. Частная производная 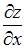функции 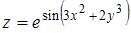имеет вид …

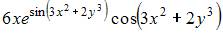- правильно

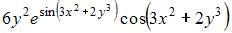
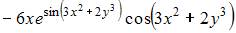
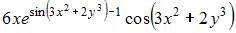
Решение:
При вычислении частной производной 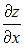по переменной 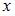переменную 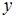рассматриваем как постоянную величину. Тогда

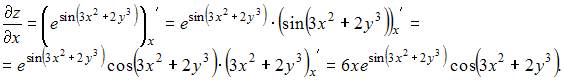
5. Частная производная 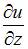функции 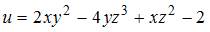имеет вид …

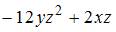- правильно

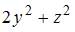
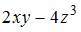
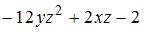
Решение:
При вычислении частной производной 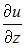по переменной 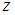переменные 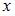и 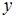рассматриваем как постоянные величины. Тогда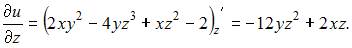

6. Значение частной производной 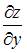функции 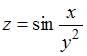в точке 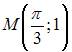равно …

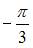- правильно

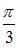
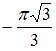
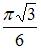
Решение:
При вычислении частной производной 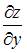по переменной 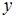переменную 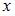рассматриваем как постоянную величину. Тогда

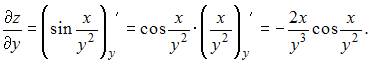
Следовательно,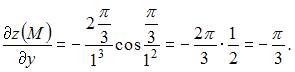

7. Значение частной производной 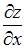функции 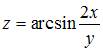в точке 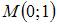равно …

– 2

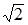
Тема 10: Частные производные высших порядков
1. Частная производная второго порядка 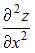функции 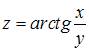имеет вид …

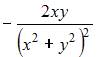- правильно

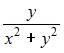
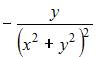
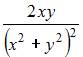
Решение:
При вычислении частной производной функции 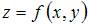по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
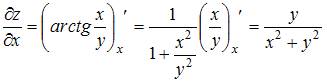и

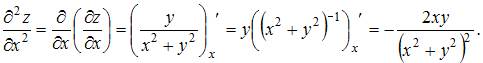
2. Частная производная второго порядка 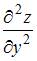функции 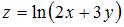имеет вид …

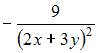- правильно

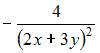
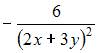
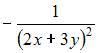
Решение:
При вычислении частной производной функции 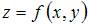по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда

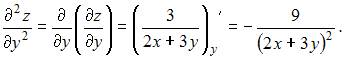
3. Смешанная частная производная второго порядка 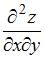функции 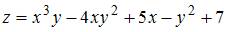имеет вид …

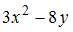- правильно

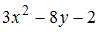
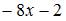
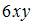
Решение:
При вычислении частной производной функции 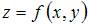по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда

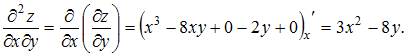
4. Частная производная второго порядка 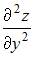функции 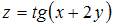имеет вид …

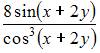- правильно

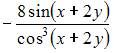
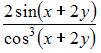
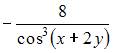
Решение:
При вычислении частной производной функции 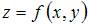по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда 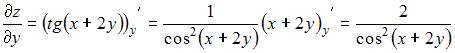и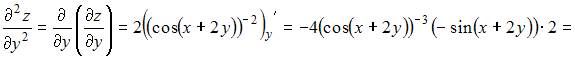

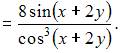
5. Дана функция 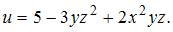Тогда производная 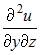равна …

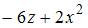- правильно

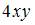
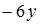
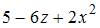
6. Частная производная второго порядка 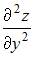функции 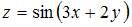имеет вид …

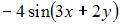- правильно

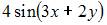
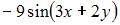
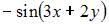
Решение:
При вычислении частной производной функции 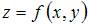по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
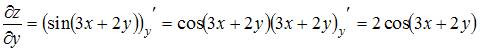и

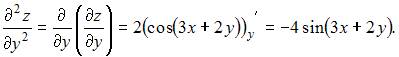
Тема 11: Полный дифференциал
1. Полный дифференциал функции 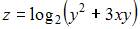имеет вид …

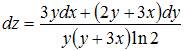- правильно

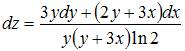
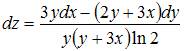
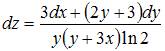
Решение:
Полный дифференциал функции нескольких переменных равен сумме произведений частных производных этой функции на дифференциалы соответствующих независимых переменных, то есть

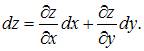
Тогда

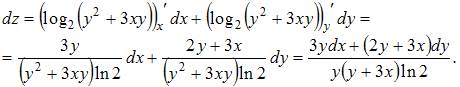
2. Полный дифференциал функции 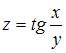имеет вид …

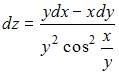- правильно

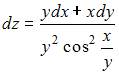
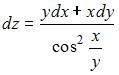
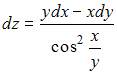
Решение:
Полный дифференциал функции нескольких переменных равен сумме произведений частных производных этой функции на дифференциалы соответствующих независимых переменных, то есть

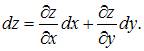
Тогда

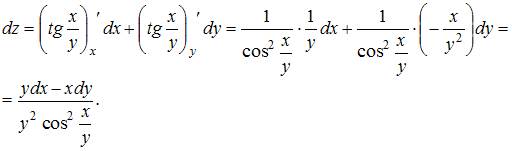
3. Приближенное значение функции 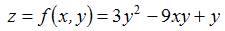в точке 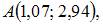вычисленное с помощью полного дифференциала, равно …

0,51

1,71

4,29

0,45

Решение:
Воспользуемся формулой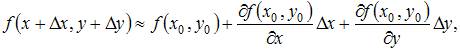
где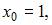
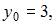
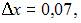
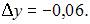
Вычислим последовательно



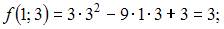
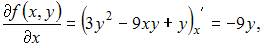
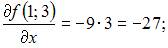
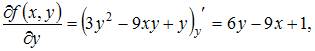
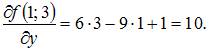
Тогда

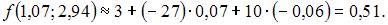
4. Полный дифференциал функции 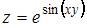имеет вид …