Кеңістіктегі салу есептерін шешу әдістері және салуға берілген есептерді шешуге мысалдар

Мектеп оқушыларының кеңістікті қабылдап, оны көз алдына елестете алуы стереометрияны оқытудың негізгі мәселелерінің бірі болып саналады. Осы айтылған мақсатты іс жүзіне асыруда кеңістіктегі салуға берілген есептерді шешудің зор мәні бар. Жазықтықтағы геометриялық салулар теориясы жеткілікті түрде талқыланып қарастырылады, ал стереометрияның әдістемелік мәселелеріне әлі де толық көңіл бөлінбей келеді. Геометриялық салулар теориясы - салуды негіздеу, есептерді кластарға жіктеу, есеп шешу әдістері, белгілі бір класқа жататын есептерді шешу критерийі, салу есептерін шешкенде барынша жай әдістерді тиімді қолдану сияқты мәселелерді қарастырады.

Кеңістіктегі салу есептерін кластарға жіктеу туралы әр түрлі көзқарастар мен тәсілдер бар. А.Н. Чалов кеңістіктегі салу есептерін геометриялық салуды орындау тәсілдері бойынша келесі топтарға бөледі:

1) елестету арқылы шешілетін есептер;

2) проекциялық сызбамен шешілетін есептер;

3) модельмен шешілетін есептер.

Салуға берілген стереометрия есептерін позициялық және метрикалық деп екі топқа бөлетіндер де бар. Негізгі элементтерінің қиылысуын ғана іздейтін, соны салумен аяқталатын есептер позициялық әдіспен шешілетін есептерге жатады. Кесінді салу, белгілі бір шамасы бар бұрышты салу, перпендикуляр тұрғызу, биссектриса жүргізу және т.б. белгілі шарттарды қанағаттандыратын фигура салу талабы қойылатын есептер метрикалық есептерге жатады. Мысалы, В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович өздерінің құрастырған «Математикалық есептер шешу практикумында» кеңістіктегі салуға берілген есептерді мынадай әдістер бойынша топтарға бөледі:

1) кеңістіктегі қарапайым салулар;

2) нүктелердің геометриялық орындары;

3) кейбір нүктелердің геометриялық орындары мен түзулерді пайдалану;

4) кескіндеу арқылы салу.

Салуға берілген стереометрия есептері талдау, салу, дәлелдеу және зерттеу сияқты төрт кезеңнен тұрады.

Талдау - бір бүтінді, құрамды бөліктерге жіктейтін, әр бөлікті жеке қарастыратын зерттеу әдісі. Ол салу есебін шешудің жоспарын табуға мүмкіндік тудырады. Талдау - есеп шешудің барынша маңызды кезеңі. Есепке дұрыс жүргізілген талдау - есепті шешу жоспарын дұрыс құрастырудың кепілі. Салу есебіне талдау жасағанда сызба басты рөл атқарады. Сонда есеп шартын, сызбадағы элементтердің өзара орналасуына барынша басынан аяғына дейін талдау жасалады, есеп шартында берілгендер мен іздеген элементтер арасында байланыс орнатылады.

Есептің салу кезеңінде салу есебіне қолданылатын аксиомаларды, теоремаларды, қосымша қарапайым салуларды дәл көрсету керек.

Дәлелдеу кезеңі есеп шешімінің дұрыстығына күдік туғанда қажет болады. Салу есебін зерттеу кезеңінің өзіндік маңызды ерекшелігі бар. Ол қандай шарттар орындалғанда есептің шешуі бар болады және неше шешімі бар деген сұрақтарға жауап береді. Сонымен бірге зерттеу кезеңі кеңістік елесті дамытуға мүмкіндік туғызады.

Салуға берілген алғашқы есепті шығарғанның өзінде есепті шешудің кезеңдерін (талдау, салу, дәлелдеу, зерттеу) дәл анықтап бөлу керек.

Кеңістіктегі салуға берілген есептерді шешудің негізгі әдістері: аксиоматикалық әдіс, проективтік әдіс, геометриялық орындар әдісі.

Аксиоматикалық әдістің негізгі мәні есепті шешу кезінде салудың өзі орындалмайды, салуға берілген есеп элементар салуларға келтіріледі, кейін бұлардың бәрін бірге қарастыруға болатындай түрдегі барлық жай амалдар қарастырылады. Салу есебінде көрсетілген амалдар кейде аксиомалар деп, ал есепті шешу әдісі аксиоматикалық әдіс деп аталады. Себебі есепке қолданылатын барлық амалдар елестеу арқылы формальды түрде жүргізіледі де логикалық түрде негізделеді, мұндай әдіс формальды - логикалық әдіс деп те аталады. Әдетте логикалық ой тұжырымдары сызба арқылы жүргізіледі. Бұл есеп шешімін барынша жеңілдетеді: ойды іске қосады, көптеген геометриялық элементтер мен олардың жиынын есте сақтап қалуға, кеңістік жөнінде дұрыс түсінік орнығып қалыптасуына мүмкіндік берді. Аксиоматикалық әдіс оқушылар санасында кеңістік туралы түсініктің, логикалық ойлаудың дамуына барынша терең және берік теориялық білім алуға, әсіресе белгілі бір салуларға түсінік беретін стереометрияның алғашқы теоремаларын үйренуге мүмкіндік туғызады. Есептер шешу кезінде алдымен көрнекі құралдар - жазықтықтар моделі (нұсқасы), нүктелер мен түзулерді мақсатты түрде қолдану пайдасы зор. Осындай әдістер көмегімен салудың талаптары айқын түрде көрсетіледі, бұдан соң логикалық түрде негіздеу және логикалық негізде салынған кескінді салу дәлелденеді. Модельдеу есеп шешімін көрнекі түрде талдау жасауға, талдауды ықшамдауға мүмкіндік береді [17].

Проективтік әдіс (проекциялық сызбада салу есебін шешу әдісі).

Егер ерекше проекциялау ережесі бойынша геометриялық денелердің кескінін пайдалануға мүмкіндік болса, онда ол есепті сызбалық құралдың көмегімен барлық салу жұмысын орындауға болады. Мұндай кескін геометриялық денені бір жазықтыққа проекциялау жолымен алынады және проекциялық сызба деп аталады, ал есепті шешу әдісін «проекциялық сызбада салынатын есеп» деп атайды.

Кеңістіктегі салу есептерін шешуге барынша ынғайлы әдіс - еркімізше алынатын параллель проекциялау. Ол сызбаның көрнекілігімен, оны салудың өте жай қарапайым болатынымен сипатталады. Проекциялық сызба арқылы шешілетін салу есептері төрт кезеңнен тұрады. Бірақ барлық кезеңдерді әр есепте түгел іске асыру талабы қойылмайды.

Геометриялық орындар әдісі.

Кеңістікте элементтердің геометриялық орындарын табуға берілген кез келген есепті салу есебі ретінде тұжырымдауға болады. Кеңістіктегі геометриялық орындар әдісімен салуға берілген есептерді шешудің мәні төмендегі мәселелер арқылы сипатталады. Әуелі есептегі берілген шарттардың біреуінен басқасын ескерусіз қалдыра тұрамыз. Өзіміз әдейі таңдап алып қалаған бір ғана шартты қанағаттандыратын нүктелер жиынын қарастырамыз. Бұдан әрі есептің екінші шартын қанағаттандыратын нүктелер жиыны қарастырылады және т.с.с. Біз қарастырған барлық жиындардың қиылысуы есептің шешімі болады. Кеңістіктегі салу есептерін шешудің тек төрт әдісін қарастырдық. Кеңістікте салуға берілген есептерді шешудің басқа да әдістері бар. Есептер шешудің бір немесе басқа әдісін таңдап алу шешілуге тиісті есептің сипатына, есеп шығарушының дайындық дәрежесіне, т.б. байланысты. Күрделі есептерді шешу кезінде көбінесе бір мезгілде бірнеше әдіс қатарынан қолданылады [31].

Кеңістіктегі салуға берілген есептерді шешуге мысалдар қарастырайық.

48-мысал. Берілген а және b түзулеріне паралелль, берілген А нүктесінен өтетін жазықтық жүргізу керек.

Талдау. Іздеген жазықтық а түзуіне паралелль а түзуі арқылы өтуі керек. Дәл осы сияқты іздеген жазықтық b түзуіне паралелль b _х түзуі арқылы өтуі керек. а_х және b _х түзулері А нүктесі арқылы өтуі керек.

Салу. 1. А нүктесі және а түзуі арқылы 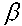жазықтығын жүргіземіз.

2. 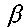жазықтығында А нүктесі арқылы а түзуіне паралелль а_х түзуін жүргіземіз.

3. А нүктесі және b түзуі арқылы 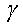жазықтығын жүргіземіз.

4. 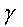жазықтығында А нүктесі арқылы b түзуіне паралелль b_х түзуін жүргіземіз.

5.а және b түзулерінен бір-бірден М және N нүктелерін таңдап аламыз.

6. А, М, N нүктелері арқылы іздеген ^а жазықтығын жүргіземіз.

Дәлелдеу. 1. Салуымыз бойынша 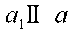және а_х sa. яғни, .

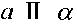2. 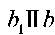-бұл салуымыз бойынша және 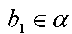. Демек, .

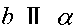3. A е а және 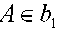. сонда, .

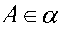Зерттеу. А нүктесінің а немесе b түзулерінде жатуына тәуелсіз есептің әрқашан шешімі болады. Егер а мен b түзулері паралелль болмаса, онда есептің бір ғана шешімі бар болады. Ал 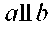болса, онда есептің сансыз көп шешуі бар болады.

49-мысал. Берілген түзуден тысқары жатқан нүкте арқылы, осы түзуге перпендикуляр жазықтық жүргізу.

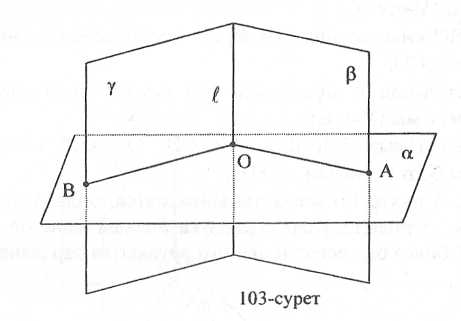
Шешуі. l түзуі және одан тысқары жатқан А нүктесі берілсін. A нүктесі арқылы өтіп l түзуіне перпендикуляр болатын α жазықтығын жүргізу керек (78-сурет).

Талдау. А нүктесі арқылы өтіп l түзуіне перпендикуляр болатын αжазықтығы жүргізілген болсын. Онда α жазықтығы l түзуін бір О нүктесінде қиятын және оған перпендикуляр болатын AO, ОВ түзулері арқылы өтеді. Қиылысатын l және АО түзулері - β жазықтығын, қиылысатын l және ОВ түзулері - ү жазықтығын анықтайды. Олай болса, салуды осы жазықтықтарды жүргізуден бастаймыз.

Салу. Берілген l түзуі мен одан тысқары жатқан А нүктесі арқылы β жазықтығын жүргіземіз және l түзуі арқылы р жазықтығымен беттеспейтін кез келген ү жазықтығын жүргіземіз. β жазықтығында А нүктесінен l түзуіне перпендикуляр АО түзуін жүргіземіз және ү жазықтығында О нүктесінен l түзуіне перпендикуляр ОВ түзуін тұрғызамыз.

Сурет-78

Қиылысатын АО және ОВ түзулері ізделінді α жазықтығын анықтайды. Дәлелдеу. Салуымыз бойынша l ┴ ОА, l ┴OB болғандықтан О нүктесінде қиылысатын ОА, ОВ түзулері арқылы өтетін α жазықтығы да l түзуіне

перпендикуляр және ОАсα болғандықтан А€α. Олай болса α ізделінді жазықтық.

Зерттеу. Егер А нүктесі l түзуінде жатса, онда А нүктесі арқылы l түзуіне перпендикуляр кез келген екі түзу тұрғызуға болады. Ол түзулер ізделінді α жазықтығын анықтайды. Олай болса бұл есептің әр уақытта шешімі бар және ол жалғыз болады.

50-мысал.Жазықтықтан тысқары жатқан нүкте арқылы жазықтыққа перпендикуляр түзу жүргізу.

Шешуі. α жазықтығы мен одан тысқары А нүктесі берілсін. A нүктесі арқылы α жазықтығына перпендикуляр түзу жүргізу қажет болсын. Бүл есепті екі түрлі әдіспен шығарайық.

1-тәсіл. Талдау. α жазықтығына перпендикуляр АО түзуі жүргізілген болсын. Онда үш перпендикуляр туралы теоремаға сәйкес, АВ көлбеуі және оның проекциясы ОВ бір мезгілде α жазықтығында жатқан қандайда бір CD түзуіне перпендикуляр болуы қажетті әрі жеткілікті. Мұндағы А нүктесі мен CD түзуі β жазықтығын анықтайды, ал қиылысатын АВ және ОВ түзулері ү жазықтығын анықтайды.

Салу.

1) α жазықтығында (79-сурет) кез келген CD түзуін жүргіземіз.

2) А нүктесі мен CD түзуі арқылы β жазықтығын жүргіземіз.

3) Осы β жазықтығында А нүктесінен CD түзуіне АВ перпендикулярын түсіреміз.

4) α жазықтығында В нүктесінен CD түзуіне ВО перпендикулярын ' тұрғызамыз.

5) АВ және ВО қиылысушы түзулері ү жазықтығын анықтайды және ү_┴CD.

6) ү жазықтығында А нүктесінен ВО түзуіне перпендикуляр АО түзуін жүргіземіз.

Дәлелдеу. Салуымыз бойынша AB┴CD, OB┴CD және АО┴ВО, CDcα, BOcα болғандықтан AO┴α.

Зерттеу. Егер А нүктесі α жазықтығында жатса, онда А нүктесінен α жазықтығына перпендикуляр тұрғызуға болады және ол біреу ғана болады. Олай болса бүл есептің шешімі әруақытта бар және жалғыз.

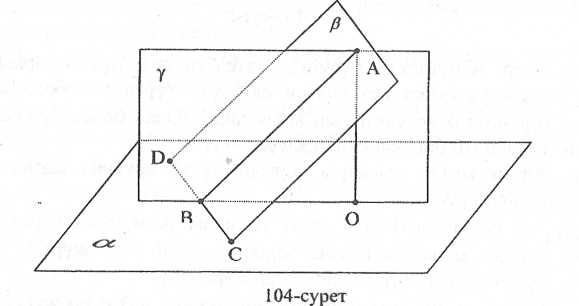Сурет-79

2-тәсіл. Талдау. А нүктесі арқылы α жазықтығына перпендикуляр а түзуі жүргізілген болсын (80-сурет). Онда бүл а түзуі α жазықтығына перпендикуляр басқа кез келген l түзуіне параллель болады. Ал l түзуі α жазықтығында жатқан кез келген қиылысушы b, с екі түзуіне перпендикуляр болуы қажет. l түзуі арқылы b түзуіне перпендикуляр β және с түзуіне перпендикуляр ү жазықтықтарын жүргізуге болады. Яғни l түзуі осы β және ү жазықтықтарының қиылысу сызығы болып табылады.

Салу. 1) а жазықтығында кез келген О нүктесінде қиылысатын b,с түзулерін аламыз.

2) О нүктесі арқылы b және с түзулеріне сәйкесінше перпендикуляр болатын β және ү жазықтықтарын жүргіземіз (1-есептегі тәсіл пайдаланылады). Олардың қиылысу сызығы l ┴ α болады.

3) l түзуі мен А нүктесі арқылы ∆ жазықтығын жүргіземіз.

∆ жазықтығында А нүктесі арқылы l түзуіне параллель а түзуін жүргіземіз.

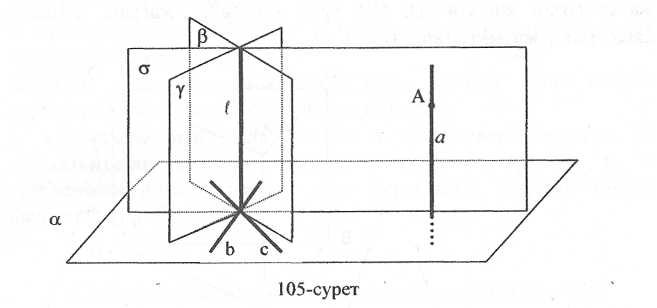Сурет-80

Дәлелдеу. Салуымыз бойынша b, с түзулері α жазықтығында жатыр. β┴b, ү┴с жазықтықтарының қиылысу сызығы l түзуі де бүл түзулердің әрбіріне перпендикуляр, яғни l ┴ b, l ┴ с. Олай болса l түзуі α жазықтығына да перпендикуляр. Ал а түзуі l түзуіне перпендикуляр болғандықтан, а түзуі де α жазықтығына перпендикуляр. а түзуі А нүктесі арқылы өтеді және α жазықтығына перпендикуляр, олай болса а ізделінді түзу.

Зерттеу. Осы есепті шығару 1-тәсілмен шығару жағдайына ұқсас орындалады. Көріп отырғанымыздай салу есебінде негізгі қиындық туғызатын талдау кезеңі болып табылады. Салу - талдау негізінде орындалатын болғандықтан, талдауды дұрыс жүргізу қажет.

Стереометриялық салу есептері негізінен стереометрия курсының алғашқы тарауларында кездесетіндіктен, салу есептеріне талдау жасауды кеңістікте “ілулі” фигуралар (түзулер, жазықтықтар) арқылы түсіндірген оқушыларға түсініксіз. Өйткені, оны елестету қиын. Сондықтан ол түзулер мен жазықтықтарды қандайда бір кеңістік денелеріне келтірілген моделдер немесе олардың кескіні арқылы көрсеткен дұрыс [31].

Мысалы, 1-мысалдың шығарылу жолын талдау үшін кез келген тік призманы пайдалануға болады. Нақтылық үшін АОВА₁О₁В₁ үшбұрышты тік призмасын алайық (81-сурет). ОО₁ қырын қамтитын түзуді - l, АОВ табан жағын қамтитын жазықтықты α деп белгілейік. Мұндағы l ┴ α болғандықтан түзу мен жазықтықтың перпендикулярлық шартына сәйкес OA ┴ l, OB ┴ l болады. l түзуі мен одан тысқары жатқан А нүктесі АОО₁А₁ жағын қамтитын β жазықтығын анықтайды. ОВ түзуі OBВ₁О₁ жағына немесе оны қамтитын ү жазықтығына тиісті.

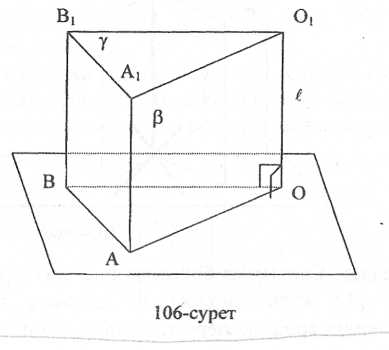
Сурет-81

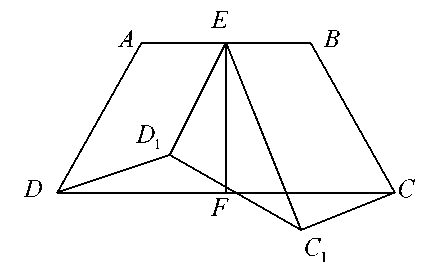
51-мысал. Барлық төрт қабырғасы және қарама-қарсы екі қабырғасының орталарын қосатын кесінді берілген жағдайда ABCD төртбұрышын салу керек

Шешуі. ABCD — ізделген төртбұрыш, EF — АВ және DC қабырғаларының орталарын қосатын кесінді болсын. AD қабырғасын параллель жылжытып ED_Y және ВС қабырғасын параллель жылжытып EC_Y жағдайына келтіреміз, сонда DD = AE, DDj AE; CC = BE, CCj BE, DF = CF— бұлар шарт бойынша, демек, 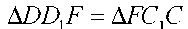(екі қабырғасы және олардың арасындағы бұрышы бойынша тең).

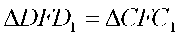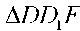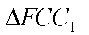Бұл үшбұрыштардың теңдігінен шығады. Демек, Д, F және C — нүктелері бір түзудің бойында жатады. D_XEC_X үшбұрышында екі қабырғасы мен үшінші медианасы белгілі болғанда оны салуға болады. Бұдан соң үш қабырғасы бойынша және үшбұрыштарын салып, DAED_X, және BECC параллелограмдарын салуға болады. Бұдан соң A және В нүктелері анықталады.

82-сурет.

Салу. DEC үшбұрышын D_YE = AD және CE = BC, сондай-ақ EF медианасы бойынша саламыз. Бүл үшін ең алдымен 2EF, ED, EC_X, үш қабырғасы бойынша үшбұрыш салып, оны параллелограмға дейін толықтырамыз. Осы параллелограмның жартысы DEC — үшбұрышы болады. Қабырғалары 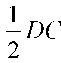және

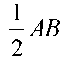болатын өзара тең үшбұрыштар D_XF және FC кесінділеріне салынады. Бұлар арқылы D және С нүктелерін саламыз. DAED_l және BECC параллелограмдарын салып, А және В нүктелерін табамыз.

Дәлелдеу. ABCD төртбұрышы — ізделген төртбұрыш, себебі ол есептің барлық шарттарын қанағаттандырады. DF және FC бір түзудің бойында жатыр, себебі 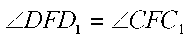және DF_l және CF бір түзудің бойында жатыр.

Зерттеу. ED_YC үшбұрышын салу үшін 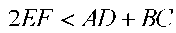және

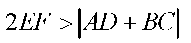шарттарының орындалуы қажетті, ал 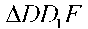және —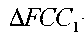

салу үшін 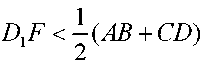және 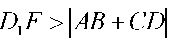шарттары орындалуы қажетті. Егер бүл шарттар орындалса, онда есептің бір ғана шешімі бар болады.

52-мысал.α және β жазықтықтары параллель, α жазықтығында жатқан А нүктесі арқылы β жазықтығына параллель а түзуі жүргізілген. Осы а түзуінің α жазықтығында жататынын дәлелде.

Шешуі. А түзуі β жазықтығына тиісті В нүктесі арқылы ү жазықтығын жүргіземіз (83-сурет). Ол жазықтық α және β жазықтықтарын сәйкес параллель а₁ және b түзулері бойымен қияды. а₁ түзуін қарастырайық. Ол А нүктесі арқылы

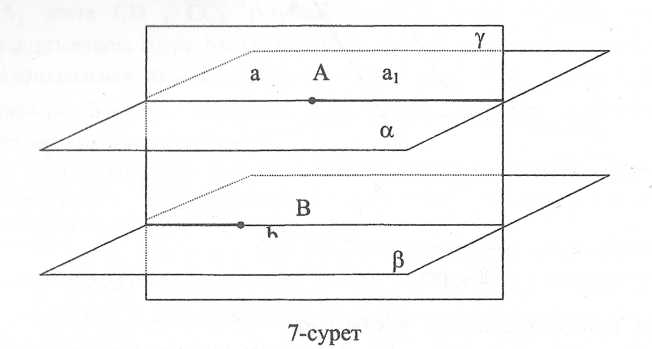
Сурет-83

өтеді және α жазықтығында жатады, яғни дәлелдеу қажетті қасиетке ие. Содан кейін, есеп а₁ мен а түзулері сәйкес келетінін дәлелдеуге келтіріледі. Бұл есептердің екеуі де қарапайым [31].