Занятие 17. Преобразование координат и упрощение уравнений кривых второго порядка

17.1. Преобразование координат.

Перейдем от системы координат Оху к новой системе 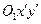(направление осей координат прежнее, за новое начало координат принята точка 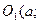b)). Связь между старыми и новыми координатами некоторой точки М плоскости определяется следующими формулами:

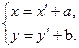или

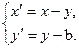
Первая пара формул дает выражение старых координат через новые, вторая-выражение новых координат через старые. При повороте осей координат на угол 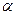(начало координат прежнее, причем 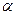отсчитывается против часовой стрелки) зависимость между старыми координатами ( х, у) и новыми ( 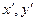) определяется следующими формулами:

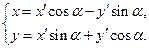
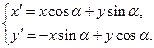
Пример 17.1.Сделан параллельный перенос осей координат, причем новое начало расположено в точке 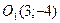. Известны старые координаты точки 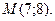Определить новые координаты этой точки.

Решение. Здесь 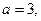b=-4, х=7, у=8.

Так как 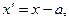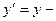b, то 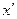=7-3=4, 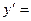8-(-4)=12.

Пример 17.2На плоскости Оху дана точка М(4;3). Систему координат повернули вокруг начала координат так, что новая ось прошла через точку М. Определить старые координаты точки А, если известны ее новые координаты ,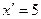

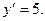
Решение. Так как 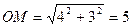, то sin 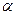= 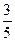, cos 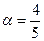; получаем формулы преобразования координат:

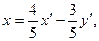
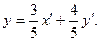
Положив 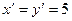, находим х=1, у=7.

Пример 17.3.Привести уравнение кривой к каноническому виду

.

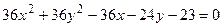Решение.Выделяя полные квадраты, преобразуем левую часть уравнения. Имеем

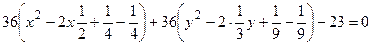или

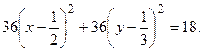Вводя новые координаты 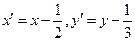, после деления на 18, получаем 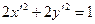или .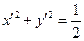

Таким образом, получено уравнение окружности с центром в точке .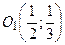

Пример 17.4.Привести уравнение кривой к каноническому виду и построить линию, определяемую уравнением .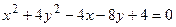

Решение.Выделяя полные квадраты , преобразуем левую часть уравнения. Имеем

;

;

.

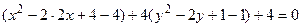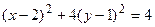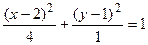Вводя новые координаты 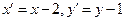, получаем .

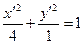Таким образом, получено уравнение эллипса с центром в точке .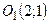

Пример 17.5.Привести уравнение кривой к каноническому виду и построить линию, определяемую уравнением .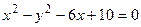

Решение.Выделяя полные квадраты , преобразуем левую часть уравнения. Имеем

;

.

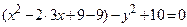
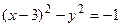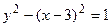Вводя новые координаты 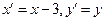, получаем 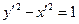- уравнение гиперболы, для которой действительной осью является ось 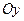, а центр расположен в точке .

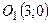Пример 17.6.Привести уравнение кривой к каноническому виду и построить линию, определяемую уравнением .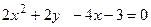

Решение.Выделяя полный квадрат, преобразуем левую часть уравнения. Имеем

;

;

.

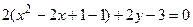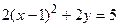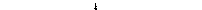
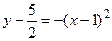Вводя новые координаты

,

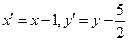получаем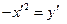

Это уравнение параболы, вершина которой в точке .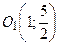

Пример 17.7.Привести к каноническому виду уравнение

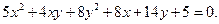
Решение. 1). Преобразуем это уравнение, воспользовавшись формулами поворота осей координат

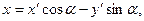
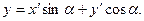
Имеем

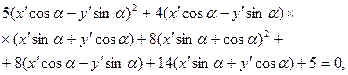
или

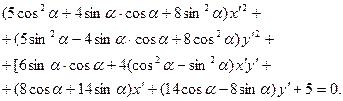
Найдём 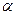из условия

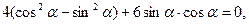
т.е. приравниваем нулю коэффициент при 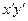. Получаем

уравнение 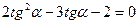.Отсюда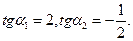

Заметим, что эти значения 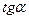соответствуют двум взаимно перпендикулярным направлениям. Поэтому, беря 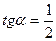вместо 2, мы только меняем ролями ос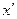и и .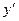

Пусть 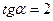, тогда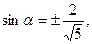 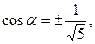возьмём положительные значения 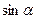и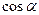

Тогда уравнение принимает вид

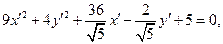
или

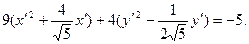
2) Выражение в скобках дополним до полных квадратов:

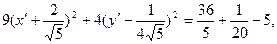
или

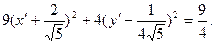
Приняв за новое начало точку 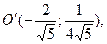применим формулы преобразования координат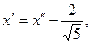 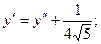получим 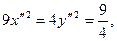или 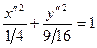(уравнение эллипса).

Пример 17.8.Привести к каноническому виду уравнение

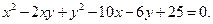
Решение. 1). Преобразуем это уравнение, воспользовавшись формулами поворота осей координат

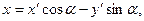
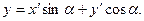
Имеем

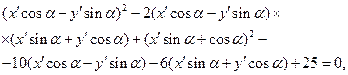
или

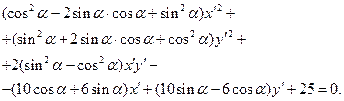
Приравнивая нулю коэффициент при 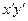, получаем уравнение 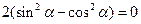, откуда 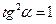, т.е.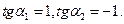

Пусть 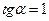, тогда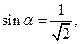 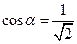. Тогда уравнение принимает вид

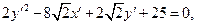
или

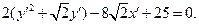
2) Выражение в скобках дополним до полного квадрата:

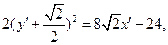или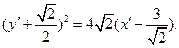

Приняв за новое начало, точку 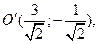применим формулы преобразования координат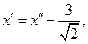 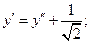получим 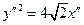(уравнение параболы).

Вопросы для самопроверки

4. Каковы канонические уравнения эллипса, гиперболы, параболы?

5. Что называется фокусами, директрисами и эксцентриситетом эллипса, гиперболы, параболы?

6. Каковы геометрические свойства эллипса, гиперболы, параболы?

7. Что называется асимптотами гиперболы?

8. Каков геометрический смысл неравенства первой степени с двумя переменными?