Базис и размерность линейного пространства
Определение. Базисом линейного пространства  называется линейно независимая система векторов
называется линейно независимая система векторов 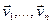 из
из  такая, что любой вектор из пространства
такая, что любой вектор из пространства  можнопредставить в виде линейной комбинации векторов
можнопредставить в виде линейной комбинации векторов 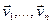 .
.
Определение. Размерностью линейного пространства  называется количество векторов в базисе этого пространства. Обозначается
называется количество векторов в базисе этого пространства. Обозначается 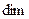
 .
.
Утверждение. Базисом линейного пространства решений однородной системы является ее фундаментальная система решений.
Утверждение. 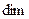 Rn=n.
Rn=n.
Примеры
1. Образуют ли базис в пространстве R3 векторы
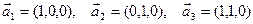 ?
?
Решение. По определению базис составляют линейно независимые векторы. Линейная зависимость (или независимость) определяется исходя из анализа равенства нулю линейной комбинации этих векторов:
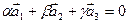 .
.
Последнее векторное уравнение после записи его по компонентам представляет собой систему трёх однородных уравнений относительно 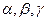 . Согласно схеме исследования линейной зависимости векторов (см. пример 1 из раздела «Линейная зависимость и независимость векторов») вычислим определитель матрицы, составленной из координат векторов
. Согласно схеме исследования линейной зависимости векторов (см. пример 1 из раздела «Линейная зависимость и независимость векторов») вычислим определитель матрицы, составленной из координат векторов
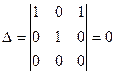
Определитель системы равен нулю, следовательно, она имеет нетривиальное решение и это означает, что исходная группа векторов линейно зависима и не образует базис в R3.
2. Найти размерность и один из базисов линейного пространства решений однородной системы:
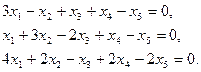
Решение. Представленная система состоит из трёх уравнений и содержит 5 неизвестных. Выпишем матрицу системы и упростим её с помощью элементарных преобразований, сначала поменяв местами строки 1 и 2, а затем вычитая новую первую строку, умноженную на 3 и 4, соответственно из второй и третьей строк :
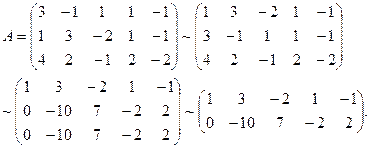
Видно что ранг матрицы 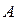 равен 2. Следовательно, две неизвестные являются главными, а три - свободными. Значит ФСР системы содержит 5-2=3 линейно независимых решения. Выберем в качестве главных
равен 2. Следовательно, две неизвестные являются главными, а три - свободными. Значит ФСР системы содержит 5-2=3 линейно независимых решения. Выберем в качестве главных 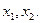 . Это можно сделать, т.к. минор 2-го порядка, составленный из коэффициентов при этих неизвестных, отличен от нуля. Система, соответствующая преобразованной матрице, имеет вид
. Это можно сделать, т.к. минор 2-го порядка, составленный из коэффициентов при этих неизвестных, отличен от нуля. Система, соответствующая преобразованной матрице, имеет вид
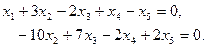
Отсюда, выражая главные неизвестные через свободные, получим общее решение
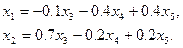
Или иначе:
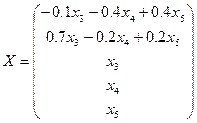 .
.
Фундаментальная совокупность решений, составленная в соответствии с изложенным алгоритмом (см. пример 4 в разделе «Системы линейных алгебраических уравнений»), является базисом линейного пространства решений исходной системы и в данном случае имеет вид
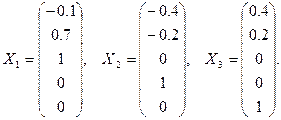
Размерность искомого пространства равна 3.
Задачи
3.19. Является ли базисом пространства R3 система векторов:
а) 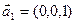 ,
, 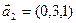 ,
, 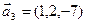 ;
;
б) 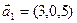 ,
, 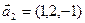 ;
;
в) 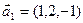 ,
, 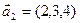 ,
, 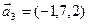 ,
, 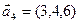 .
.
3.20. Найти размерность и базис пространства решений однородной системы:
а) 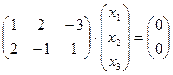 ; б)
; б) 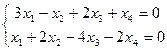 ;
;
в) 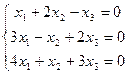 ; г)
; г) 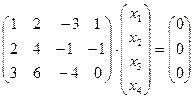 ;
;
д) 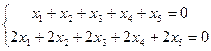 .
.
3.21. Найти размерность и указать какой-либо базис пространства всех векторов, выходящих из начала координат и:
а) лежащих на прямой 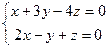 ;
;
б) перпендикулярных прямой 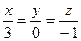 ;
;
в) лежащих в плоскости 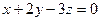 ;
;
г) перпендикулярных плоскости 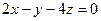 .
.
3.22. Вектор 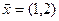 разложить по базису
разложить по базису 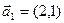 ,
, 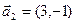 .
.
3.23. Данный вектор 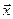 разложить по указанному базису
разложить по указанному базису 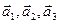 :
:
а) 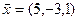 ,
, 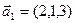 ,
, 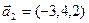 ,
, 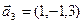 ;
;
б) 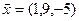 ,
, 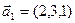 ,
, 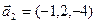 ,
, 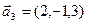 .
.
3.24. Дополнить до какого-либо базиса соответствующего пространства Rn систему:
а) 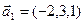 ,
, 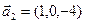 ;
;
б) 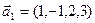 ,
, 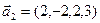 ,
, 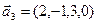 ;
;
в) 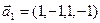 ,
, 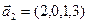 .
.
3.25. При каких значениях параметра 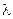 векторы образуют базис пространства R3:
векторы образуют базис пространства R3:
а) 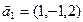 ,
, 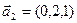 ,
, 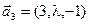 ;
;
б) 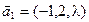 ,
, 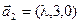 ,
, 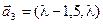 ;
;
в) 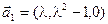 ,
, 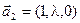 ,
, 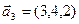 .
.
3.26. Найти размерность и указать какой-либо базис пространства:
а) многочленов степени не выше n;
б) квадратных матриц порядка n;
в) прямоугольных матриц размера 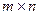 ;
;
г) симметричных матриц порядкаn;
д) диагональных матриц порядкаn.
3.27. Доказать, что система 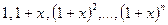 образует базис
образует базис
пространства многочленов степени не выше n.
3.28. Найти размерность и указать какой-либо базис пространства положительных чисел, в котором сумма произвольных чисел 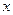 и
и 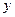 вычисляется как
вычисляется как 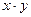 , а произведение вещественного числа
, а произведение вещественного числа 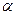 на произвольное положительное число
на произвольное положительное число 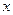 вычисляется как
вычисляется как 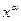 .
.
Координаты вектора
Определение. Координатами вектора 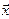 в базисе
в базисе 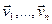 называются числа
называются числа 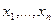 , при которых выполняется равенство
, при которых выполняется равенство 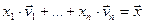 .
.
Определение. Матрицей перехода от базиса 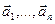 к базису
к базису 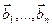 называется матрица вида
называется матрица вида
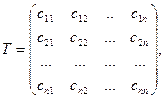
где для каждого 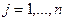 в
в 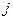 -ом столбце стоят координаты
-ом столбце стоят координаты 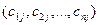 вектора
вектора 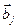 в базисе
в базисе 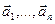 .
.
Утверждение. Координаты 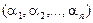 вектора
вектора 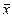 в базисе
в базисе 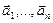 и координаты
и координаты 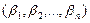 этого же вектора в базисе
этого же вектора в базисе 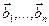 связаны равенством
связаны равенством
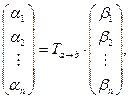
где 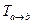 - матрица перехода от базиса
- матрица перехода от базиса 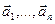 к базису
к базису 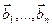 .
.
Утверждение. Матрица перехода 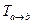 от базиса
от базиса 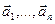 к базису
к базису 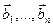 и матрица обратного перехода
и матрица обратного перехода 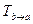 от базиса
от базиса 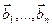 к базису
к базису 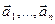 связаны равенством
связаны равенством 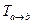 =
= 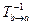 .
.
Примеры
1. Найти координаты вектора 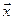 в базисе
в базисе 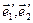 , если известно
, если известно
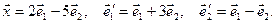
Решение. В соответствии с определением матрица перехода от базиса 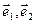 к базису
к базису 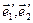 есть
есть
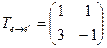 .
.
Обозначим координаты вектора 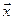 в базисе
в базисе 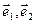 через
через 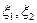 , а в базисе
, а в базисе 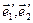 через
через 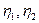 . Искомые координаты
. Искомые координаты 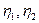 связаны с известными координатами
связаны с известными координатами 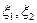 следующим соотношением:
следующим соотношением:
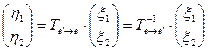 .
.
Видно, что для получения координат 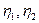 необходимо вычислить матрицу, обратную
необходимо вычислить матрицу, обратную 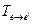 . Используя стандартную процедуру (см. пример 1 из подраздела «Обратная матрица»), имеем
. Используя стандартную процедуру (см. пример 1 из подраздела «Обратная матрица»), имеем
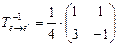 .
.
Вычислим теперь координаты 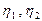 :
: 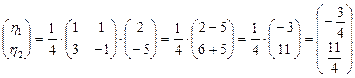 .
.
3. Найти матрицу перехода от базиса 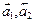 к базису
к базису 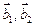 по
по
данным разложениям этих векторов в базисе 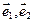 :
:
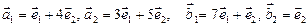 .
.
Решение. Чтобы построить матрицу 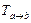 перехода от базиса
перехода от базиса 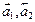 к базису
к базису 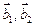 , необходимо найти разложение векторов
, необходимо найти разложение векторов 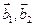 по базису
по базису 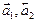 . Сделаем это, представив
. Сделаем это, представив 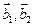 в виде разложения по
в виде разложения по 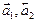 с неизвестными координатами, которые требуется определить:
с неизвестными координатами, которые требуется определить:
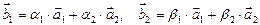 ,
,
или с учётом вида этих векторов в базисе 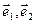
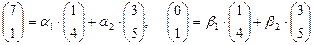 .
.
Откуда для координат 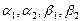 имеем
имеем 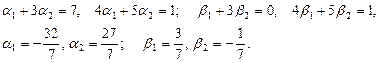
Теперь, зная разложение 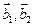 по
по 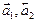 , выпишем матрицу
, выпишем матрицу 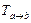 :
:
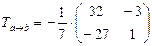 .
.
Задачи
3.29. Найти координаты вектора 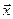 в базисе
в базисе 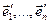 , если известны следующие разложения по базисам
, если известны следующие разложения по базисам 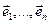 и
и 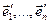 :
:
а) 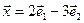 ,
, 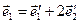 ,
, 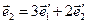 ;
;
б) 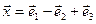 ,
, 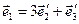 ,
, 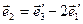 ,
, 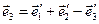 .
.
3.30. Пользуясь определением, найти координаты вектора 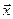 в указанном базисе
в указанном базисе 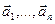 :
:
а) 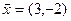 ,
, 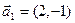 ,
, 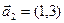 ;
;
б) 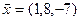 ,
, 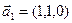 ,
, 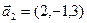 ,
, 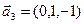 ;
;
3.31. Построить матрицу перехода 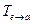 от базиса
от базиса 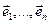 к базису
к базису 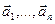 и матрицу обратного перехода, если векторы
и матрицу обратного перехода, если векторы 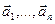 в базисе
в базисе 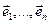 имеют координаты
имеют координаты
а) 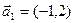 ,
, 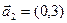 ;
;
б) 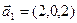 ,
, 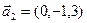 ,
, 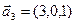 .
.
3.32. Найти матрицу перехода
а) от базиса 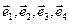 к базису
к базису 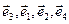 ;
;
б) от базиса 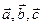 к базису
к базису 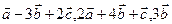 .
.
3.33. Дана матрица перехода
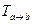 =
= 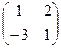
от базиса 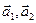 к базису
к базису 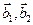 . Найти координаты вектора
. Найти координаты вектора
а) 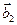 в базисе
в базисе 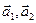 ; б)
; б) 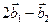 в базисе
в базисе 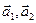 ;
;
в) 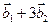 в базисе
в базисе 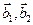 ; г)
; г) 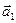 в базисе
в базисе 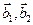 ;
;
д) 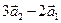 в базисе
в базисе 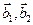 ; е)
; е) 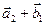 в базисе
в базисе 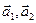 .
.
3.34. Используя матрицу перехода от базиса к базису, найти координаты вектора 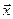 в базисе
в базисе 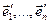 , если в базисе
, если в базисе 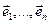
а) 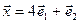 ,
, 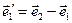 ,
, 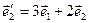 ;
;
б) 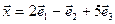 ,
, 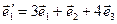 ,
, 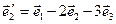 ,
, 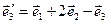 .
.
3.35. Построить матрицу перехода 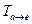 от базиса
от базиса 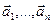 к базису
к базису 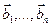 по данным разложениям векторов
по данным разложениям векторов 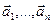 и
и 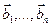 в базисе
в базисе 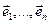 :
:
а) 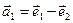 ,
, 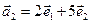 ,
, 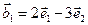 ,
, 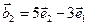 ;
;
б) 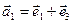 ,
, 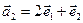 ,
, 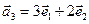 ,
, 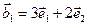 ,
, 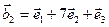 ,
, 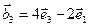 .
.
3.36. Построить матрицу перехода 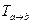 от базиса
от базиса 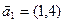 ,
, 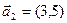 к базису
к базису 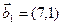 ,
, 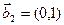 и матрицу обратного перехода
и матрицу обратного перехода 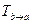 .
.
3.37. Построить матрицу перехода от базиса 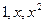 к базису
к базису 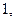
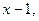
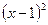 в пространстве многочленов степени не выше
в пространстве многочленов степени не выше 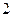 .
.
3.38. В пространстве многочленов степени не выше 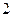 найти разложение вектора
найти разложение вектора 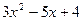 по базису
по базису 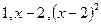 .
.
