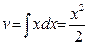Тема 3. Заміна змінної та інтегрування частинами у визначеному інтегралі

1. Заміна змінної у визначеному інтегралі.

2. Інтегрування частинами у визначеному інтегралі.

Короткі теоретичні відомості

Якщо функція 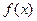неперервна на відрізку [a;b], а функція 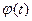неперервна разом зі своєю похідною 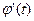на відрізку 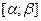, причому 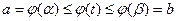для всіх 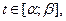то

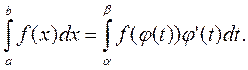(1)

Формула (1) називається формулою заміни змінної у визначеному інтегралі, або формулою інтегрування підстановкою.

Застосування формули (1) розглянемо на конкретних прикладах.

Приклад 1. Обчислити інтеграл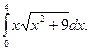

Розв’язання.

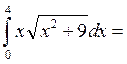
Відповідь: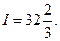

Приклад 2. Обчислити інтеграл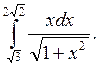

Розв’язання.

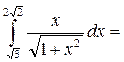
Відповідь:І = 1

Приклад 3. Обчислити інтеграл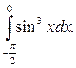

Розв’язання.

=

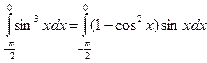Відповідь: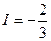

Якщо функці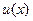ї і 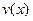неперервні разом зі своїми похідними 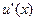та 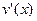на відрізку [a;b], то

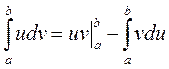(2)

Формула (2) називається формулою інтегрування частинами у визначеному інтегралі.

Застосування формули (2) розглянемо на конкретних прикладах.

Приклад 1. Обчислити інтеграл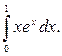

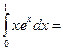
Розв’язання.

Відповідь:I = 1.

Приклад 2. Обчислити інтеграл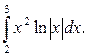

Розв’язання.

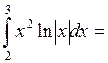
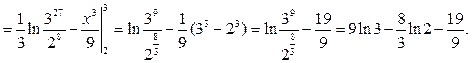
Відповідь: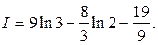

Приклад 3. Обчислити інтеграл .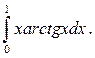

Розв’язання.

		=

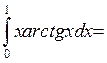
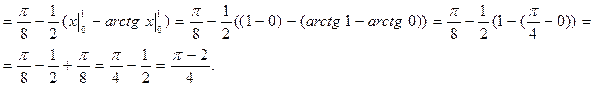
Відповідь: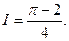

Питання для контролю вивченого матеріалу

1. Яку формулу використовують у визначеному інтегралі при заміні змінної?

2. Яку формулу використовують при інтегруванні частинами у визначеному інтегралі?

3. Обчислити інтеграли:

а)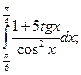

б)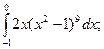

в)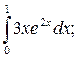

г)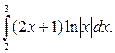

Література

1. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие. – 2-е изд., перераб. и доп. – М.: Наука, 1990. – 576 с.: ил.

2. Дюженкова Л.І., Носаль Т.В.: Вища математика: Практикум. – К.: Вища школа, 1991. – 407 с.: іл.

3. Соколенко О.І. Вища математика. – К.: Видавничий центр „Академія”, 2002. – 431с.

Тема 4. Об’єм тіла обертання.

1. Поняття тіла обертання.

2. Обчислення об’єму тіла обертання.

Короткі теоретичні відомості

Нехай маємо криволінійну трапецію Р(f), породжену графіком функції f, визначеної, невід’ємної і неперервної на відрізку [a;в]. Цю криволінійну трапецію як тверде тіло обертатимемо навколо осі Ох. Просторове тіло, яке опише при цьому криволінійна трапеція, називається тілом обертання.

Об’єм тіла, утвореного обертанням навколо осі ОХ криволінійної трапеції, обмеженої неперервною кривою y = f(x) і прямими х=а, х=в, y=0, обчислюється за формулою

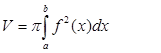(1)

Якщо навколо осі Ох обертається фігура, обмежена кривими y=f₁(x) і y=f₂(x), f₂(x) ≥ f₁(x) ≥0 і прямими х=а і х=b, то об’єм утвореного тіла обертання

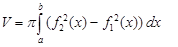(2)

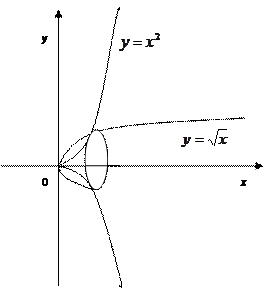Приклад. Обчислити об’єм тіла ,утвореного обертанням навколо осі Ох фігури, обмеженої кривими y=x² і y= .

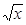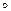Використаємо формулу (2), де .

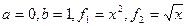Маємо:

.

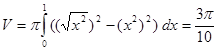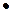
Питання для контролю вивченого матеріалу

1. Що таке тіло обертання ?

2. Записати формулу для обчислення об’єму тіла, обмеженого кривою y=f(x) і прямими x=a, x=b, y=0.

3. Як обчислюється об’єм тіла, обмеженого кривими y=f₁(x) і y=f₂(x), f₂(x) ≥ f₁(x) ≥ 0 і прямими x=а, x=в?

4. Обчислити об’єм тіла, утвореного обертанням навколо вісі Ох фігури, обмеженої лініями y=x³, y=0, x=0, x=2.

Література

1. Соколенко О.І. Вища математика: Підручник – К.: Видавничий центр „Академія”, 2002. – 432с.

2. Валуцэ И.И. Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие. – 2-е изд., перераб. и доп. – М.: Наука, 1990. – 576с.

3. Дюженкова Л.І., Носаль Т.В. Вища математика: Практикум: Навчальний посібник. – К.: Вища школа, 1991. – 407с.: іл.
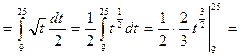
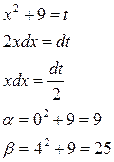
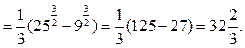
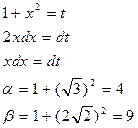
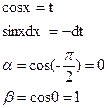
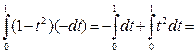
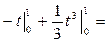
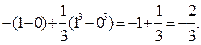
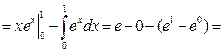
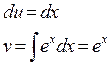
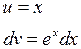
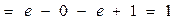
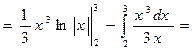
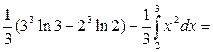
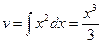
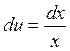
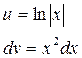
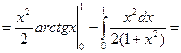
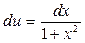
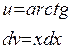
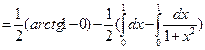