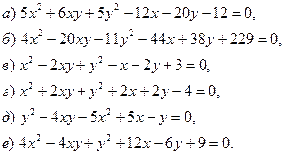Побудова ліній другого порядку за їх загальними рівняннями

Розглянемо в даному параграфі як побудувати лінію в системі координат, відносно якої вона задана загальним рівнянням.

Розглянемо це питання відносно кожного класу ліній окремо.

1. Побудова центральних ліній (еліпса та гіперболи). Нові осі координат, відносно яких еліпс та гіпербола задаються своїми канонічними рівняннями

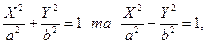
будуть осями симетрії, а початок координат – центром симетрії кривої. Таким чином, для побудови нової системи координат потрібно знайти:

1. Центр кривої.

2. Осі кривої.

Центр кривої, як ми бачили в § 5, визначається з рівнянь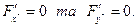

Для побудови осей кривої немає необхідності знаходити їх рівняння, простіше обчислити кут нахилу нової осі з формули:

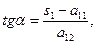
де s₁ – корінь характеристичного рівняння, який стоїть коефіцієнтом у вище наведеному рівнянні при X².

Вісь 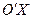проводиться через попередньо побудований центр під кутом α до старої осі Ох і вісь 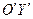- перпендикулярно до осі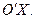

Далі виконується побудова кривої в новій системі координат за її канонічним рівнянням.

Приклад 1. Побудувати лінію

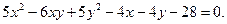
Розв’язання. 1. Обчислимо інваріанти:

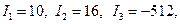
так як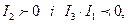

лінія буде еліпсом.

2. Розв’яжемо характеристичне рівняння

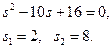
3. Запишемо приведене та канонічне рівняння даної лінії:

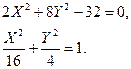
4. Знайдемо координати центру: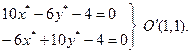

5. Визначимо кут нахилу осі 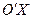до старої осі Ох:

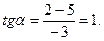
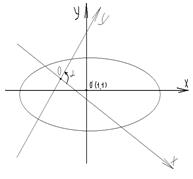
6. Побудуємо криву відносно початкової системи координат (мал.15).

2. Побудова параболи. Для побудови параболи необхідно знайти її вісь, вершину і напрям її віток вздовж осей симетрії.

В першу чергу знаходимо рівняння вісі параболи як діаметра, спряженого з перпендикулярними до нього хордами.

Так як кутовий коефіцієнт осі параболи нам відомий (§ 5(15) ):

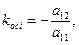
то кутовий коефіцієнт перпендикулярних до нього хорд буде рівним

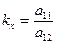
та рівняння осі запишеться у вигляді

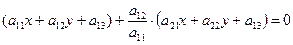
або

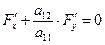
(§ 5(13) і ( )).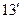

Знаючи тепер рівняння осі, можна знайти координати вершини параболи як точки перетину параболи з її віссю.

Для визначення напряму віток параболи вздовж її осі можна користуватися точками перетину параболи, заданої загальним рівнянням, з осями координат.

Побудуємо, таким чином, нову систему координат 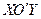і параболу в ній за її канонічним рівнянням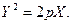

Покажемо тепер на осі 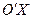(вісь параболи) позитивний напрямок у відповідності зі знаком коефіцієнта 2р. Позитивний напрям осі 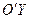отримуємо поворотом позитивного напряму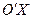

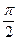Мал.15

на кут проти годинникової стрілки.

Приклад 2. Побудувати лінію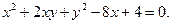

Розв’язок. 1. Підрахуємо інваріанти:

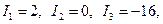
так як

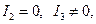
то лінія буде параболою.

2. Запишемо її зведене та канонічне рівняння:

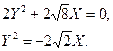
3. Знайдемо рівняння осі параболи:

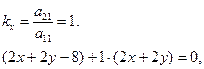
або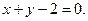
4. Визначимо координати вершини, для чого розв’яжемо дане рівняння лінії сумісно з рівнянням осі: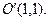

5. Знайдемо точки перетину параболи з осями координат, для чого розв’яжемо дане рівняння лінії поруч з рівнянням осей координат. Поклавши у=0, маємо х²-8х+4=0, звідки

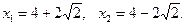
Поклавши х=0,маємо у²+4=0, звідки

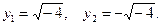
Таким чином парабола перетинає вісь Ох в точках

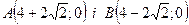
і не перетинає вісь Оу.

6. Побудуємо вершину параболи, її вісь та саму параболу в початковій системі координат. У відповідності з отриманим канонічним рівнянням відмітимо позитивні напрями на нових осях координат.

3. Побудова лінії другого порядку, яка розпалася на пару прямих. Якщо лінія другого порядку розпалася на пару паралельних прямих, що слідує з умови І₃=0, то ліва частина її загального рівняння повинна розкладатися на два лінійних множники.

Щоб знайти рівняння цих прямих, потрібно розв’язати рівняння даної лінії як квадратне відносно однієї зі змінних х або у як невідомої величини, вважаючи другу змінну за відому величину.

Два розв’язки квадратного рівняння і дають два рівняння цих прямих. За знайденими рівняннями вони і можуть бути побудованими в початковій системі .

Мал.16

Значить, при переході до нових осей в даному випадку необхідності немає.

Приклад 3. Побудувати лінію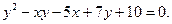

Розв’язок. 1. Обчислимо інваріанти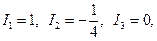

так як 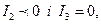то лінія буде складатися з двох прямих, що перетинаються.

2. Зведемо дане рівняння до вигляду:

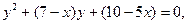
Розв’яжемо його відносно у:

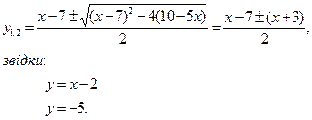
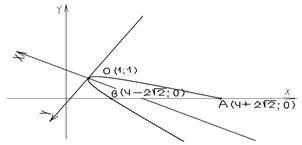
3. Побудуємо прямі за їх знайденими рівняннями (мал.17).

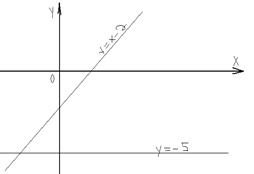
Вправи. Побудувати лінії: