Центр кривої другого порядку

Визначення. Центром лінії другого порядку називається така точка, відносно якої для будь-якої точки лінії знайдеться симетрична точка цієї лінії.

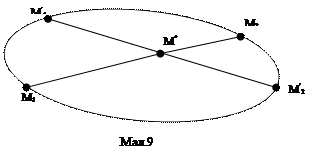
Нехай М^*(х^*, у^*) – центр лінії другого порядку. Якщо М₁(х₁, у₁) – будь-яка точка лінії другого порядку, то, виходячи з визначення центра, повинна існувати точка на цій лінії М₂(х₂, у₂) така, що 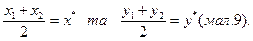(6)

Запишемо тепер рівняння прямої, яка проходить через точку М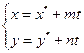^*: (7)

і поставимо умову, точка М₁ , а значить, і точка М₂ лежали на прямій (мал.9).

Тоді маємо:

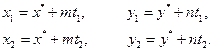
(де t₁,t₂ – значення параметра t, при яких із рівняння (7) можна отримати координати точок М₁ та М₂), звідки:

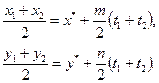(8)

Порівняємо рівності (8) та (6) і, враховуючи, що координати m та n направляючого вектора прямої не рівні нулю одночасно, ми приходимо до висновку, що t₁+t₂=0, а, значить, в рівнянні

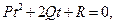
За теоремою Вієтта Q=0, тобто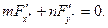

Не будемо розглядати той випадок, коли рівняння другого степеню буде парою співпавши прямих, тоді на будь-якій із ліній знайдеться в крайньому випадку дві пари точок М₁, М₂, і М^’₁, М^’₂, симетричних відносно М^*, через котрі пройдуть дві прямі з різними напрямками

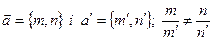
і, що значить,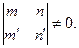

Умова Q=0 повинно мати місце для прямих з цими напрямками, тобто одночасно мають місце рівності: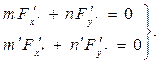

Так як у цій системі однорідних рівнянь з невідомими 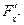та 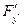визначник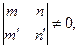

то вона повинна мати один визначений розв’язок (причому ненульовий)

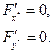
Або в розгорнутому вигляді:

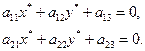(9)

Безпосередньо із визначення центра випливає, що у випадку, коли лінія другого порядку складається з пари співпадаючих прямих, то будь-яка її точка буде центром. Можна сказати, що координати будь-якої точки цієї лінії задовольняють рівнянням (9).

І навпаки, якщо для точки М^*(х^*, у^*) виконуються умови 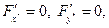то маємо:

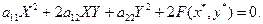
А таке рівняння разом з точкою М₁(X, Y) буде задовольняти і точка М₂(X, Y), симетрична точці М₁ відносно М^*, яка являється у даному випадку початком координат.

Таким чином, необхідна та достатня умова того, щоб точка М^* була центром, полягає в тому, щоб координати цієї точки задовольняли рівнянням (9).

Дослідимо рівняння цієї системи:

а) Якщо 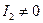, то система (9) має єдиний розв’язок, а з цього слідує, що лінія другого порядку має один визначений центр. До таких ліній відносяться: еліпс, гіпербола і дві прямі, що перетинаються; вони називаються центральними.

б) Якщо 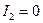, але хоча б один із визначників

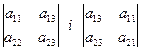
не дорівнює нулю, то система (9) не має розв’язків.

Прямі, що відповідають рівнянням (9), паралельні і, значить, перетинаються у нескінченності. Іноді зручно говорити, що у цьому випадку центром є нескінченно віддалена точка. До таких ліній відноситься парабола.

в) Якщо в рівняннях (9) не всі коефіцієнти одного із рівнянь нулі та:

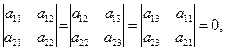
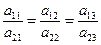тоді (11)

і одне з рівнянь системи (9) буде наслідком другого,

відповідні їм прямі співпадають, точка перетину їх,

тобто центр, стає невизначеною; всяка точка цих

співпавши прямих (9) буде центром.

У цьому випадку ми маємо пряму центрів.

Якщо в одному з рівнянь (9) всі коефіцієнти нулі,

як, наприклад, для лінії, яка задається рівнянням 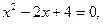тоді з двох рівнянь системи (9) залишається одне, і, значить, в цьому випадку ми маємо пряму центрів.

Очевидно, що в розглянутому випадку

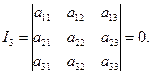
Відомо, що при умові І₂=0, І₃=0 лінія другого порядку буде складатися з двох паралельних чи співпадаючих прямих.

2. Діаметр лінії другого порядку.

Визначення. Діаметром лінії другого порядку називається геометричне місце середин паралельних хорд.

Нехай напрям паралельних хорд визначається вектором 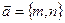(мал.10).

Якщо М(Х, Y) – середина однієї з цих хорд, тоді для рівняння 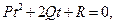яке визначає точки перетину хорди з лінією (1) 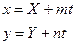, повинна виконуватися умова:

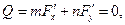
або в розгорнутому вигляді:

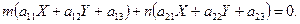(12)

Ця умова повинна виконуватися для усіх хорд даного напряму. При переході від однієї хорди до іншої X та Y будуть змінюватися і, значить, в умові (12) їх слід при цьому вважати змінними.

Рівняння (12) буде, таким чином, рівнянням діаметра. Так як рівняння (12) - рівняння першого степеня, то діаметром буде пряма лінія. Замінивши 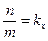(кутовий коефіцієнт хорд), ми можемо записати рівняння (12) у вигляді:

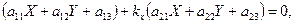(13)

або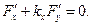

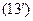
У випадку центральних ліній рівняння (13) перетворюється в тотожність при підстановці координат центру і, значить, діаметри проходять через центр.

Розв’язавши рівняння (13) відносно Y, знайдемо кутовий коефіцієнт діаметра

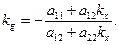(14)

Покажемо, що для ліній параболічного типу (парабола та паралельні прямі) k_g не залежить від k_x.

І справді, для ліній параболічного типу: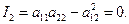

Визначивши звідси 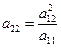та підставивши у рівність (14), маємо:

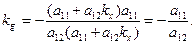
Таким чином, для ліній параболічного типу всі діаметри паралельні між собою та мають кутовий коефіцієнт: 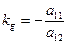(15)

асимптотичного напрямку (мал.11).

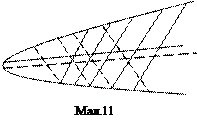Перетворивши рівність (14), маємо:

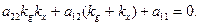
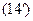
Ми бачимо, що в цій рівності k_g та k_x відіграють рівносильну роль, а це значить, що якщо ми візьмемо сукупність паралельних хорд з кутовим коефіцієнтом k_g, то діаметр, який є геометричним місцем їх середин, матиме кутовий коефіцієнт k_g.

Два діаметри, кожен з яких ділить хорди, паралельно другому, наполовину, називаються спряженими.

Рівність 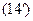буде умовою спряженості двох напрямів.

Якщо спряжені напрями перпендикулярні, то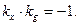

Підставляючи в рівність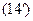

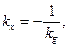
маємо: 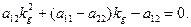(15)

Таким чином, для будь-якої кривої другого порядку існують два взаємно перпендикулярних спряжених напрями.

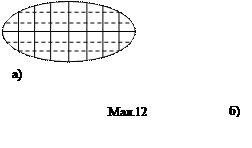
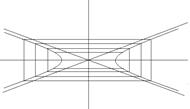
Взаємно перпендикулярні та спряжені діаметри еліпса та гіперболи являються осями симетрії. Вони називаються осями цих кривих: а) великою та малою – для еліпса, б) дійсною та уявною – для гіперболи (мал.12).

Мал.13

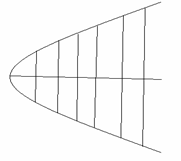Так як всі діаметри параболи паралельні, то вона має одну вісь симетрії – діаметр, перпендикулярний до спряжених до нього хорд (мал.13).

IV.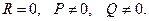

В цьому випадку рівняння (3) набирає вигляду:

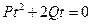і один із коренів t₁=0, це означає, що одна з точок перетину прямої та лінії другого порядку співпадає з даною точкою прямої –М₀.

Це ж слідує безпосередньо з рівності:

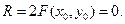
V.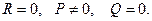

В цьому випадку рівняння набирає вигляду: Pt²=0.

Як наслідок, t₁=t₂=0 та обидві точки перетину прямої та лінії другого порядку зливаються з точкою М₀. Пряма буде дотичною до лінії другого порядку в точці М₀.

З умови

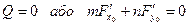
Визначимо кутовий коефіцієнт дотичної:

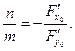
Знаючи точку дотику та кутовий коефіцієнт дотичної , можна записати рівняння дотичної:

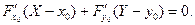(16)

VI.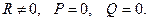

Аналогічно випадку ІІ, тут можна довести, що точки перетину прямої та лінії другого порядку співпадатимуть з нескінченно віддаленою точкою цієї лінії, і, як наслідок, пряма буде дотичною до лінії другого порядку в її нескінченно віддаленій точці.

Дотична до лінії другого порядку в її нескінченно віддаленій точці називається асимптотою.

Умова Q=0 визначає рівняння діаметру

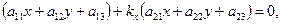
а умова Р=0, або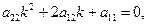

вказує, що наш діаметр спряжений з асимптотичним напрямком.

Таким чином, асимптота, яка визначається умовами Р=0 та Q=0, є діаметром, спряженим з асимптотичним напрямком.

Покажемо, що асимптотичний напрямок – це напрямок, який співпадає зі спряженим до нього. Спряжені напрями пов’язані формулою:

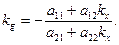
Поклавши 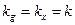, отримуємо:

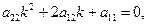
а цій рівності, як відомо, задовольняють асимптотичні напрями.

Таким чином, асимптота лінії другого порядку - це пряма, яка являє собою два спряжені діаметри.

Вище було з’ясовано, що лінії гіперболічного типу (I₂<0) мають два дійсних асимптотичних напрями і, значить, гіпербола має дві дійсні асимптоти (мал.14).

Еліпс (І₂>0) не має асимптотичних напрямів і, значить, еліпс не має асимптот.

Парабола (І₂=0) має один асимптотичний напрямок

Мал.14

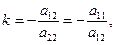
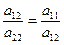який співпадає з напрямом діаметрів параболи (рівність слідує з умови І₂=0), і, значить, парабола має одну асимптоту, котра буде нескінченно віддаленою прямою, що дотикається параболи в її нескінченно віддаленій точці. (Суворе доведення цього може бути проведене в однорідних координатах і тому не приводиться).

VII.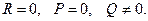

Цей випадок дає ті ж результати, що і випадок ІІ, але з тим доповненням, що дана точка М₀ прямої лежить на лінії другого порядку, що задається умовою

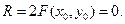
VIII.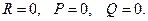
В цьому випадку рівняння (3) задовольняється будь-яким значенням параметра t, а, значить, вся точки прямої (2) належать лінії другого порядку (1), що можливо у тому випадку, коли лінія другого порядку розпадається на пару паралельних прямих або пару прямих, що перетинаються і пряма (2) співпадає із однією з них.

Приклад 1.

Знайти центр лінії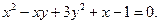

Розв’язок.

Прирівнюючи часткові похідні по x та по y лівої частини рівняння до нуля, отримаємо:

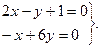
Розв’язавши ці рівняння, отримуємо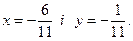

З цього слідує, що лінія має єдиний центр в точці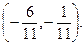

Приклад 2.

Знайти центр лінії: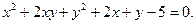

Розв’язок.

Рівняннями, що визначають центр, будуть:

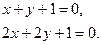
Ця система несумісна. Прямі, що відповідають цим рівнянням, паралельні. Це означає ,що лінія не має центру (центр – нескінченно віддалена точка).

Приклад 3.

Знайти центр лінії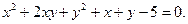

Розв’язок.

Рівняння, що визначають центр, задаються як:

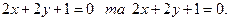
В цьому випадку лінія має нескінченну множину центрів, а точніше, всі точки прямої

.

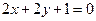Приклад 4.

Знайти середину хорди, яка відсікається кривою

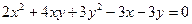
на прямій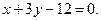

Розв’язок.

Через середину даної хорди повинен проходити спряжений їй діаметр. Складемо його рівняння.

Із рівняння хорди маємо: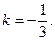

Рівняння діаметра має вид:

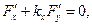
тобто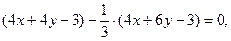

або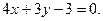

Розв’язуючи це рівняння сумісно з рівнянням хорди, визначаємо її середину:

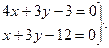
Розв’язок цієї системи буде таким:

х= - 3, у= 5.

Це значить, що серединою хорди буде точка (-3, 5).

Приклад 5.

Знайти вісі кривої:

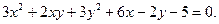
Розв’язок.

Вісі кривої – діаметри, спряжені та взаємно перпендикулярні. Кутові коефіцієнти їх визначаються з рівняння (16).

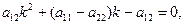
тобто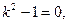

звідки k₁=1, k₂= -1.

Рівняння осей знаходяться як рівняння діаметрів, спряжених даним напрямам, тобто

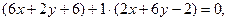
або

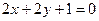
і

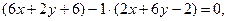
або

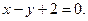
Приклад 6.

Знайти асимптоти гіперболи:

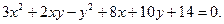
Розв’язок.

Рівняння асимптот має вигляд:

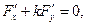
де k визначається з рівняння

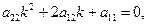
тобто

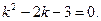
Розв’язавши його, матимемо:

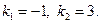
Складемо рівняння асимптот:

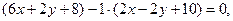
або

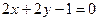
і

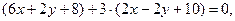
або

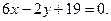
Приклад 7.

Скласти рівняння дотичної до еліпса 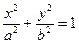в точці (х₀, у₀).

Розв’язання.

Рівняння дотичної до лінії, яка задана загальним рівнянням, має вигляд:

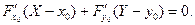
В нашому випадку

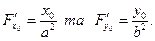
Значить рівняння дотичної матиме вигляд:

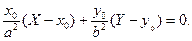
Перетворивши, маємо:

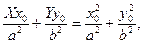
Так як точка (х₀, у₀) лежить на еліпсі, то права частина рівності буде дорівнювати 1, а рівняння дотичної матиме вигляд:

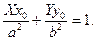
Вправи.

1. Написати рівняння дотичних до кривої 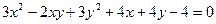в її точках з абсцисою -2.

Відповідь. 7х+4у+10=0,

3х-4у+18=0.

1. Через точку (1; -2) проведений діаметр кривої 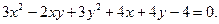Знайти рівняння цього діаметру та діаметру йому спряженого.

Відповідь. х+2у+3=0,

7х-5у+2=0.

1. Знайти головні осі кривої:

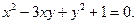
Відповідь. х+у=0,

х-у=0.

4. Знайти вісь симетрії та вершину параболи: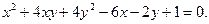

Відповідь. х+2у-1=0.

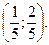
5. Якого виду набере рівняння кривої 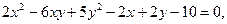якщо початок координат перемістити в її центр?

Відповідь.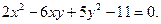

6. Знайти асимптоти гіперболи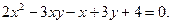

Відповідь. 2х-3у+1=0,

х-1=0.