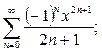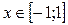II. Разложение в степенные ряды с использованием представления основных элементарных функций в виде ряда Маклорена
Имеют место разложения в ряды Маклорена следующих функций:
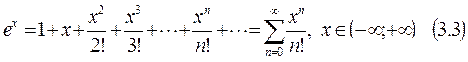
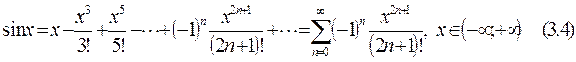
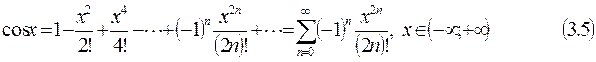
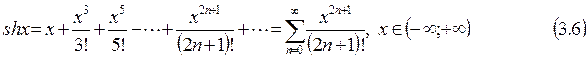
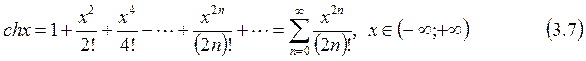
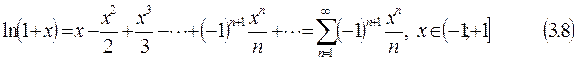
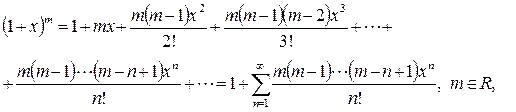
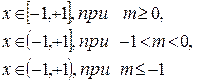(3.9)
Используя эти разложения, можно находить разложения других функций. При этом отпадает необходимость исследования поведения остаточного члена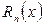 
, так как интервалы сходимости рядов, полученных для основных элементарных функций, известны.
Прежде чем приступить к дальнейшему рассмотрению, напомним некоторые свойства элементарных функций и формулы, их связывающие:
.
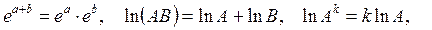
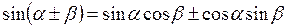
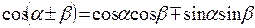
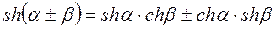
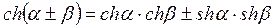
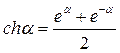
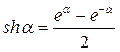Пример 3.3.Разложить функцию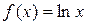 
в ряд Тейлора по степеням 
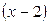. (Это второй способ решения примера 3.2.) Сведём задачу о
разложении в ряд Тейлора к разложению в ряд Маклорена, используя замену переменной.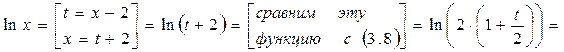 
.
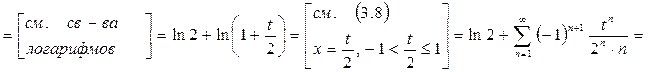
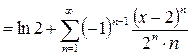Найдём область сходимости ряда к данной функции. Из разложения (3.8) имеем: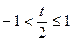 
.
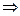
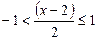
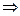
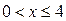Сравнивая результаты примеров 3.2 и 3.3, видим, что данный способ позволяет получить результат более рационально.
Пример 3.4. Разложить функцию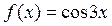 
по степеням 
.
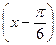Как и в предыдущем примере, сведём задачу о разложении в ряд Тейлора к разложению в ряд Маклорена с помощью линейной замены:
.
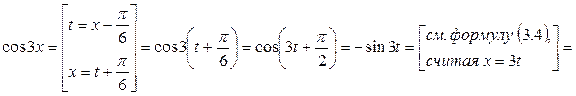
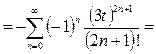
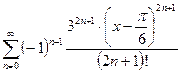Область сходимости полученного ряда: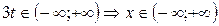 
.
Пример 3.5.Разложить функцию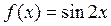 
по степеням 
.
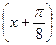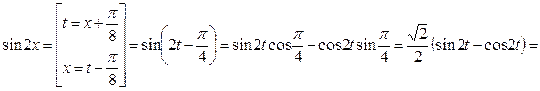
(Далее, с помощью формул (3.4) и (3.5), считая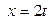 
, получаем):
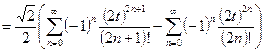
Заметим, что в полученном разложении присутствуют все степени 2t, начиная с нулевой. Попробуем объединить оба ряда в один вида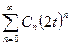 
:
.
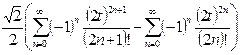
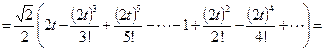
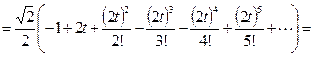
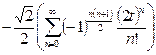Окончательно,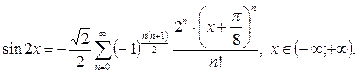 
P.S. Чередование знака по два в общем элементе можно записать следующим образом: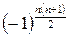 
, или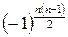 
.
Пример 3.6.Разложить функцию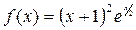 
по степеням 
.
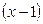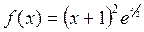
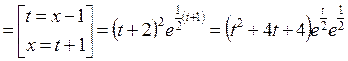
Далее, используя формулу (3.3), принимая в ней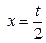 
, получаем:
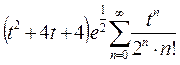
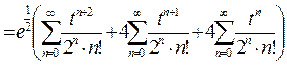. Получившиеся три ряда имеют одинаковые степени, начиная с 
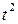. Преобразуем результат в одну сумму вида 
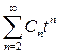. Сначала «сместим» индексы так, чтобы в каждой из сумм степени t были одинаковыми. Для этого в первой сумме заменим n+2 на n, во второй заменим n+1 на n. Суммы станут выглядеть так:
.
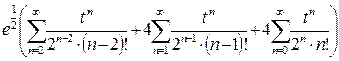У всех трёх сумм одинаковы степени t, начиная с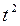 
.Вычислим слагаемые с меньшими степенями t, т.е. 
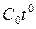и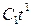 
.
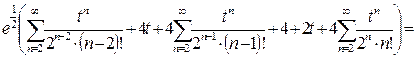
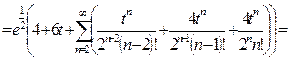
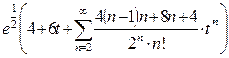
Ответ: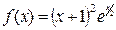 
.
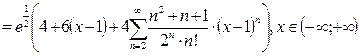Пример 3.7.Разложить функцию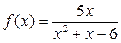 
по степеням 
.
.
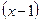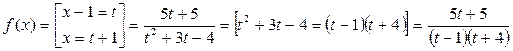Представим полученную дробь в виде суммы простых дробей методом неопределённых коэффициентов: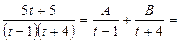 
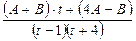
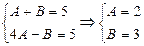. Итак, исходную функцию можно представить в виде: 
.
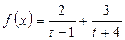Далее, с помощью (3.10),получим: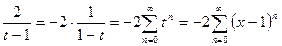 
.
Так как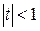 
, область сходимости этого ряда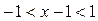 
.
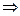
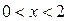Аналогично,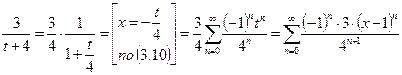 
.
Так как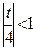 
, область сходимости этого ряда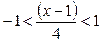 
.
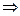
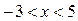Окончательно,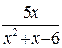 
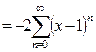
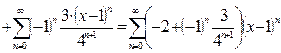
Область сходимости полученного ряда: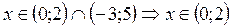 
.
Пример 3.8.Разложить функцию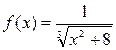 
по степеням x.
.
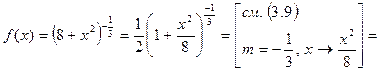
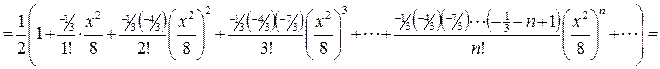
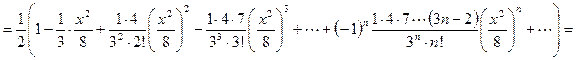
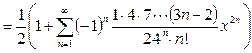Область сходимости данного ряда: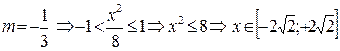 
.
Пример 3.9.Разложить функцию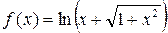 
в ряд Маклорена.
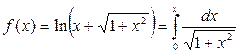. Напомним, что степенной ряд можно почленно интегрировать в области сходимости. Разложим с помощью формулы (3.9) для m=-1/2 в ряд Маклорена функцию 
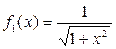,а затем, проинтегрировав полученный ряд, получим разложение исходной функции.
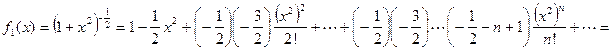
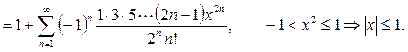
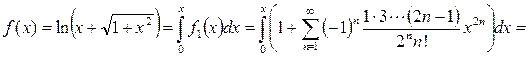
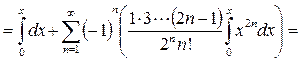
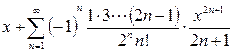. Область сходимости полученного ряда 
.
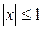Контрольное задание.
Разложить данные функции в ряды по степеням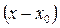 
и найти
области сходимости полученных рядов:
1. 
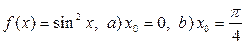; Ответ: a)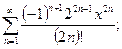 
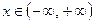b)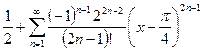 
, .
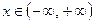2. 
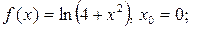Ответ: 
. 
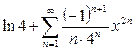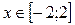
3. 
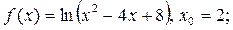Ответ: 
, 
.
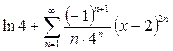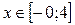4. 
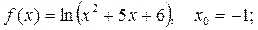Ответ: 
, 
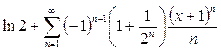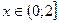
5. 
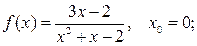Ответ: 
, 
.
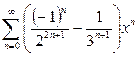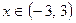6. 
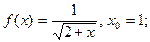Ответ: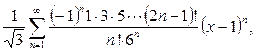 
.
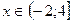7. 
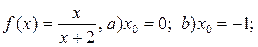Ответ: a)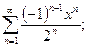 
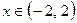, b)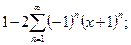 
.
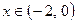8. Используя метод интегрирования степенного ряда, разложить в ряд Маклорена и указать область сходимости: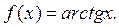 
Ответ: 
