Практические задачи на нахождение наибольшего и наименьшего значения функции
При решении таких задач вначале проводят их формализацию, т.е. записывают с помощью математических формул. Для этого в задаче выделяют величину, наибольшее или наименьшее значение которой нужно найти, и ту переменную (или переменные), от значений которой зависит искомая величина. Зависимость между величиной и переменной оформляют в виде функции. Если переменных несколько, то, используя условие задачи, их можно выразить через одну.
Следующий обязательный шаг, о котором, к сожалению, часто забывают, это установление реальных границ изменения переменной, исходя из условия задачи (т.е. нахождение области определения составленной функции). После формализации находят наибольшее или наименьшее значение рассматриваемой в задаче функции одним из способов, рассмотренных в предыдущем разделе.
Пример 1. Прямоугольный лист жести имеет линейные размеры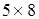 
(дм). В четырех его углах вырезают одинаковые квадраты и делают открытую коробку, загибая края под прямым углом. Какова наибольшая вместимость полученной коробки?
 |
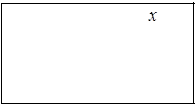Вместимость коробки определяется ее объемом, поэтому нужно найти размер стороны квадрата, при котором объем будет наибольшим. Обозначим сторону квадрата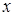 
. Тогда объем коробки:
.
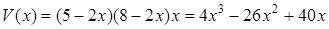Как следует из рисунка: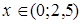 
. Исследуем 
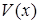на наличие экстремумов. 
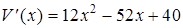. Из условия 
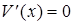получим уравнение: 
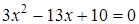, его корни: 
, 
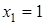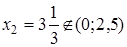. Определим знак производной 
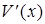на 
.
 |
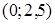Из рисунка видно, что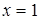 
точка единственного экстремума на области определения функции 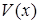, т.к. этот экстремум – максимум, значит, он будет наибольшим значением .
.
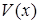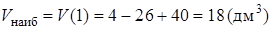Пример 2. Каковы должны быть размеры открытого сверху цилиндрического сосуда вместимостью V, чтобы на его изготовление пошло наименьшее количество материала?
Обозначим радиус основания цилиндра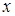 
, а высоту – 
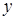. Тогда площадь поверхности открытого сверху цилиндрического сосуда, которая и определяет расход материала, равна: 
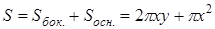. Поскольку объем сосуда задан, то имеющуюся функцию двух переменных, можем преобразовать в функцию одной переменной. Т.к. 
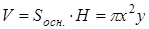, то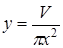 
, тогда
, 
.
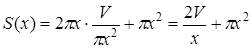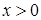Найдем производную:
.
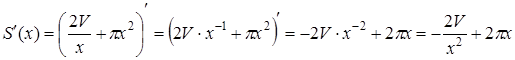Найдем критические точки производной, для этого приравняем ее нулю:
.
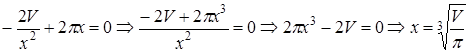Критическая точка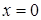 
, в которой производная не существует, не принадлежит области определения функции, поэтому ее в дальнейшем не рассматриваем.
Для установления вида экстремума найдем вторую производную и определим ее значение в критической точке.
; 
.
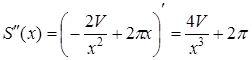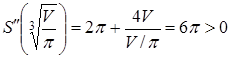Т.к. вторая производная положительна, то в рассматриваемой точке имеется минимум, поскольку это единственный экстремум на области задания функции, значит, в нем достигается наименьшее значение функции.
Т.о. наименьший расход материала будет при следующих размерах: радиус основания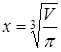 
, высота 
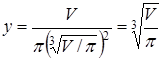, при этом площадь поверхности сосуда равна 
.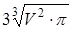