Формулы полной вероятности и Байеса

Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместимых событий B₁, B₂, ..., B_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

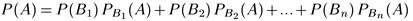(формула полной вероятности).

Для приема зачета преподаватель заготовил 50 задач: 20 задач по дифференциальному исчислению, 30 по интегральному исчислению. Для сдачи зачета студент должен решить первую же доставшуюся наугад задачу. Какова вероятность для студента сдать зачет, если он умеет решить 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению?

Решение. Вероятность получить задачу по дифференциальному исчислению (событие B₁) равна Р(B₁) = 0,4, по интегральному исчислению (событие В₂) — Р(В₂) = 0,6. Если событие А означает, что задача решена, то Р_B1(А) = 0,9, Р_В2(А) = 0,5. Теперь по формуле полной вероятности имеем:

Р(А) = 0,4·0,9 + 0,6·0,5 = 0,36 + 0,3 = 0,66.

Имеются три одинаковых по виду ящика. В первом находятся две белые мыши и одна серая, во втором — три белые и одна серая, в третьем — две белые и две серые мыши. Какова вероятность того, что из наугад выбранного ящика будет извлечена белая мышь?

Решение. Обозначим В₁ — выбор первого ящика, В₂ — выбор второго ящика, В₃ — выбор третьего ящика, А — извлечение белой мыши.

Так как все ящики одинаковы, то Р(В₁) = Р(B₂) = Р(В₃) = 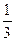. Если выбран первый ящик, то 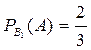. Аналогично , .

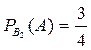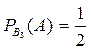Наконец, по формуле полной вероятности получаем:

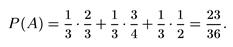
В санатории 30% пациентов – мужчины (М) и 70% – женщины (Ж). Сердечные болезни среди мужчин встречаются в два раза чаще, чем среди женщин. Какова вероятность, что наугад выбранный пациент сердечник?

Решение. Обозначив С – наличие сердечного заболевания, можно написать Р(М) = 0,3, Р(Ж) =0,7, Р_М(С) = 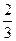, Р_Ж(С) = .

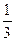Подставляя это в формулу полной вероятности G), получим

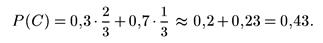
Формула Байеса применяется, когда событие A, которое может появиться только с одной из гипотез H₁, H₂ ,..., Н_n, произошло и необходимо произвести количественную переоценку априорных вероятностей этих гипотез Р(H₁), Р(H₂), ..., Р(H_n), известных до испытания, т.е. найти апостериорные (получаемые после проведения испытания) условные вероятности гипотез P(H₁/A), P(H₂/A),..., Р(H_n/А):

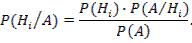
Или вместо Р(А) используем ее значение, вычисленное по формуле полной вероятности:

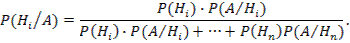
Итак, пусть до опыта имеются гипотезы H₁ ,H₂, ..., Н_n. После опыта становится известной информация о результатах опыта, но не полная, а именно: результаты наблюдений показывают, что наступило некоторое событие.

Считается, что до опыта были известны (априорные) вероятности гипотез Р(H₁),Р(H₂), ...,Р(Н_n) и условные вероятности P(A/H₁), P(A/H₂),..., Р(A/H_n). Необходимо определить апостериорные вероятности гипотез P(H₁/A), P(H₂/A),..., Р(H_n/А).

Значение формулы Байеса состоит в том, что при наступлении события А, т.е. по мере получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы. Такой подход называется байесовским.

Предположим, что в некоторой большой популяции мужчин и женщин поровну. В этой популяции 5% мужчин и 0,25% женщин страдают дальтонизмом. Случайным образом выбирают одного дальтоника. Какова вероятность того, что этот человек – мужчина?

Решение: Популяция разделена на два непересекающихся подмножества – мужчин и женщин. Мы ищем Р(М½Д). По теореме Байеса

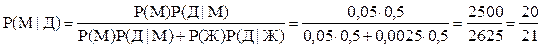
Установлено, что курящие мужчины в возрасте свыше 40 лет умирают от рака легких в 10 раз чаще, чем не курящие мужчины. Если предположить, что 60% мужчин курящие, то какова вероятность того, что мужчина, умерший от рака легких, был курящим?

Решение: Событие К – мужчина курит, P(К)=0,6.

Событие Р – мужчина умирает от рака легких.

Событие Н – мужчина не курит

Р(Н)=0,4.

Тогда

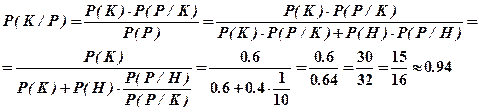
94% - курящих мужчин умирают от рака легких

6% - некурящих мужчин умирают от рака легких.

Пример 28. Предположим, что женщина с группой крови О и мужчина с группой крови АВ имеют двоих близнецов с группой крови В. Если известно, что примерно в 1/4 случаев рождения близнецов они происходят из одного яйца, то какова вероятность того, что однояйцевыми являются и упомянутые близнецы?

Решение. Множество мальчиков-близнецов разбивается на однояйцевых и двуяйцевых. По теореме Байеса искомую вероятность можно записать как

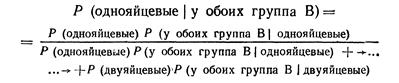
Чтобы вычислить эти условные вероятности, мы должны знать, что когда скрещиваются О и АВ, у 50% потомства окажется группа А и у 50% — группа В. Если близнецы происходят из одного яйца, то у них одна группа крови. Поскольку А и В равновероятны, Р (у обоих группа В | однояйцевые) = 1/2. Если бы они развивались из двух разных яиц, то у каждого была бы группа В с вероятностью 1/2. Поэтому Р (у обоих группа В| двуяйцевые) = 1/4. Следовательно,

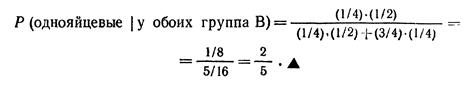
12.9. Варианты заданий

№ 12.1. В коробке находится лабораторная мышь, которая с равной вероятностью может быть либо черной, либо белой. В коробку добавляется белая мышь, затем наугад извлекается мышь, оказавшаяся белой. Какова вероятность того, что оставшаяся мышь является белой?

№ 12.2. Предположим, что 5% всех мужчин и 0,25 % всех женщин - дальтоники. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это женщина? (Считать, что мужчин и женщин одинаковое число).

№ 12.3. Имеется две одинаковых клетки с крысами. В первой клетке 2 белых и 1 черная крыса, а во второй – 1 белая и 4 черных. Наудачу выбирают одну клетку и вынимают из нее крысу для опыта. Какова вероятность того, что оставшаяся крыса является белой?

№ 12.4. Два автомата производят одинаковые хирургические зажимы. Производительность первого автомата вдвое больше, чем второго. Первый автомат производит в среднем 60% зажимов отличного качества, а второй - 84%. Наудачу взятый зажим оказался отличного качества. Найти вероятность того, что он произведен первым автоматом.

№ 12.5. В пяти аптечках находятся одинаковые по массе и размерам таблетки. В двух - по 6 зеленых и 4 желтых таблеток. (Это аптечка состава H₁). В двух других аптечках (состава Н₂) – по 8 зеленых и 2 желтых таблеток. В одной аптечке (состава H₃) – 2 зеленых и 8 желтых таблеток. Наудачу выбирается аптечка и из нее извлекается таблетка, которая оказалась зеленой. Какова вероятность того, что зеленая таблетка извлечена из аптечки первого состава?

№ 11.9.6. Лабораторное животное либо здорово (с вероятностью 0,9), либо нет. Если животное здорово, то оно может выполнить некоторое задание в 75% всех попыток. Если животное нездорово, то оно способно выполнить это задание лишь в 40% всех попыток. Допустим, что предпринимается попытка и животное не справляется с заданием. Какова вероятность того, что животное здорово?

№ 12.7. Одна вакцина формирует иммунитет против краснухи в 95% случаев. Предположим, что вакцинировалось 30% популяции. Предположим также, что вероятность заболеть краснухой у вакцинированного человека без иммунитета такая же, как и у невакцинированного. Какова вероятность того, что человек, заболевший краснухой, был вакцинирован?

№ 12.8. Некоторое заболевание, встречающееся у 5% населения, с трудом поддается диагностике. Один грубый тест на это заболевание дает положительный результат (указывающий на наличие заболевания) в 60% случаев, когда пациент действительно болен, и в 30% случаев, когда у пациента нет этого заболевания. Пусть для конкретного пациента этот тест дает положительный результат. Какова вероятность, что у него есть это заболевание?

№ 12.9. В некоторой большой популяции число черноволосых и рыжих одинаково. Замечено, что у 30% людей с черными волосами глаза голубые, так же как и у 50% людей с рыжими волосами. Из тех, у кого черные или рыжие волосы, случайно выбирают одного человека и оказывается, что у него голубые глаза. Какова вероятность того, что у этого человека черные волосы?

№ 12.10. На одном производстве было установлено, что 3% рабочих являются алкоголиками с показателем прогулов втрое выше, чем у остальных рабочих. Если случайно выбранный рабочий отсутствует на работе, то какова вероятность того, что он алкоголик?

№ 12.11. В эксперименте живой амебе пересаживают ядро от одной, цитоплазму от второй и внешнюю оболочку от третьей амебы. Если все компоненты берут из одного и того же штамма, то около 85% воспроизводятся нормально. Если компоненты берут из различных штаммов амебы, то нормально воспроизводится лишь 1%. Допустим, что из одного и того же штамма и из разных штаммов было собрано одинаковое число амеб. Если выбирают наудачу одну из этих амеб и она воспроизводится нормально, то какова вероятность того, что ее компоненты брались из одного штамма?

№ 12.12. Лабораторная крыса обучается выполнению четырех заданий за ограниченное время в 5 мин каждое. Когда задание выполняется в пределах отведенного времени, нажатие крысой на рычаг приводит к получению порции пищи. Вероятности успешного выполнения заданий за отведенное время соответственно составляют 0,8; 0,6; 0,4; 0,2. Предположим, что крыса начинает выполнять случайно выбранное задание и через 5 мин обнаруживается, что она получила пищу. Какова вероятность того, что крыса выполнила первое задание? второе задание?

№ 12.13. Экспериментальные мыши содержатся в двух клетках. В первой клетке содержится 5 коричневых и 6 белых мышей, а во второй – 2 коричневые и 5 белых. Случайным образом выбирают клетку и на нее наугад извлекают одну мышь. Если эта мышь коричневая, то какова вероятность того, что она извлечена из второй клетки?

№ 12.14. Для проверки контагиозности нескольких штаммов бактерий большое число морских свинок содержалось парами в отдельных клетках. По одной из каждой пары свинок заражалось штаммом I, II или III (по каждому штамму бралось равное количество морских свинок). Установлено, что доли здоровых свинок, заразившихся от своих соседей, равны 1/3, 1/4 и 3/4. В выбранной наугад клетке обе свинки оказываются зараженными. Каковы вероятности того, что заражение вызвано штаммами I, II и III?

№ 12.15. В одной большой частной лечебнице согласно оценкам 50% мужчин и 30% женщин имеют серьезные нарушения сердечной деятельности. В этой лечебнице женщин вдвое больше, чем мужчин. У случайно выбранного пациента оказалось серьезное нарушение сердечной деятельности. Какова вероятность, что этот пациент — мужчина?

№ 12.16. Большая популяция разбита на две группы одинаковой численности. Одна группа придерживалась специальной диеты с высоким содержанием ненасыщенных жиров, а контрольная группа питалась по обычной диете, богатой насыщенными жирами. После 10 лет пребывания на этих диетах возникновение сердечно-сосудистых заболеваний составляло в этих группах соответственно 31 и 48%, Случайно выбранный из популяции человек имеет сердечно-сосудистое заболевание. Какова вероятность того, что этот человек принадлежит контрольной группе?

№ 11.9.17. Краснуха может оказаться причиной серьезных врожденных пороков развития у детей, если мать заболевает ею на ранних стадиях беременности. Вероятность пороков оценивается как 45, 20 и 5%, если заболевание происходит соответственно на первом, втором и третьем месяцах беременности. Предположим, что вероятность заболеть краснухой одна и та же на любом месяце беременности и что ребенок рождается с серьезными пороками по причине краснухи. Какова вероятность того, что мать заболела краснухой на первом месяце беременности?

№ 12.18. Установлено, что курящие мужчины в возрасте свыше 40 лет умирают от рака легких в 10 раз чаще, чем некурящие мужчины. В предположении, что 65% этой популяции курящие, какова вероятность того, что мужчина, умерший от рака легких, был не курящим?

№ 12.19. а) Вероятность того, что американский лось переносит зиму, оценивается в 80%, если лось здоров, и в 30%, если лось болен. Если в популяции больны 20% лосей, то какая доля популяции перенесет зиму?

б) Если волки убивают 80% здоровых и 70% больных лосей из тех, что не выживают за зиму, то какую долю убитые волками за зиму лоси составляют во всей популяции?

№ 12.20. Редкое заболевание встречается у 0,1% населения и с трудом поддается диагностике. Один грубый тест на это заболевание дает положительный результат (указывающий на наличие заболевания) в 75% случаев, когда у пациента это заболевание есть, и в 25% случаев, когда его нет. Допустим, что тест дает положительный результат, для случайно выбранного человека. Тогда тест проводят вторично и получают отрицательный результат. В предположении, что результаты теста независимы, какова вероятность, что у этого человека имеется заболевание?

№ 12.21. Установлено, что в среднем один из 700 детей мужского пола рождается с лишней Y-хромосомой и что у таких детей крайне агрессивное поведение встречается в 20 раз чаще. Опираясь на эти данные, представьте, что у мальчика крайне агрессивное поведение. Какова вероятность того, что ребенок имеет лишнюю Y-хромосому?

№ 12.22. Из 20 студентов. пришедших на экзамен, 8 подготовлены отлично, 6 - хорошо, 4 - посредственно и 2 - плохо. В экзаменационных билетах имеется 40 вопросов. Студент, подготовленный отлично, знает все вопросы, хорошо - 35. посредственно - 25 и плохо - 10 вопросов. Некоторый студент ответил на все 3 вопроса билета, Найдите вероятность того, что он подготовлен: а) хорошо; б) плохо.

№ 12.23. Одна вакцина формирует иммунитет против краснухи в 95% случаев. Предположим, что вакцинировалось 30% населения. Предположим также, что вероятность заболеть краснухой у вакцинированного человека без иммунитета такая же, как и у не вакцинированного. Какова вероятность того, что человек, заболевший краснухой вакцинирован?

№ 12.24. На город примерно 100 дней в году дует ветер с севера и 200 дней в году — с запада. Промышленные предприятия, расположенные на севере, производят выброс вредных веществ каждый третий день, а расположенные на западе — в последний день каждой недели. Как часто город подвергается воздействию вредных выбросов? Иными словами, какова вероятность того, что в наугад выбранный день город будет накрыт промышленным смогом?

№ 12.25. Бросается монета, и если она падает так, что сверху оказывается герб, вынимаем один шар из урны 1; в противном случае - из урны 2. Урна 1 содержит 3 красных и 1 белый шар. Урна 2 содержит 1 красный и 3 белых шара. а) Какова вероятность того, что вынутый шар красный? б) Какова вероятность того, что шар вынимался из первой урны, если он оказался красным?