Первая космическая скорость

02.12.2014

Урок 22 (10 класс)

Тема. Искусственные спутники Земли. Развитие космонавтики.

О движении бросаемых тел

В 1638 г. в Лейдене вышла книга Галилея «Беседы и математические доказательства, касающиеся двух новых отраслей науки». Четвертая глава этой книги называлась «О движении бросаемых тел». Не без труда удалось ему убедить людей в том, что в безвоздушном пространстве «крупинка свинца должна падать с такой же быстротой, как пушечное ядро». Но когда Галилей поведал миру о том, что ядро, вылетевшее из пушки в горизонтальном направлении, находится в полете столько же времени, что и ядро, просто выпавшее из ее жерла на землю, ему не поверили. Между тем это действительно так: тело, брошенное с некоторой высоты в горизонтальном направлении, движется до земли в течение такого же времени, как если бы оно просто упало с той же высоты вертикально вниз.
Чтобы убедиться в этом, воспользуемся прибором, принцип действия которого иллюстрирует рисунок 104, а. После удара молоточком М по упругой пластине П шарики начинают падать и, несмотря на различие в траекториях, одновременно достигают земли. На рисунке 104, б изображена стробоскопическая фотография падающих шариков. Для получения этой фотографии опыт проводили в темноте, а шарики через равные интервалы времени освещали яркой вспышкой света. При этом затвор фотоаппарата был открыт до тех пор, пока шарики не упали на землю. Мы видим, что в одни и те же моменты времени, когда происходили вспышки света, оба шарика находились на одной и той же высоте и столь же одновременно они достигли земли.

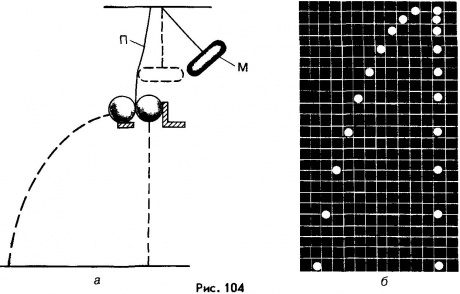
Время свободного падения с высоты h (вблизи поверхности Земли) может быть найдено по известной из механики формуле s=аt2/2. Заменяя здесь s на h и а на g, перепишем эту формулу в виде

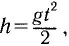
откуда после несложных преобразований получим

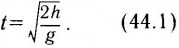
Такое же время будет находиться в полете и тело, брошенное с той же высоты в горизонтальном направлении. В этом случае, согласно Галилею, «к равномерному беспрепятственному движению присоединяется другое, вызываемое силой тяжести, благодаря чему возникает сложное движение, слагающееся из равномерного горизонтального и естественно ускоренного движений».
За время, определяемое выражением (44.1), двигаясь в горизонтальном направлении со скоростью v0 (т. е. с той скоростью, с которой оно было брошено), тело переместится по горизонтали на расстояние

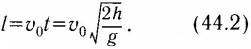
Из этой формулы следует, что дальность полета тела, брошенного в горизонтальном направлении, пропорциональна начальной скорости тела и возрастает с увеличением высоты бросания.
Чтобы выяснить, по какой траектории движется в этом случае тело, обратимся к опыту. Присоединим к водопроводному крану резиновую трубку, снабженную наконечником, и направим струю воды в горизонтальном направлении. Частицы воды при этом будут двигаться точно так же, как и брошенное в том же направлении тело. Отворачивая или, наоборот, заворачивая кран, можно изменить начальную скорость струи и тем самым дальность полета частиц воды (рис. 105), однако во всех случаях струя воды будет иметь форму параболы. Чтобы убедиться в этом, позади струи следует поставить экран с заранее начерченными на нем параболами. Струя воды будет точно соответствовать изображенным на экране линиям.

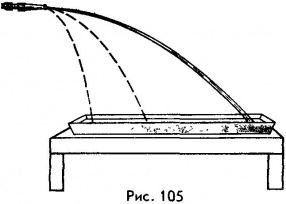
Итак, свободно падающее тело, начальная скорость которого горизонтальна, движется по параболической траектории.
По параболе будет двигаться тело и в том случае, когда оно брошено под некоторым острым углом к горизонту. Дальность полета в этом случае будет зависеть не только от начальной скорости, но и от угла, под которым она была направлена. Проводя опыты со струей воды, можно установить, что наибольшая дальность полета при этом достигается тогда, когда начальная скорость составляет с горизонтом угол 45° (рис. 106).

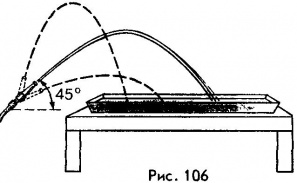
При больших скоростях движения тел следует учитывать сопротивление воздуха. Поэтому дальность полета пуль и снарядов в реальных условиях оказывается не такой, как это вытекает из формул, справедливых для движения в безвоздушном пространстве. Так, например, при начальной скорости пули 870 м/с и угле 45° в отсутствие сопротивления воздуха дальность полета составила бы примерно 77 км, между тем как в действительности она не превышает 3,5 км.

Первая космическая скорость

Вычислим скорость, которую надо сообщить искусственному спутнику Земли, чтобы он двигался по круговой орбите на высоте h над Землей.
На больших высотах воздух сильно разрежен и оказывает незначительное сопротивление движущимся в нем телам. Поэтому можно считать, что на спутник действует только гравитационная сила 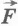, направленная к центру Земли (рис.4.4).

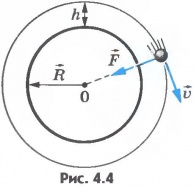
По второму закону Ньютона .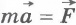
Центростремительное ускорение спутника определяется формулой 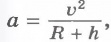, где h - высота спутника над поверхностью Земли. Сила же, действующая на спутник, согласно закону всемирного тяготения определяется формулой 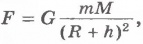, где M - масса Земли.
Подставив значения F и a в уравнение для второго закона Ньютона, получим

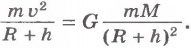
Отсюда

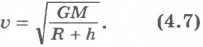
Из полученной формулы следует, что скорость спутника зависит от его расстояния от поверхности Земли: чем больше это расстояние, тем с меньшей скоростью он будет двигаться по круговой орбите. Примечательно то, что эта скорость не зависит от массы спутника. Значит, спутником Земли может стать любое тело, если ему сообщить определенную скорость. В частности, при h=2000 км=2•10⁶ м скорость v≈6900 м/с.
Минимальная скорость, которую надо сообщить телу на поверхности Земли, чтобы оно стало спутником Земли, движущимся по круговой орбите, называется первой космической скоростью.
Первую космическую скорость 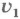можно найти по формуле (4.7), если принять h=0:

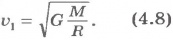
Подставив в формулу (4.8) значение G и значения величин M и R для Земли, можно вычислить первую космическую скорость для спутника Земли:

Если такую скорость сообщить телу в горизонтальном направлении у поверхности Земли, то при отсутствии атмосферы оно станет искусственным спутником Земли, обращающимся вокруг нее по круговой орбите.
Такую скорость спутникам способны сообщать только достаточно мощные космические ракеты. В настоящее время вокруг Земли обращаются тысячи искусственных спутников.
Любое тело может стать искусственным спутником другого тела (планеты), если сообщить ему необходимую скорость.

Движение искусственных спутников

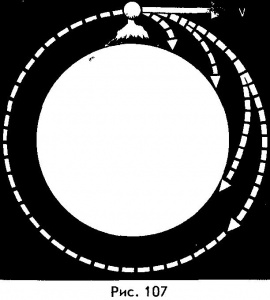
В работах Ньютона можно найти замечательный рисунок, показывающий, как можно осуществить переход от простого падения тела по параболе к орбитальному движению тела вокруг Земли (рис. 107). «Брошенный на землю камень,- писал Ньютон,- отклонится под действием тяжести от прямолинейного пути и, описав кривую траекторию, упадет наконец на Землю. Если его бросить с большей скоростью, то он упадет дальше». Продолжая эти рассуждения, нетрудно прийти к выводу, что если бросить камень с высокой горы с достаточно большой скоростью, то его траектория могла бы стать такой, что он вообще никогда не упал бы на Землю, превратившись в ее искусственный спутник.

Минимальная скорость, которую необходимо сообщить телу у поверхности Земли, чтобы превратить его в искусственный спутник, называется первой космической скоростью.
Для запуска искусственных спутников применяют ракеты, поднимающие спутник на заданную высоту и сообщающие ему в горизонтальном направлении требуемую скорость. После этого спутник отделяется от ракеты-носителя и продолжает дальнейшее движение лишь под действием гравитационного поля Земли. (Влиянием Луны, Солнца и других планет мы здесь пренебрегаем.) Ускорение, сообщаемое этим полем спутнику, есть ускорение свободного падения g. С другой стороны, поскольку спутник движется по круговой орбите, это ускорение является центростремительным и поэтому равно отношению квадрата скорости спутника к радиусу его орбиты. Таким образом,

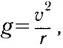
Откуда

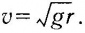
Подставляя сюда выражение (43.1), получаем

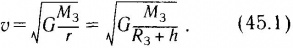
Мы получили формулу круговой скорости спутника, т. е. такой скорости, которую имеет спутник, двигаясь по круговой орбите радиусомr на высоте h от поверхности Земли.
Чтобы найти первую космическую скорость v1, следует учесть, что она определяется как скорость спутника вблизи поверхности Земли, т. е. когда h<<R3 и r≈R3. Учитывая это в формуле (45.1), получаем

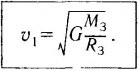
Подстановка в эту формулу числовых данных приводит к следующему результату:

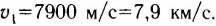
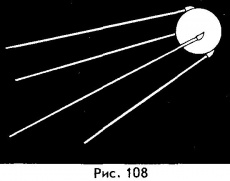
Сообщить телу такую огромную скорость впервые удалось лишь в 1957 г., когда в СССР под руководством С. П. Королева был запущен первый в мире искусственный спутник Земли (сокращенно ИСЗ). Запуск этого спутника (рис. 108) - результат выдающихся достижений в области ракетной техники, электроники, автоматического управления, вычислительной техники и небесной механики.

В 1958 г. на орбиту был выведен первый американский спутник «Эксплорер-1», а несколько позже, в 60-х гг., запуски ИСЗ произвели и другие страны: Франция, Австралия, Япония, КНР, Великобритания и др., причем многие спутники были запущены с помощью американских ракет-носителей.
В настоящее время запуск искусственных спутников является привычным делом, и в практике космических исследований уже давно получило широкое распространение международное сотрудничество.
Запускаемые в разных странах спутники могут быть разделены по своему назначению на два класса:
1. Научно-исследовательские спутники. Они предназначены для изучения Земли как планеты, ее верхней атмосферы, околоземного космического пространства, Солнца, звезд и межзвездной среды.
2. Прикладные спутники. Они служат удовлетворению земных нужд народного хозяйства. Сюда относятся спутники связи, спутники для изучения природных ресурсов Земли, метеорологические спутники, навигационные, военные и др.
К ИСЗ, предназначенным для полета людей, относятся пилотируемые корабли-спутники и орбитальные станции.
Помимо работающих спутников на околоземных орбитах обращаются вокруг Земли и так называемые вспомогательные объекты: последние ступени ракет-носителей, головные обтекатели и некоторые другие детали, отделяемые от ИСЗ при выводе их на орбиты.
Заметим, что из-за огромного сопротивления воздуха вблизи поверхности Земли спутник не может быть запущен слишком низко. Например, на высоте 160 км он способен совершить всего лишь один оборот, после чего снижается и сгорает в плотных слоях атмосферы. По этой причине первый искусственный спутник Земли, выведенный на орбиту на высоте 228 км, просуществовал только три месяца.
С увеличением высоты сопротивление атмосферы уменьшается и при h>300 км становится пренебрежимо малым.
Возникает вопрос: а что будет, если запустить спутник со скоростью, большей первой космической? Расчеты показывают, что если превышение незначительно, то тело при этом остается искусственным спутником Земли, но движется уже не по круговой, а по эллиптической орбите. С увеличением скорости орбита спутника становится все более вытянутой, пока наконец не «разрывается», превратившись в незамкнутую (параболическую) траекторию (рис. 109).

Минимальная скорость, которую нужно сообщить телу у поверхности Земли, чтобы оно ее покинуло, двигаясь по незамкнутой траектории, называется второй космической скоростью.
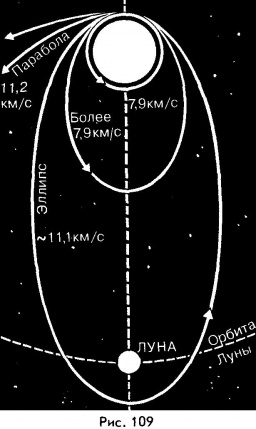
Вторая космическая скорость в √2 раза больше первой космической:

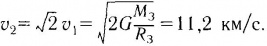
При такой скорости тело покидает область земного притяжения и становится спутником Солнца.
Чтобы преодолеть притяжение Солнца и покинуть Солнечную систему, нужно развить еще большую скорость - третью космическую. Третья космическая скорость равна 16,7 км/с. Имея примерно такую скорость, автоматическая межпланетная станция «Пионер-10» (США) в 1983 г. впервые в истории человечества вышла за пределы Солнечной системы и сейчас летит по направлению к звезде Барнарда.

Примеры решения задач

Задача 1. Тело бросают вертикально вверх со скоростью 25 м/с. Определите высоту подъема и время полета.

Дано: Решение:

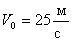
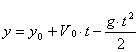; 0=0+25^.t-5^.t²

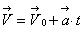; 0=25-10^.t₁; t₁=2,5c; Н=0+25^.2,5-5^.2,5²=31,25 (м)

t- ? 5t=25; t=5c

H - ? Ответ: t=5c; Н=31,25 (м)

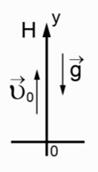
Рис. 1. Выбор системы отсчета

Сначала мы должны выбрать систему отсчета. Систему отсчета выбираем связанную с землей, начальная точка движения обозначена 0. Вертикально вверх направлена ось Оу. Скорость 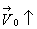направлена вверх и совпадает по направлению с осью Оу. Ускорение свободного падения направлено вниз 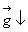по той же оси.

Запишем закон движения тела. Нельзя забывать о том, что скорость и ускорение величины векторные.

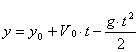
Следующий шаг. Обратите внимание, что конечная координата, в конце, когда тело поднялось на некоторую высоту, а потом упало обратно на землю, будет равна 0. Начальная координата также равна 0: 0=0+25^.t-5^.t².

Если решить это уравнение, получим время: 5t=25; t=5 c.

Определим теперь максимальную высоту подъема. Сначала определим время подъема тела до верхней точки. Для этого мы используем уравнение скорости: .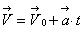

Мы записали уравнение в общем виде: 0=25-10^.t₁,t₁=2,5 c.

Когда мы подставляем известные нам значения, то получаем, что время подъема тела, время t₁ составляет 2,5 с.

Здесь бы хотелось отметить то, что все время полета составляет 5 с, а время подъема до максимальной точки 2,5 с. Это означает, что тело поднимается ровно столько времени, сколько потом будет обратно падать на землю. Теперь воспользуемся уравнением, которое мы уже использовали, – закон движения. В этом случае мы вместо конечной координаты ставим Н, т.е. максимальную высоту подъема: Н=0+25^.2,5-5^.2,5²=31,25 (м).

Произведя несложные расчеты, получаем, что максимальная высота подъема тела составит 31,25 м. Ответ: t=5c; Н=31,25 (м).

В данном случае мы воспользовались практически всеми уравнениями, которые изучали при исследовании свободного падения.

Задача 2. Определите высоту над уровнем Земли, на которойускорение свободного падения уменьшается в два раза.

Дано: Решение:

R_З =6400 км ; ;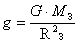

.

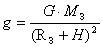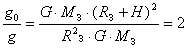
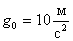
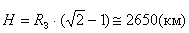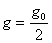
Н -? Ответ: Н ≈ 2650 км.

Для решения этой задачи нам потребуется, пожалуй, одно единственное данное. Это радиус Земли. Он равен 6400 км.

Ускорение свободного падения определяется на поверхности Земли следующим выражением: 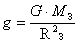. Это на поверхности Земли. Но стоит нам только удалиться от Земли на большое расстояние, ускорение будет определяться уже следующим образом: .

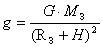Если теперь мы разделим эти величины друг на друга, получим следующее: .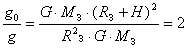

Сокращаются постоянные величины, т.е. гравитационная постоянная и масса Земли, а остается радиус Земли и высота, и это отношение равно 2.

Преобразуя теперь полученные уравнения, находим высоту: .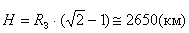

Если подставить значения в полученную формулу, получаем ответ: Н ≈ 2650 км.

Задача 3.Тело движется по дуге радиусом 20 см со скоростью 10 м/с. Определите центростремительное ускорение.

Дано: СИ Решение:

R=20 см 0,2 м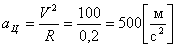

V=10 м/с

а_Ц - ? Ответ: а_Ц = .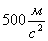

Формула для вычисления центростремительного ускорения известна. Подставляя сюда значения, мы получаем: 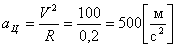. В этом случае центростремительное ускорение получается огромным, посмотрите на его значение 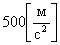. Ответ: а_Ц = .

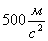После решения этой, казалось бы, несложной задачи, хотелось бы отметить следующее. Посмотрите еще раз на значение ускорения, заметьте, что тело движется по дуге всего лишь радиусом 20 см и скорость-то невелика (всего 10 м/с), а какое получается огромное ускорение. Можете себе представить, какие огромные ускорения и перегрузки возникают в движущемся колесе автомобиля. Там ведь скорость довольно большая, бывает, гораздо больше 10 м/с.

Задача 4.Определите высоту над уровнем Земли, на которойускорение свободного падения уменьшается в два раза.

Дано: Решение:

R_З =6400 км ; ;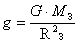

.

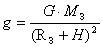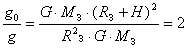
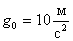
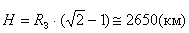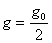
Н -? Ответ: Н ≈ 2650 км.

Для решения этой задачи нам потребуется, пожалуй, одно единственное данное. Это радиус Земли. Он равен 6400 км.

Ускорение свободного падения определяется на поверхности Земли следующим выражением: 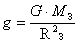. Это на поверхности Земли. Но стоит нам только удалиться от Земли на большое расстояние, ускорение будет определяться уже следующим образом: .

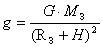Если теперь мы разделим эти величины друг на друга, получим следующее: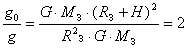

Сокращаются постоянные величины, т.е. гравитационная постоянная и масса Земли, а остается радиус Земли и высота, и это отношение равно 2.

Преобразуя теперь полученные уравнения, находим высоту: .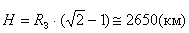

Если подставить значения в полученную формулу, получаем ответ: Н ≈ 2650 км.

Домашнее задание

1. Е.В. Коршак, А.И. Ляшенко, В.Ф. Савченко. Физика. 10 класс, «Генеза», 2010. Читать с.83-84.

2. Законспектировать лекцию.

3. Ответить на вопросы:

- От чего зависит дальность полета тела, брошенного в горизонтальном направлении? По какой траектории движется такое тело?

- Под каким углом к горизонту следует бросать с земли мяч, чтобы дальность его полета оказалась максимальной?
- Как влияет сопротивление воздуха на движение брошенных тел?
- По какой траектории движется тело, брошенное с самолета, относительно: а) Земли; б) самолета?

- Какую скорость называют первой космической?
- Как изменяется скорость движения спутника по орбите с увеличением высоты h?
- Зависит ли скорость движения спутника от его массы?
- Как направлены скорость и ускорение спутника, движущегося по круговой орбите? Чему равно ускорение такого спутника?
- Можно ли считать круговое движение спутника равноускоренным? Почему?
- На какие два класса делят искусственные спутники Земли?
- Какую скорость называют второй космической? Чему она равна?
- Что представляет собой третья космическая скорость?