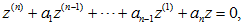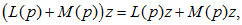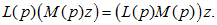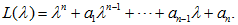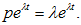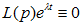Теорема о структуре общего решения линейного однородного дифференциального уравнения

Если y₁, y₂,… y_n есть линейно независимые решения линейного однородного дифференциального уравнения, то

y = c₁ y₁ + c₂ y₂ + … + c_n y_n

есть общее решение этого уравнения.

18. ЛОДУ n-го порядка. Свойства решений ЛОДУ n-го порядка. Теорема об общем решении ЛОДУ n-го порядка.

19. ЛОДУ n-го порядка с постоянными коэффициентами.

Уравнение n-го порядка для одной неизвестной функции z независимого переменного t с постоянными коэффициентами имеет вид:

(2.1)

где a₁,¼,a_n - постоянные числа (действительные или комплексные). К уравнению (2.1), очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось. (См. соответствующую формулировку в первом параграфе первой главы). Решения уравнения (2.1) будут построены в явном виде и тем самым установлена еще раз теорема существования. Теорема единственности будет использоваться по существу для доказательства того, что найдены все решения данного уравнения.

Данное выражение в соответствии с равенством (2.5) представляет собой линейную операцию над функцией z, т.е.

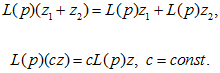(2.7)

С другой стороны само выражение (2.6) представляет собой выражение относительно символа p с постоянными (действительными или комплексными) коэффициентами, для которого справедливы обычные алгебраические правила оперирования, т.е. если L(p) и M(p) - два произвольных многочлена относительно символа p (или, как говорят, оператора дифференцирования p), то

Предложение 2.1.1 Если L(p) -многочлен относительно оператора дифференцирования вида (2.6), то справедлива следующая формула

(2.8)

Здесь l - произвольное действительное или комплексное число;

Доказательство. Мы имеем

Отсюда следует, что 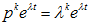и поэтому справедлива формула (2.8).

Из формулы (2.8) следует, что функция e^lt является решением уравнения (2.1), т.е.

тогда и только тогда, когда число l есть корень многочлена L(l), т.е.

L(l) = 0.

(2.9)

Многочлен L(l) называется характеристическим многочленом уравнения (2.1), а уравнение (2.9) - характеристическим уравнением.

Совокупность всех решений уравнений (2.1) описывается несколько по разному в зависимости от того имеет ли кратные корни характеристическое уравнение (2.9), либо корни простые. Рассмотрим отдельно эти случаи.

20. ЛНДУ n-го порядка. Метод вариации произвольных постоянных.

Дифференциальное уравнение n-го порядка называется линейным, если оно первой степени относительно совокупности искомой функции у и ее производных у', ..., y⁽ⁿ⁾, т. е. имеет вид

y⁽ⁿ⁾ + a₁(x) y^(n-1) + … + a_n(x) y = 0, (1)

где а₀(x), а₂(x), ..., а_n(x) - заданные функции от х или постоянные, причем а₀(x) ≠ 0 для всех значений х из той области, в которой мы рассматриваем уравнение

21. ЛНДУ со специальной правой частью.

22. Числовые ряды. Необходимый признак сходимости ряда. Достаточный признак расходимости ряда.

23. Признаки сравнения положительных рядов.

24. Признаки сходимости положительных рядов.

25. Знакопеременные ряды. Знакочередующиеся ряды. Признак Лейбница.

Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда являетсязнакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.