Свойства общего решения дифференциального уравнения
Раздел 8. Дифференциальные уравнения
Общая характеристика дифференциальных уравнений
Определение обыкновенного дифференциального уравнения
И дифференциального уравнения в частных производных
Решение различных геометрических, физических и экономических задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту или иную задачу, с некоторой функцией этих переменных и производными этой функции различных порядков.
В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.
Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:
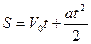 .
.
В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S, т.е.
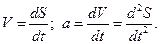
Тогда получаем: 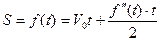 - уравнение связывающее функцию
- уравнение связывающее функцию 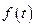 с независимой переменной t и производной второго порядка функции
с независимой переменной t и производной второго порядка функции 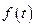 .
.
Определение. Дифференциальным уравнениемназывается уравнение, связывающее независимые переменные, неизвестные функции и производные различных порядков от неизвестных функций по независимым переменным.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Пример. 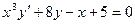 - обыкновенное дифференциальное уравнение 1 – го порядка. Общий вид:
- обыкновенное дифференциальное уравнение 1 – го порядка. Общий вид: 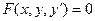 .
.
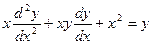 - обыкновенное дифференциальное уравнение 2 – го порядка. Общий вид:
- обыкновенное дифференциальное уравнение 2 – го порядка. Общий вид: 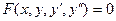
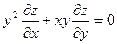 - дифференциальное уравнение в частных производных первого порядка.
- дифференциальное уравнение в частных производных первого порядка.
Определение. Общим решениемдифференциального уравнения называется дифференцируемая функция одного или нескольких аргументов, которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.
В дальнейшее будем рассматривать дифференциальные уравнения, содержащие неизвестную функцию одного независимого аргумента.
Свойства общего решения дифференциального уравнения
1) Любое дифференциальное уравнение имеет бесконечное множество решений. 2) При задании начальных условий 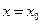 ,
, 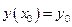 существует такое значение
существует такое значение 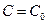 , при котором решением дифференциального уравнения является функция
, при котором решением дифференциального уравнения является функция 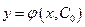 .
.
Определение. Решение вида 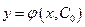 называется частным решениемдифференциального уравнения.
называется частным решениемдифференциального уравнения.
Определение. Задачей Кошиназывается нахождение любого частного решения дифференциального уравнения вида 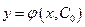 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 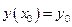 .
.
Теорема Коши (о существовании и единственности решения дифференциального уравнения 1- го порядка) Если функция 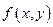 непрерывна в некоторой области D в плоскости
непрерывна в некоторой области D в плоскости 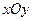 и имеет в этой области непрерывную частную производную
и имеет в этой области непрерывную частную производную 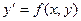 , то какова бы не была точка
, то какова бы не была точка 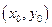 в области D, существует единственное решение
в области D, существует единственное решение 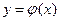 уравнения
уравнения 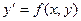 , определенное в некотором интервале, содержащем точку
, определенное в некотором интервале, содержащем точку 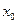 и принимающее при
и принимающее при 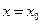 значение
значение 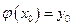 , т.е. существует единственное решение дифференциального уравнения.
, т.е. существует единственное решение дифференциального уравнения.
Определение. Интеграломдифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.
Пример. Найти общее решение дифференциального уравнения 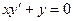 .
.
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
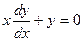 ;
; 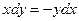 ;
; 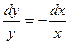 /
/
Интегрируем:
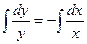 ;
;
и находим:
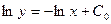 ;
; 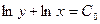 ;
; 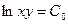 ;
; 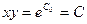 ;
; 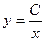 -
-
общее решение исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: 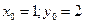 , тогда
, тогда
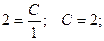
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
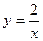
Определение. Интегральной кривойназывается график 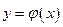 решения дифференциального уравнения на плоскости
решения дифференциального уравнения на плоскости 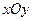 .
.
Определение. Особым решениемдифференциального уравнения называется такое решение, во всех точках которого условие единственности решения задачи Коши не выполняется, т.е. в окрестности некоторой точки 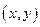 существует не менее двух интегральных кривых.
существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Пример. Найти общее решение дифференциального уравнения: 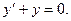 Найти особое решение, если оно существует. Имеем
Найти особое решение, если оно существует. Имеем
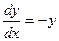 ;
; 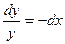 ;
; 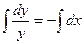 ;
; 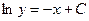 ;
; 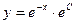 ;
; 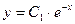 .
.
Данное дифференциальное уравнение имеет также особое решение 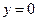 .
.
Далее рассмотрим подробнее приемы и методы, которые используются при решении дифференциальных уравнений различных типов.
