Виды симметрии периодических негармонических сигналов. Спектр негармонического периодического процесса

ЭЛЕКТРИЧЕСКИХ

ЦЕПЕЙ

Экзамен

II курс (2 семестр)

Содержание

1. Понятие о колебаниях негармонической формы. Математическая модель негармонического периодического процесса, выраженная тригонометрическим рядом Фурье. 4

2. Виды симметрии периодических негармонических сигналов. Спектр негармонического периодического процесса. 5

3. Максимальное, действующее и среднее за период значения напряжений (токов) при негармоническом воздействии. Коэффициенты амплитуды и искажений. 7

4. Цепи R, L, C при негармоническом воздействии. Составление уравнения тока данных электрических цепей при негармоническом напряжении на входе. 9

5. Методика расчёта электрических цепей при негармоническом воздействии (на примере) 11

6. Соединение обмоток генератора и сопротивлений нагрузки звездой. Схема соединения, фазные и линейные токи и напряжения, соотношение между ними. Расчёт трёхфазной электрической цепи при соединении приёмника звездой. Мощность трёхфазной цепи при симметричной нагрузке. Роль нейтрального провода 13

7. Соединение обмоток генератора и сопротивлений нагрузки треугольником. Схема соединения, фазные и линейные токи и напряжения, соотношение между ними. Расчёт трёхфазной электрической цепи при соединении приёмника треугольником. Мощность трёхфазной цепи при симметричной нагрузке. 15

8. Идеальный и реальный колебательные контура. Основные характеристики колебательного контура (свободные колебания, частота и период свободных колебаний, характеристическое сопротивление, добротность) 17

9. Принципиальная схема последовательного колебательного контура. Резонанс напряжений в последовательном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе напряжений. Резонансная частота, добротность. Настройка колебательного контура в резонанс. 19

10. Расстройка колебательного контура. Виды расстроек. Входные АЧХ и ФЧХ последовательного колебательного контура. Характер реактивного сопротивления последовательного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной. 21

11. Передаточные АЧХ и ФЧХ последовательного колебательного контура, его избирательные свойства. Полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы.. 23

12. Принципиальная схема параллельного колебательного контура. Резонанс токов в параллельном колебательном контуре, условие резонанса. Свойства электрической цепи при резонансе токов. Резонансная частота, добротность. 26

13. Подключение параллельного колебательного контура к источникам напряжения и тока. Избирательность параллельного колебательного контура. 28

14. Входные АЧХ и ФЧХ параллельного колебательного контура. Характер реактивного сопротивления параллельного колебательного контура на резонансной частоте и на частотах больше и меньше резонансной 30

15. Передаточные АЧХ параллельного колебательного контура. Эквивалентная добротность, полоса пропускания. Прохождение через колебательный контур сигналов негармонической формы.. 32

16. Виды параллельных колебательных контуров. Контуры с неполным включением.. 33

Дополнение. Сравнение последовательного и параллельного контуров. 34

17. Электронные аналоги колебательных контуров. Электронный колебательный контур, его избирательные свойства. Достоинства электронного колебательного контура по сравнению с пассивными колебательными контурами. Гиратор. 35

18. Реактивные двухполюсники. Определение. Одно-, двух-, трехэлементные реактивные двухполюсники. Построение характеристик, χ = F(ω), φ = F(ω). Нулевые и полюсные частоты.. 37

19. Понятие о связанных системах. Виды связи. Коэффициент связи. 41

20. Связанные контура. Преобразование двухконтурной схемы одноконтурной схемой замещения. Входное сопротивление. 43

21. Вносимые сопротивления, их формулы. Влияние вторичного контура на процессы в первичном. Физический смысл вносимых сопротивлений. 45

22. Резонансы в связанных колебательных системах. Первый и второй частные резонансы.. 46

23. Полный и сложный резонансы в связанных колебательных системах. Слабая, сильная и критическая связь 48

24. Передаточные характеристики связанных колебательных систем. Полоса пропускания при изменении степени связи между контурами. 49

25. Переходные процессы в линейных электрических цепях. Причины возникновения и сущность переходных процессов. Коммутация. Законы коммутации. Классический метод расчёта переходных процессов. Свободная и принужденная составляющие. Определение постоянных интегрирования. 50

26. Анализ процессов при включении последовательной RL-цепи на постоянное напряжение классическим методом.. 51

27. Анализ процессов при коротком замыкании последовательной RL-цепи классическим методом.. 53

28. Анализ процессов заряда конденсатора классическим методом.. 54

29. Анализ процессов разряда конденсатора классическим методом.. 56

30. Операторный метод расчета. Основные положения операторного метода. Схемные функции к операторной форме. Расчёт цепи операторным методом на примере. 57

31. Единичная и импульсная функции. Переходная и импульсная характеристики цепи. 59

32. Переходные процессы в цепях 2-го порядка. Переходные процессы в последовательной RLC цепи при её включении на постоянное и синусоидальное напряжение. 60

33. Понятие о четырёхполюсниках. Классификация четырехполюсников. Эквивалентные схемы четырёхполюсников. Уравнение пассивного четырехполюсника в A-параметрах и h-параметрах. 63

34. Характеристическое сопротивление четырехполюсника. Расчет характеристического сопротивления методом холостого хода и короткого замыкания. Согласованный четырехполюсник. 65

35. Нагрузочный режим работы четырехполюсника. Рабочее затухание четырехполюсника в логарифмических единицах. Каскадное соединение четырехполюсников. 67

36. Дифференцирующие цепи. Область применения. Принципиальные электрические схемы. Анализ работы цепи при воздействии сигналов различной формы. Активные дифференцирующие цепи. 69

37. Интегрирующие цепи. Область применения. Принципиальные электрические схемы. Анализ работы цепи при воздействии сигналов различной формы. Активные интегрирующие цепи. 72

38. Понятие об электрических фильтрах, их классификация. Определения полосы пропускания и полосы задерживания фильтров. 75

39. Фильтры нижних частот Баттерворта. Электрическая схема фильтра, прохождение токов различных частот, характеристика рабочего затухания. Порядок расчета фильтра. 77

40. Фильтры верхних частот Баттерворта. Электрическая схема фильтра, прохождение токов различных частот, характеристика рабочего затухания. Порядок расчета фильтра. 79

41. Полосовые фильтры Баттерворта. Электрическая схема фильтра, прохождение токов различных частот, характеристика рабочего затухания. Порядок расчета фильтра. 80

42. Режекторные фильтры Баттерворта. Электрическая схема фильтра, прохождение токов различных частот, характеристика рабочего затухания. 82

43. Полиномиальные фильтры Чебышева. Электрические схемы, характеристики рабочего затухания ФНЧ, ФВЧ, ПФ Чебышева, неравномерность затухания в полосе пропускания. Расчет полосового фильтра Чебышева на конкретном примере. 83

44. Электрические схемы фильтров Золотарева. Характеристики рабочего затухания ФНЧ, ФВЧ, ПФ Золотарева. Физический смысл работы фильтров. 86

45. Активные фильтры. Особенности, принципиальные электрические схемы фильтров нижних и верхних частот. Понятие о расчете параметров фильтров. 89

46. Активные фильтры. Особенности, принципиальные электрические схемы полосовых фильтров. Линии задержки. 90

47. Синтез электрических цепей. Задача синтеза электрических цепей. Неоднозначность решения задач синтеза и проблема выбора решения. Методы синтеза пассивного двухполюсника. 92

1. Понятие о колебаниях негармонической формы. Математическая модель негармонического периодического процесса, выраженная тригонометрическим рядом Фурье

Несинусоидальные токи

Синусоида не несёт информации. Любую информацию несёт сигнал несинусоидальной формы. Получить несинусоидальные сигналы можно:

1. если есть источник несинусоидальных колебаний;

2. если есть несколько источников синусоидальных колебаний разных частот, включённых последовательно;

3. если синусоидальный сигнал подать на нелинейный элемент.

Возьмём два тока:

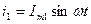
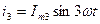
Сложим эти токи на временной диаграмме:

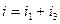
Выводы:

При сложении двух синусоид разных частот получается периодическая, но несинусоидальная функция. Справедливо и обратное.

Любую периодическую, но не синусоидальную функцию можно представить в виде суммы синусоид кратных частот. Такое представление называется разложение функции в ряд Фурье.

Синусоиды, входящие в ряд Фурье, называются гармоники.

Гармоника, частота которой совпадает с частотой несинусоидальной функции, называется первой или основной.

Гармоники, частоты которых в целое число раз больше частоты основной гармоники, называются высшими.

Гармоника, частота которой равна 0, называется постоянной составляющей или нулевой гармоникой.

Две формы ряда Фурье

1. Ряд Фурье с начальными фазами

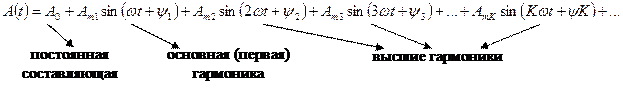
Раскрыв 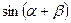получим ряд Фурье без начальных фаз:

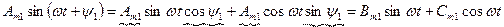
2. Ряд Фурье без начальных фаз

Виды симметрии периодических негармонических сигналов. Спектр негармонического периодического процесса

Виды симметрии

Если кривая имеет симметрию, то при разложении в ряд Фурье могут отсутствовать некоторые гармоники:

1. кривая симметрична относительно оси 0x

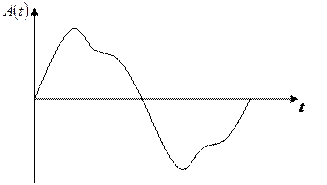
Такой симметрией обладает кривая тока в катушке с ферромагнитным сердечником.

При разложении в ряд Фурье присутствуют только нечётные синусоиды с начальными фазами:

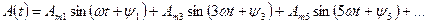
1. кривая симметрична относительно оси 0y

Такой симметрией обладает кривая тока на выходе одно- и двухполупериодного выпрямителя.

При разложении в ряд Фурье содержит постоянную составляющую и косинусоиды всех частот.

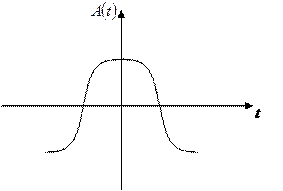
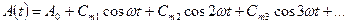
1. кривая симметрична относительно начала координат

При разложении содержит синусоиды всех частот без начальных фаз.

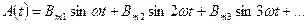
Спектр

Любой сигнал можно выразить временной и спектральной характеристикой.

Спектр — зависимость составляющих ряда Фурье от частоты. Чтобы его построить надо по оси 0x отложить частоту, а по оси 0y — амплитуду гармоник.

Пример:

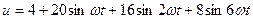
Масштаб:

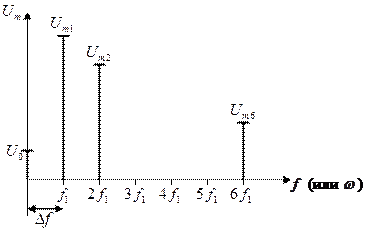
Спектр изображается спектральными линиями.

Расстояние между спектральными линиями 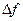— частота первой гармоники :

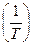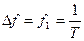
Вывод: спектр периодического сигнала дискретный или линейчатый. Изображается спектральными линиями.

Если 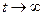, импульс становится одиночным, .

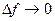Вывод: спектр непериодического сигнала сплошной.