Линейные дифференциальные уравнения

ГЛАВА V. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Основные понятия и определения

Определение 1. Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию у = у(х) и ее производные у', у'',…, у⁽ⁿ⁾, т.е. уравнение вида

F(х; у; у'; у'';…; у⁽ⁿ⁾) = 0.

Дифференциальное уравнение называется обыкновенным, если искомая функция у = у(х)есть функция одной независимой переменной х.

Определение 2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в него.

Определение 3. Решением дифференциального уравнения n-го порядка на интервале (а; b) называется функция у = j(х), определенная на интервале (а; b) вместе со своими производными до n-го порядка включительно, которая будучи подставлена в дифференциальное уравнение обращает его в тождество, т.е.

F(x; j(х); j'(х);…; j⁽ⁿ⁾(х)) º 0.

Обыкновенные дифференциальные уравнения

Первого порядка. Основные понятия

Определение 1.Дифференциальным уравнением первого порядка называется уравнение вида:

F(x; у; у') = 0. (4.1)

Если уравнение (4.1) удается разрешить относительно у', то получится

у' = f(x; у) (4.2)

- уравнение первого порядка, разрешенное относительно производной.

Иногда дифференциальные уравнения первого порядка записывают в дифференциалах

j(х; у) dх + g(x; у) dу = 0.

Определение 2. Общим решением дифференциального уравнения первого порядка называется функция у = j(х; C), зависящая от одной производной постоянной C и удовлетворяющая данному дифференциальному уравнению при любых допустимых значениях C.

Соотношение вида Ф(х; у; С) = 0, неявно определяющее общее решение, называется общим интегралом дифференциального уравнения первого порядка.

Определение 3. Частным решением дифференциального уравнения первого порядка называется решение, полученное из общего решения при каком-либо определенном значении постоянной С = С₀, т.е. у = j(х; С₀).

Соотношение, получаемое из общего интеграла при конкретном значении постоянной С, называется частным интегралом дифференциального уравнения.

С геометрической точки зрения совокупность всех решений дифференциального уравнения представляет собой совокупность кривых, называемых интегральными кривыми, а каждое частное решение представляет отдельную интегральную кривую.

Определение 4. Задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям, называется задачей Коши.

Задачей Коши в случае дифференциального уравнения первого порядка называют задачу нахождения решения у = у(х) уравнения у' = f(x; y), удовлетворяющего начальному условию у(х₀) = у₀ ( 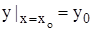), где х₀, у₀ - заданные числа.

Дифференциальные уравнения с разделяющимися

Переменными

Определение 1. Уравнение вида j(у) dу = g(x) dx называется дифференциальным уравнением с разделенными переменными.

Решение этого уравнения находится путем интегрирования обеих его частей. В результате чего его общий интеграл представляется в виде

F(y) = G(x) + C.

Определение 2. Уравнение вида у' = j(у) g(x)называется дифференциальным уравнением с разделяющимися переменными.

Решение дифференциального уравнения с разделяющимися переменными находится с помощью следующего алгоритма.

1. Заменить производную у' отношением дифференциалов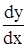

.

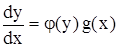2. Умножить обе части уравнения на dх

dу = j(у) g(x) dх.

3. Разделить переменные, т. е. распределить их так, чтобы функция, зависящая от у, располагалась при дифференциале dу, а функция, зависящая от х, при дифференциале dх.

Для этого последнее уравнение необходимо разделить на j(у). Получим 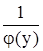dу = g(x) dх – уравнение с разделенными переменными.

4. Проинтегрировать обе его части ;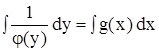

F(у) = G(x) + C – общий интеграл дифференциального уравнения.

5. Найти частный интеграл (решение), если задано начальное условие у(х₀) = у₀.

F(y) = G(x) + C₀.

Пример 1. Решить дифференциальное уравнение х у у' + 1 + х²= 0, если у(1) = 1.

Решение. Данное уравнение является дифференциальным уравнением с разделяющимися переменными. Решим его, используя предложенный алгоритм.

1. х у 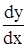+ 1 + х²= 0 ½ × dх.

2. х у dу + (1 + х²) dх = 0.

3. Разделим переменные, для чего разделим уравнение на х (х ¹ 0)

у dy = - .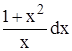

4. Проинтегрируем обе части уравнения

,

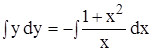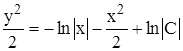*, С ¹ 0.

Преобразуя это выражение, получим общий интеграл в виде

x = С .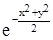

5. Найдем частный интеграл, используя начальное условие

у = 1 при х =1.

1 = С e^-1, C = e.

Откуда х = .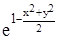

Линейные дифференциальные уравнения

Первого порядка

Определение 1. Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной. Оно имеет вид

у' + Р(х)у = Q(x), (4.3)

где Р(х) и Q(x) – заданные функции переменной х.

Если Q(x) º 0, то уравнение (4.3) называется линейным однородным. Оно является уравнением с разделяющимися переменными и имеет общее решение

у = .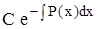

Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной (метод Лагранжа), который состоит в том, что решение уравнения (4.3) записывается в виде

у = ,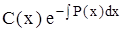

где С(х) – новая неизвестная функция от х.

Пример 1. Решить дифференциальное уравнение

у' + 2ху = 2х .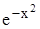

Решение. Применим метод вариации произвольной постоянной. Рассмотрим однородное уравнение у' + 2ху = 0, соответствующее данному неоднородному. Это уравнение с разделяющимися переменными. Найдем его общее решение, используя алгоритм, рассмотренный в §3.

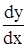+ 2ху = 0 ½ × dх

dу + 2 х у dх = 0.

Разделим переменные, поделив последнее уравнение на у

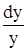+ 2х dх = 0.

В результате почленного интегрирования получим:

;

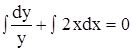ln|у| + х²+ ln|С₁| = 0, или ln|уС₁| = -х².

После потенцирования имеем у = С , .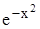

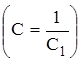Общее решение неоднородного уравнения ищем в виде

у = С(х) ,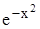

где С(х) – неизвестная функция переменной х.

Подставим данное выражение для у в исходное неоднородное дифференциальное уравнение.

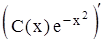+ 2х С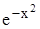(х) = 2 х .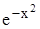

После дифференцирования и несложных преобразований получим дифференциальное уравнение относительно неизвестной функции С(х):

.

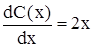Откуда после интегрирования имеем С(х) = х²+ C.

Итак, общее решение неоднородного уравнения будет

у = (х²+ C) ,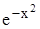

где C– постоянная интегрирования.

Существует другой метод (метод Бернулли) решения дифференциального уравнения (4.3), согласно которому нахождение общего решения уравнения (4.3) сводится к решению двух дифференциальных уравнений с разделяющимися переменными с помощью подстановки

у = u v, (4.4)

где u и v – неизвестные функции от х.

Дифференцируя (4.4), находим

у' = 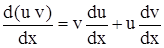.(4.5)

Подставив значения у и у' в уравнение (4.3), получим

,

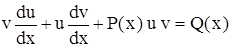или 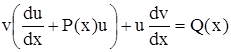. (4.6)

Так как искомая функция у подстановкой (4.4) представлена в виде произведения двух функций u и v, то одну из них, например u, мы можем выбрать по нашему усмотрению, кроме u = 0. Выберем u так, чтобы

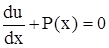. (4.7)

Решая это уравнение как уравнение с разделяющимися переменными, найдем функцию u = u(x). Найденную функцию подставим в уравнение (4.6).

U(x) 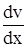= Q(x).(4.8)

Это уравнение с разделяющимися переменными, решая которое находим функцию v = v(x; C), содержащую произвольную постоянную C и являющуюся общим решением уравнения (4.8). Заменив в равенстве у = u v функции u и v найденными значениями, получим общее решение исходного дифференциального уравнения

у = u(x) v(x; C).

Частное решение находим, используя начальные условия.

Пример 2. Найти частное решение дифференциального уравнения

х (х – 1) у' + у = х²(2х – 1), у(2) = 4.

Решение. Данное уравнение является линейным дифференциальным уравнением первого порядка. Действительно, в результате деления обеих его частей на x (х – 1) (х ¹ 0; х ¹ 1) оно преобразуется к виду уравнения (4.3).

у' + 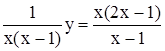. (4.9)

Найдем общее решение преобразованного дифференциального уравнения с помощью подстановки у = u v. При этом у' = u' v + u v'.

Подставляя у и у' в уравнение (4.9), будет иметь

u' v + u v' + ,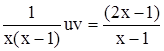

или

v 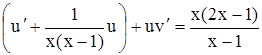. (4.10)

Выберем u так, чтобы выражение в скобках обратилось в нуль, т. е.

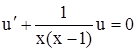. (4.11)

Тогда уравнение (4.10) примет вид

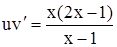. (4.12)

Решаем уравнение (4.11) как дифференциальное уравнение с разделяющимися переменными:

,

.

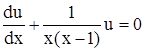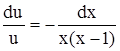Раскладывая дроби в правой части последнего уравнения 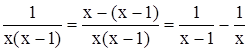, после интегрирования получим одно из его частных решений

,

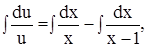
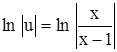или 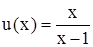. (4.13)

Подставив найденную функцию u(x) в уравнение (4.12), придем к дифференциальному уравнению относительно функции v.

,

,

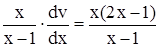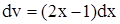интегрируя которое, получим

v(x; C) = х²– х + C. (4.14)

Заменив в подстановке у = u v функции u и v их выражениями из равенств (4.13) и (4.14), получим искомое общее решение данного дифференциального уравнения

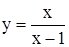(х²– х + С).

Найдем частное решение, удовлетворяющее начальному условию у = 4 при х = 2.

4 = 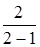(4 - 2 + С), т. е. С = 0.

Следовательно, искомым частным решением является функция

у = х².

* В данном случае, не нарушая общности, постоянную интегрирования C удобно представить в виде ln|C|.