Сжатие со случайными эксцентриситетами.

Характеризуется условием

e₀ ≤ e_a, (2.47)

где

e_a ≤ 10 мм; e_a ≤ h/30; e_a ≤ l/600; (2.48)

Расчет сжатых элементов из бетонов В15-В35 на действие продольной силы, приложенной со случайными эксцентриситетами e_a ≤ h/30 и при l₀ < 20h допускается производить из условия

N ≤φ(R_bА + R_scA´_s), (2.62)

где

φ= φ_b + 2(φ_sb – φ_b) α_s, причем φ ≤ φ_sb. (2.63)

φ_b и φ_sb – табличные коэффициенты, определяемые по данным таблиц.

N- расчетная продольная сила.

α_s = R_sA_s,tot / R_bA. (2.64)

Здесь A_s,tot площадь всей арматуры в сечении, площадь сечения бетона.

При α_s > 0,5 можно, не пользуясь формулой (2.63), принимать φ = φ_sb.

6.2. Сжатие с расчетными эксцентриситетами e₀ > e_a.

Влияние прогибов можно оценить без учета смещений от горизонтальных нагрузок и температурных или осадочных смещений путем умножения момента от вертикальных нагрузок на коэффициент η_v. Расчет допускается производить по недеформируемой схеме, а влияние прогиба оценивать коэффициентом η_v, определяемым по формуле

η_v = 1/(1- N / N_cr), (2.49)

где

N – расчетное усилие,

N_cr – условная критическая сила, определяемая по формуле

N_cr = π²D / l₀²,(2.50)

Расчет прочности сечений с симметричной арматурой производится в зависимости от относительной величины продольной силы N.

α_n = N / R_bbh₀. (2.55)

При α_n ≤ξ_R необходимое количество арматуры определяется по формуле

(2.56)

При α_n >ξ_R

(2.57)

Здесь

ξ – относительная высота сжатой зоны, определяемая по формуле

ξ = [α_n(1-ξ_R)+ 2α_s·ξ_R] / (1- ξ_R + 2 α_s), (2.58)

где

, (2.59)

ξ_l = (α_n + ξ_R) / 2 ≤ 1,0. (2.60)

(2.61)

Пример 6.1.

Рис. 6.1. Армирование сжатого элемента к примеру 6.1. 1 – 2Ø16 А400 АS= 4,02 см2, 2 – 4Ø8 А240 АS1 = 2,01 см2.

1 - 1

Определить площадь арматуры в сечении сжатого элемента. Продольная сила действует на колонну со случайными эксцентриситетами, сечение - прямоугольное с размерами b× h = 40×40 см. Бетон класса В20, R_b= 11,5 МПа, (11, 5·10³ кН/м²), рабочая арматура класса А400, R_s = R_sс = 355 МПа, (355·10³ кН/м² ). Расчетная продольная сила N =1800кН; длительно действующая часть N_l = 900кН; эксцентриситет приложения силы е₀ = е_а, η =1,0; l₀ = 6,0 м.

Вычисляем гибкость элемента λ = l₀ / h = 600/40 = 15 < 20.

По таблице 8 приложения при N_l / N = 900/1800 = 0,5 и l₀ / h =15 находятся коэффициенты φ_b = 0,84 и φ_sb = 0,875.

Принимаем μ + μ´= 1,0% и находим коэффициент α_s

α_s=R_sс μ/ R_b=355·10³ ·0,01/11, 5·10³ = 0,309.

Уточняется значение φ

φ= φ_b + 2(φ_sb – φ_b) α_s= 0,84 + 2(0,875 – 0,84)0,309 = 0,861.

Находится суммарная площадь арматуры

А_s+А´_s= (N/φ·R_sс) – (bhR_b /R_sс) =(1800/0,861·355·10³ ) - (0,4·0,4·11,5·10³ /355·10³) = 0,000706м² = 7,06см.²

Коэффициент армирования μ + μ´= 14,12 / 40·40 = 0,00883

μ + μ´= 0,00883 больше μ _min + μ´ _min = 0,001.

Уточнения площади арматуры не требуется, поскольку полученное значение 0,00883 не отличается существенно от заданного.

Окончательно, принимаем арматуру

4Ø16 А400, А_s + А´_s = 8,04 см².

Схема армирования сечения представлена на рис. 6.1.

Пример 6.2.Определить количество арматуры при следующих данных.

Колонна связевого каркаса с размерами b×h= 40×40 см. Бетон тяжелый В20, R_b =11,5 МПа, (11,5·10³ кН/м²), Е_в = 27,5·10³ МПа (27,5·10⁶кН/м²); рабочая арматура класса А400, R_s = R_sс = 355 МПа, (355·10³ кН / м² ), E_s= 2·10⁵ МПа (2·10⁸ кН/м²). Высота этажа 3,2м, защитный слой а = а´= 4 см, расчетная длина колонны равна высоте этажа l₀ = 3,2м.

В расчетном сечении действуют усилия только от вертикальных нагрузок.

От постоянных, длительных и временных вертикальных нагрузок продольная сила N_V= 400кН, момент M_v= 100кНм.

От постоянных и длительных вертикальных нагрузок продольная сила N_l= 300 кН, момент M_l= 50кНм.

Рабочая высота сечения

h_o = h – а= 40 – 4=36см = 0,36 м.

Определяем отношение l₀/h = 3,2 /0,4 = 8 > 4, обязателен учет гибкости.

Вычисляется жесткость элемента D при учете полных нагрузок, т.е.

М = 100кНм, N = 400 кН.

Эксцентриситет е₀ = M/N = 100/400 = 0,25м = 25,0 см.

e_a ≤ 10 мм; e_a ≤ h/30 = 40/30 = 1,33см; е_a ≤ l/600 = 3,2/600 = 0,53 см.

е₀ = 25,0 см > е_а = 1,33см;

Таким образом, изгибающий момент не уточняется.

М₁ = М + N(h₀ - a')/2 = 100 + 400(0,36 – 0,04)/2 = 164 кНм.

М_1l = М _l + N _l (h₀ - a') / 2 = 50 + 300(0,36 – 0,04)/2 = 98,0 кНм.

φ_l = 1+ М₁ / М_1l = 1+ 98,0/164 = 1,60 < 2,0.

δ_е = е₀ / h₀ = 25,0 /36 = 0,694 > 0,15. Принимаем δ_е = 0,694.

Коэффициент приведения арматуры к бетону

α = E_s /Е_в = 2·10⁵ / 27,5·10³ = 7,27.

Предварительно зададимся коэффициентом армирования μ = 0,015.

Вычисляем коэффициент μα. μα = 7,27·0,015 = 0,1091.

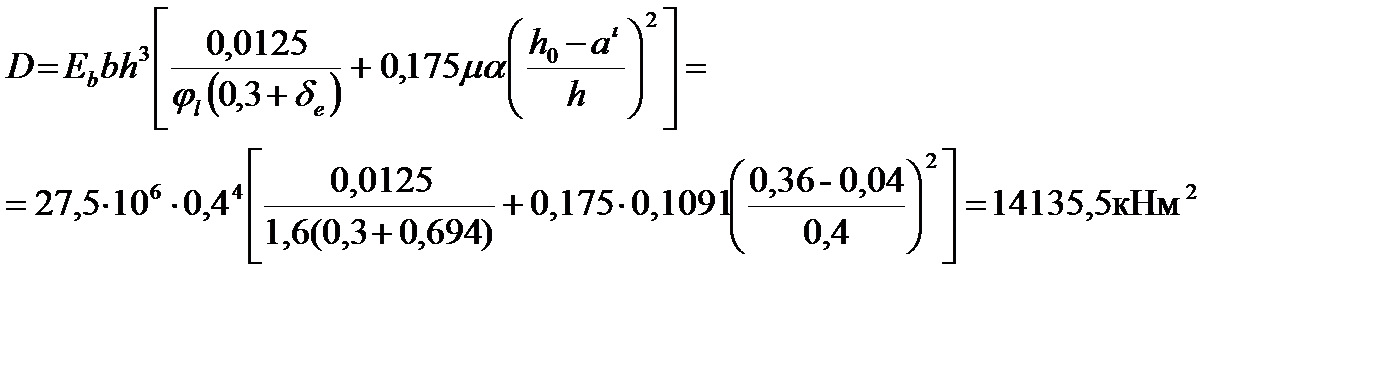
Находится величина критической силы

N_cr = π²D /l₀² = 3,14²·14135,5 / 3,2² = 13610,4 кН.

Коэффициент, учитывающий влияние прогибов колонны

η_v = 1/(1- N/N_cr) = 1/(1- 400/13610,4) =1,03.

Момент, с учетом влияния прогиба

М = M_v η_v = 100·1,03 = 103 кНм.

Для установления количества арматуры произведем промежуточные вычисления.

δ =a' / h₀ = 4 /36 = 0,111,

α_n = N / R_bbh₀ = 400/11,5·10³·0,4·0,36 = 0,242,

ξ_R = 0, 531; α_R = 0,390.

1 – 1

Рис.2.10. Армирование сжатого элемента к примеру 2.11. 1 – 2Ø14 А400 АS=3,08 см2, 2 – 1Ø12 А300 АS=1,131см2, 3 – 4Ø8 А240 АSW=2,01 см2.

Поскольку α_n = 0,242 < ξ_R = 0, 531, количество арматуры определяем по формуле

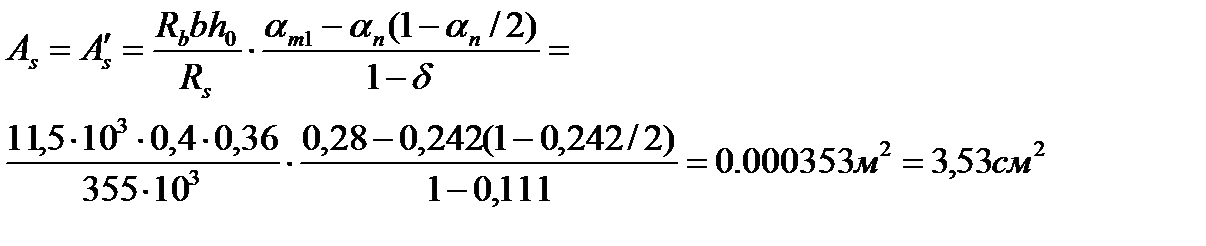
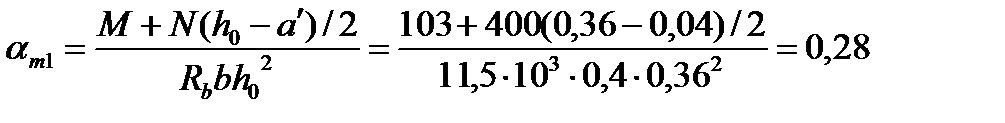Принимаем для армирования A_s = A'_s = 2Ø14 +1Ø12 А400 с общей площадью сечения арматуры 3,08 +1,131 = 4,211см². Схема армирования сечения представлена на рис. 6.2.

В соответствии с данными таблицы 6.1 выполнить расчет прочности сжатого со случайными эксцентриситетами элемента прямоугольного профиля. Определить требуемое количество продольной арматуры. Законструировать сечение с соблюдением конструктивных и нормативных требований. Выполнить чертежи армирования в масштабе 1:10 или 1:25.

Таблица 6.1

№	Расчетная продольная сила кН	Высота сечения h см	Ширина сечения b см	Класс бетона	Класс арматуры
Полная N	Длительная Nl
					В25	А400
					В25	А400
					В25	А400
					В25	А400
					В25	А400
					В25	А400
					В25	А400
					В30	А500
					В30	А500
					В30	А500
					В30	А500
					В30	А500
					В30	А500
					В30	А500
					В30	А400
					В30	А400
					В30	А400
					В30	А400
					В30	А400
					В30	А400
					В35	А400
					В35	А500
					В35	А500
					В35	А500
					В35	А500

В соответствии с данными таблицы 6.2 выполнить расчет прочности сжатого с расчетными эксцентриситетами элемента прямоугольного профиля. Определить требуемое количество продольной арматуры. Законструировать сечение с соблюдением конструктивных и нормативных требований. Выполнить чертежи армирования в масштабе 1:10 или 1:25.

Таблица 6.2

№	Расчетная продольная сила кН	Расчетный момент кНм	Высота сечения h см	Ширина сечения b см	Класс бетона	Класс арматуры
Полная N	Длит. Nl	Полный М	Длит. Мl
							В25	А400
							В25	А400
							В25	А400
							В25	А400
							В25	А400
							В25	А400
							В25	А400
							В30	А500
							В30	А500
							В30	А500
							В30	А500
							В30	А500
							В30	А500
							В30	А500
							В30	А400
							В30	А400
							В30	А400
							В30	А400
							В30	А400
							В30	А400
							В35	А400
							В35	А500
							В35	А500
							В35	А500
							В35	А500

Контрольные вопросы

1. Назовите классы тяжелого бетона на сжатие.

2. Назовите классы стержневой арматуры.

3. Какую часть от полной полезной нагрузки принимают как длительно-действующую.

4. Какую часть от полной снеговой нагрузки принимают как длительно-действующую.

5. В каких случаях сечение рассчитывается с двойной арматурой.

6. При расчете прочности ЖБЭ какие нагрузки используются: расчетные или нормативные?

7. При расчете прочности ЖБЭ какие характеристики бетона и арматуры используются: расчетные или нормативные?

8. Какие нагрузки больше расчетные или нормативные?

9. Какие характеристики бетона и арматуры больше: расчетные или нормативные?

10. Особенности разрушения изгибаемых элементов по нормальным сечениям. Граничное значение относительной высоты сжатой зоны сечений железобетонного элемента.

11. Проверка прочности о нормальным сечениям изгибаемых элементов прямоугольного профиля с одиночной арматурой. Подбор арматуры.

12. Подбор арматуры в изгибаемых элементах прямоугольного сечения по таблицам. Понятие о минимальном проценте армирования.

13. Проверка прочности по нормальным сечениям изгибаемых элементов прямоугольного профиля с двойной арматурой. Подбор арматуры.

14. Проверка прочности по нормальным сечениям изгибаемых элементов таврового сечения.

15. Подбор арматуры в изгибаемых элементах таврового сечения

16. Схемы разрушения изгибаемых элементов по наклонным сечениям. Расчет прочности по наклонным сечениям при действии изгибающего момента.

17. Расчет прочности изгибаемых элементов по наклонным сечениям при действии поперечной силы.

18. Особенности разрушения сжатых железобетонных элементов.

19. Прочность нормальных сечений внецентренно сжатых элементов и подбор арматуры.

20. Расчет прочности условно центрально сжатых элементов.

21. Учет случайных и расчетных эксцентриситетов.

22. Особенности расчета гибких сжатых элементов.

23. Расчет прочности центрально и внецентренно растянутых железобетонных конструкций.

24. Конструктивные требования по армированию изгибаемых и сжатых ЖБЭ.

Литература

Основная

1. Кузнецов В.С. Железобетонные и каменные конструкции. Учебник. АСВ, М.2015.

2. СП 20. 13330.2011 Свод правил. «Нагрузки и воздействия». Актуализированная версия к СНиП 2.01.07.85. М..,2011.

3. СП 52-01-2003. Бетонные и железобетонные конструкции. Основные положения. Актуализированная версия. М., 2012.

4. Кузнецов В.С. "Железобетонные конструкции многоэтажных зданий", М., АСВ, 2010.

Дополнительная

1. Байков В.Н., Сигалов Э.Е. “Железобетонные конструкции”, Общий курс, М., Стройиздат, 1991.

2. ГОСТ 10180-90. Бетоны. Методы определения прочности по контрольным образцам. М., 1990.

3. Кузнецов В.С., Малахова А.Н. "Железобетонные монолитные перекрытия и каменные конструкции многоэтажных зданий", М., АСВ, 2009.