Лекция № 15 (12.05.12)

(7,4) – коды

7 – кодовые разряды

4 – информационные «полезные» разряды

7-4 – контрольные разряды кода (n-k)

S – информационные разряды (кодируемый набор), контрольные разряды.

Свойства:

1. Разделимость (разделимый код) – у него есть специальные контрольные разряды, содержимое которых определяется информационными разрядами.

Не все коды обладают этим свойством. Например:

Наборы с 1 по n – ( ) – кодовые наборы. Это код неразделимый, все разряды эквивалентны. Это код систематический. На входе преобразователей мы формируем то значение, которое требуется реализовать. Такие коды называют кодами с повторениями.

Надежность характеризуется матрицей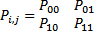

2. Систематичность – все составляющие набора попадают в набор не измененными.

Скорость передачи:

Она должна стремиться к 1.

Этап декодирования:

Описать трансформацию кодового набора типа 0110 110 -> 0110 111, где в последней составляющей произошла ошибка.

Корректирующая способность кода оценивается кратностью исправляемых ошибок.

Код с такой метрикой позволяет обнаружить и исправить все однократные ошибки. Ошибки с четной кратностью не обнаруживаются.

, где t – кратность.

Н – транспонированная матрица

Декодирование заключается в том, что мы берем – синдром.

Вывод: если Е=0, то . Признак безошибочного срабатывания является нулевое значение синдрома. – мощность множества значений синдрома должна быть больше или равна n+1. потому что, у нас, во-первых, должно быть n комбинаций синдрома для того, чтобы описать все позиции, где может произойти ошибка, а 1 – это когда синдром равен нулю, т.е. ошибки нет.

Синдром говорит нам о том, что ошибка состоялась и о месте (позиции), в котором она состоялась.

Синдром – это n-k – вектор столбец.

– алгебраическая интерпретация синдрома.

Пример:

– возникла ошибка.

E= 0000001.

– на первую строку матрицы H.

– на вторую строку матрицы H.

1 – на третью строку матрицы H.

Получили синдром. Он не равен 0. Ошибка в 3 разряде.

Мы можем закодировать комбинаций.