Косвенные измерения
Косвенные измерения предполагают наличие функциональной связи Y = f(x1, x2, . . . , xm), где х – подлежащие прямым измерениям аргументы функции Y или Q = F(Q1, Q2, … Qm). Погрешности при оценке Y, Q будет зависеть от погрешностей при измерениях аргументов. Функциональная зависимость может быть линейной и нелинейной.
Линейная ФЗ самая простая форма связи между измеряемой величиной и находимыми аргументами выражается зависимостью:
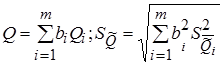
где bi – постоянный коэффициент влияния аргумента Qi на функцию Q, m - число аргументов. СКО результата измерения SQ.
Доверительные границы случайной погрешности результата косвенного измерения могут быть рассчитаны по формулам: 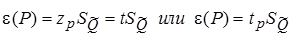
Доверительные границы неисключенной СИП результата косвенного измерения, если заданы границы ± qi или доверительные границы ± qi (Рj) могут быть рассчитаны по формулам:
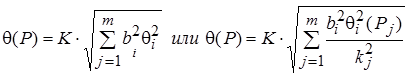
Значения коэффициента k определяется по табл. в зависимости от доверительной вероятности и числа суммируемых слагаемых (m), изменяется в пределах 0,95 ¸1,4 .
Значения систематических и случайных составляющих погрешности используют для оценки погрешности результата косвенных измерений. В зависимости от отношения неисключенной СИП и оценки СКО результат измерения записывается:
| Значение отношения q/SQ | Результат измерения |
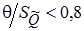 | Хи ± e (Р) |
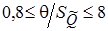 | Хи ± kp [e (Р) + q (P)] |
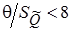 | Хи ± q (Р) |
Kp – определяется по табл. в зависимости от вероятности и значения соотношения, изменяется в пределах: 0,7 ¸ 0,85.
Нелинейная ФЗ при обработке используется метод линеаризации, состоящий в том, что функция связывающая измеряемую величину с аргументом раскладывается в ряд Тейлора. 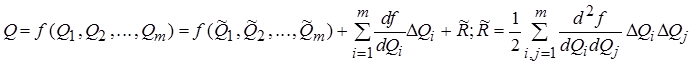
Где 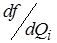 - первая частная производная от функции f по аргументу Qi, вычисленная в точке
- первая частная производная от функции f по аргументу Qi, вычисленная в точке 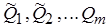 ; DQi – отклонение результата измерения аргумента Qi от его СКО; R – остаточный член, которым при использовании этого метода пренебрегают.
; DQi – отклонение результата измерения аргумента Qi от его СКО; R – остаточный член, которым при использовании этого метода пренебрегают.
Оценка результата определяется по формуле: 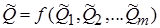 ,
,
где Qi – оценка результата измерений аргумента Qi, получаемая посредством обработки результатов многократных измерений каждого из аргументов. Абсолютная погрешность косвенного измерения D = Q - Q.
Разобранные выше методы используются в случае отсутствия корреляционной связи между аргументами. Корреляция в переводе с латинского - соотношение. Корреляция в математической статистике – вероятностная или статистическая зависимость. Корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов.
При наличии корреляционной связи между погрешностями измерений аргумента используется метод приведения. Он предполагает наличие ряда согласованных измерений аргументов:
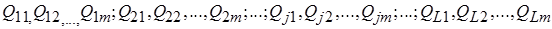 , полученных в процессе многократных измерений.
, полученных в процессе многократных измерений.
Результат косвенного измерения Q и СКО его случайной погрешности, доверительный интервал вычисляются по формулам:
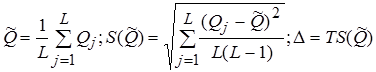
Т – коэффициент, зависящий от вида распределения и доверительной вероятности.
