Специальные булевы функции

Рассмотрим следующие специальные булевы функции, на основе которых могут быть построены другие:

0, 1 – константы, могут рассматриваться как булевы функции от любого числа

переменных ;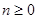

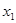– тождественная функция (или проекция );

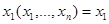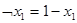– отрицание, обозначается также ;

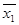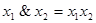– конъюнкция;

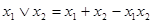– дизъюнкция;

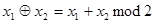– сложение по модулю 2;

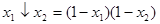– стрелка Пирса;

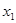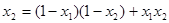~ – эквивалентность;

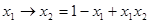– импликация;

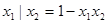– штрих Шеффера.

Эти функции можно определить с помощью таблиц истинности:

x1	x2	&	Ú	Å	¯	~	®	|	Ø

Реализация функций формулами

Пусть – множество булевых функций. Понятие формулы над F определяется индуктивно:

1. Каждая переменная 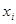и каждая булева функция из F являются формулами над F.

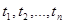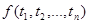2. Если – формулы над F, то для каждой функции из F выражение вида являются формулой над F.

Каждой формуле над F соответствует булева функция, которая называется интерпретацией этой формулы. Интерпретацию, как и формулу, можно определить индуктивно:

1. Интерпретация формулы 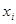сопоставляет элементу 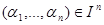элемент .

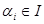2. Интерпретация формулы 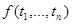принимает значения 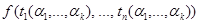, где функции 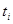дополняются, в случае необходимости, фиктивными переменными.

Пример

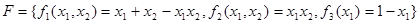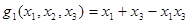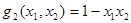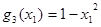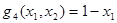Пусть . Тогда , , и – формулы над F, ибо

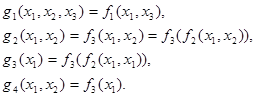
Подставляя 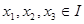в формулы, получим значения интерпретаций этих формул.

Если интерпретацией формулы g является булева функция f, то формула g называется реализацией функции f. Две формулы называются равносильными, если их интерпретации равны.

Например, формулы 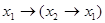и 1, над 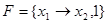, равносильны, ибо функция 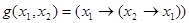принимает значения 1, для всех .

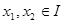Множество классов равносильных формул составляют булеву алгебру относительно операций:

& , Ú , Ø,

которая называется алгеброй Линденбаума – Тарского.

В следующем разделе будет доказано, что все булевы функции реализуемы формулами над 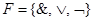, поэтому классы равных булевых функций можно рассматривать как элементы этой булевой алгебры.

Совершенная дизъюнктивная нормальная форма

Теорема. Каждая булева функция 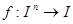реализуема с помощью формулы над .

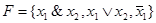Доказательство. Функция 0 реализуема с помощью формулы: 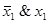. В общем случае имеет место равенство: 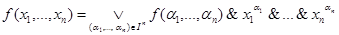, где 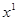обозначает , а 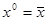. Здесь обозначает логическую сумму всех значений функции 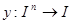. Это приводит к равенству, доказывающему теорему: .

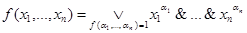Правая часть этого равенства называется совершенной дизъюнктивной нормальной формой (СДНФ).

Пример 1

Найдем СДНФ для функции 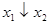. С этой целью составим таблицу истинности:

x1	x2	x1¯ x2

Поскольку лишь на элементе 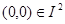значение функции 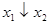равно 1, то .

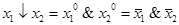Конъюнктивная нормальная форма определяется как конъюнкция формул вида: 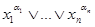. В силу равенств 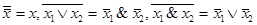получаем соотношение:

.

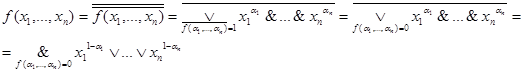Это представление функции f называется ее совершенной конъюнктивной нормальной формой (СКНФ).

Пример 2

Найдем СКНФ функции . Составим таблицу истинности:

x1	x2	x1® x2

Так как 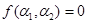лишь в случае 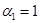и 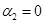, то СКНФ будет равна: 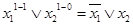. Заметим, что СКНФ формулы 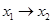будет равна: 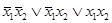. Система булевых функций F называется полной, если каждая булева функция реализуема с помощью формулы над F. Поскольку 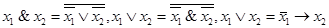, то имеет место следствие.

Следствие. Системы функций 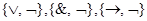являются полными.