Тема I.3. Равносильность формул. Законы логики высказываний. 1.3.1.Используя таблицы истинности, доказать эквивалентность следующих пар формул:
1.3.1.Используя таблицы истинности, доказать эквивалентность следующих пар формул:
а) 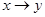 и
и 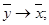
б) 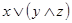 и
и 
в) 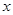 и
и 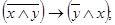
г) 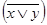 и
и 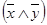
1.3.2.Построите такую формулу логики высказываний  чтобы …
чтобы …
а) формула 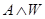 была равносильна формуле
была равносильна формуле 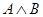 , а формула
, а формула 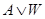 - формуле
- формуле 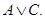 Ответ обосновать;
Ответ обосновать;
б) формула 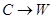 была равносильна формуле
была равносильна формуле 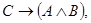 а формула
а формула 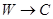 - формуле
- формуле 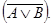 Ответ обосновать.
Ответ обосновать.
1.3.3.Психолог Сидоренко прошел три разных тестирования по определению типологии личности. Первое предполагало выявление двух признаков: «интуит», «этик»; второе было связано с проверкой признаков «сенсорик», «иррационал»; третье – выявление признаков «логик», «рационал».
Эксперимент заключался в том, что Сидоренко умышленно в каждом тесте по одному из признаков давал ложную информацию о себе. В результате каждый тест дал положительный ответ относительно соответствующих признаков.
Нужно выяснить, какое заключение можно сделать о характерных для Сидоренко признаках на основе полученных результатов и возможно ли при этом истинная характеристика?
1.3.4.В результате тестирования были выявлены следующие факты:
1) если Анохин не является экстравертом, то либо Венухин является экстравером, либо Селянин, причем не оба одновременно;
2) если Венухин не является экстравертом, то Анохин экстраверт, а Селянин – нет;
3) если Анохин экстраверт, то и Венухин экстраверт. Выяснить, кто согласно указанным утверждениям является экстравертом.
1.3.5.Три свидетеля ограбления банка дали показания. Первый свидетель заявил, что грабители скрылись на автомобиле зеленого цвета марки «Жигули». Второй свидетель утверждал, что это была черная «Волга». Третий свидетель настаивал на «Москвиче» не темного цвета.
Как выяснилось позже, каждый свидетель был лицом заинтересованным и поэтому указал правильно либо только марку машины, либо её цвет. Какого цвета был автомобиль и какой марки?
Тема I.4. Аксиоматический метод. Исчисление высказываний.
1.4.1.Пусть 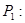 « Я сдам экзамен или поеду в Крым»;
« Я сдам экзамен или поеду в Крым»;
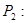 « Если я сдам экзамен, то поеду в Крым».
« Если я сдам экзамен, то поеду в Крым».
Выяснить, имеет ли место следование 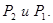
1.4.2.Известно, что если Джонс не встречал этой ночью Смита, то Смит – убийца. Джонс говорит неправду, или Смит не убийца. Джонс говорит правду. Верно ли, что Джонс встретил ночью Смита?
1.4.3.Выяснить, имеют ли место следования:
а)  б)
б) 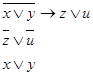
1.4.4.Доказать с помощью метода резолюций или опровергнуть с помощью таблицы истинности:
Верно ли, что из 1) 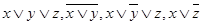
логически следует: а) x; б) y; в) z.
2) 
логически следует: а) x; б) y; в) z.
Тема I.5. Нормальные формы формул логики высказываний.
1.5.1.Привести к д.н.ф. формулу 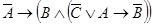
1.5.2.Привести к к.н.ф. формулу 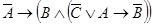
1.5.3.Упростить формулу 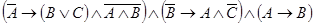
Раздел II. Основные структуры.
Тема II.1; II.2; II.3. Понятие булевой функции. Равенство функций.
