Правила построения формул логики высказываний
1. Элементарное высказывание (буква) является формулой нулевого уровня. Если элементарное логическое высказывание всегда верно, мы будем его обозначать буквой И, а если оно всегда неверно, — буквой Л. Тогда формулы первого уровня — это элементарные высказывания, к которым применена только одна логическая связка.
2. Пусть Ф1 и Ф2 — формулы ненулевого уровня. Тогда записи ((Ф1)), ((Ф1) 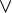 (Ф2)), ((Ф1)
(Ф2)), ((Ф1) 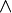 (Ф2)), ((Ф1)→(Ф2)) также являются формулами. Если же одна из формул Ф1 и Ф2 , к которым применяется логическая связка, имеет нулевой уровень, то она в скобки не заключается.
(Ф2)), ((Ф1)→(Ф2)) также являются формулами. Если же одна из формул Ф1 и Ф2 , к которым применяется логическая связка, имеет нулевой уровень, то она в скобки не заключается.
Теперь, зная буквы-элементарные высказывания, мы никогда не ошибёмся, определяя, является ли формулой запись, содержащая эти буквы, скобки и символы связок, то есть правильно ли построено сложное высказывание. В процессе подобного опознавания мы выделяем части формулы, то есть более короткие формулы, из которых на каждом этапе строится более длинная формула с применением одной связки. Самыми простыми частями формулы являются, разумеется, элементарные высказывания. Значит, логический анализ формулы сводится к выделению всех её частей.
Править]Пример
Пусть элементарными высказываниями являются А, В, С. Записи
A 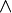 BC и (B)
BC и (B) 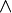 (B
(B 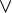 A→C)
A→C)
c формальной точки зрения не являются формулами, так как мы натыкаемся при их разборе на нарушение правил построения формул. (В первом случае отсутствует логическая связка между B и C и отсутствуют скобки вокруг A. Во втором случае формула нулевого уровня В включена в скобки). А записи
( A) 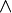 (B
(B 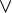 C) и B
C) и B 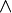 ((B
((B 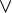 A)→C)
A)→C)
вполне соответствуют требованиям построения формулы. В процессе анализа формулы ( A) 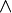 (B
(B 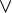 C) выделяются следующие её части:
C) выделяются следующие её части:
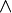 ( B
( B 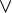 C )
C ) 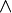 | Связующее действие A B
| Связующее действие A B 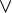 C | Разделённые части (формулы первого уровня)
C | Разделённые части (формулы первого уровня) 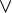 | Связующее действие A B C | Разделённые части (формулы нулевого уровня) | Все разделённые части являются элементарными высказываниями; разбор закончен.
| Связующее действие A B C | Разделённые части (формулы нулевого уровня) | Все разделённые части являются элементарными высказываниями; разбор закончен.Соглашения о скобках
Поскольку в построенных по определению формулах оказывается слишком много скобок, иногда и не обязательных для однозначного понимания формулы, математики приняли соглашения о скобках, по которым некоторые из скобок можно опускать. Записи с опущенными скобками восстанавливаются так:
§ Если опущены внешние скобки, то они восстанавливаются.
§ Если рядом стоят две конъюнкции или дизъюнкции (например, 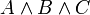 ), то в скобки заключается сначала самая левая часть (т.е. две подформулы со связкой между ними). (Говорят также, что эти связки левоассоциативны.)
), то в скобки заключается сначала самая левая часть (т.е. две подформулы со связкой между ними). (Говорят также, что эти связки левоассоциативны.)
§ Если рядом стоят разные связки, то скобки расставляются согласно приоритетам: 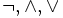 и
и 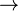 (от высшего к низшему).
(от высшего к низшему).
Когда говорят о длине формулы, имеют в виду длину подразумеваемой (восстанавливаемой) формулы, а не сокращённой записи.
Например: запись 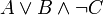 означает формулу
означает формулу 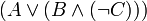 , а её длина равна 12.
, а её длина равна 12.
Истинностное значение
Интерпретацией (моделью) языка логики высказываний называется функция из множества всех пропозициональных переменных в множество истинностных значений {0, 1}. Основной задачей логики высказываний является установление истинностного значения формулы, если даны истинностные значения входящих в неё переменных. Истинностное значение формулы в таком случае определяется индуктивно (с шагами, которые использовались при построении формулы) с использованием таблиц истинности связок[3].
Оценка отрицания 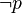 задаётся таблицей:
задаётся таблицей:
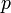 | 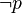 |
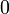 | 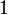 |
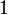 | 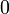 |
Значение двуместных логических связок 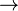 (импликация),
(импликация), 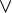 (дизъюнкция) и
(дизъюнкция) и 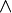 (конъюнкция) определяются так:
(конъюнкция) определяются так:
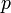 | 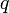 | 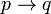 | 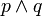 | 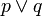 |
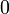 | 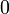 | 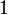 | 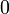 | 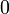 |
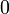 | 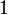 | 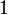 | 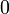 | 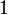 |
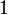 | 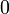 | 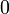 | 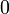 | 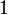 |
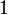 | 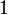 | 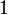 | 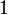 | 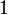 |
Тождественно истинные формулы (тавтологии)
Формула является тождественно истинной, если она истинна при любых значениях входящих в неё переменных (то есть, при любой интерпретации)[4]. Вот несколько широко известных примеров тождественно истинных формул логики высказываний:
Законы де Моргана:
1) 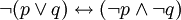 ;
;
2) 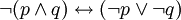 ;
;
Закон контрапозиции:
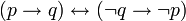 ;
;
Законы поглощения:
1) 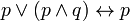 ;
;
2) 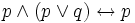 ;
;
Законы дистрибутивности:
1) 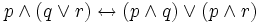 ;
;
2) 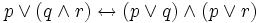 .
.
Исчисление высказываний
Одним из возможных вариантов (Гильбертовской) аксиоматизации логики высказываний является следующая система аксиом:
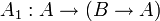 ;
;
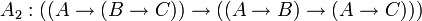 ;
;
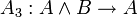 ;
;
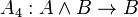 ;
;
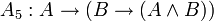 ;
;
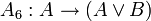 ;
;
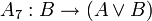 ;
;
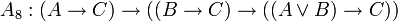 ;
;
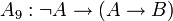 ;
;
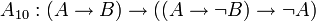 ;
;
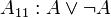 .
.
вместе с единственным правилом:
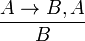 (Modus ponens)
(Modus ponens)
Теорема корректности исчисления высказываний утверждает, что все перечисленные выше аксиомы являются тавтологиями, а с помощью правила modus ponens из истинных высказываний можно получить только истинные. Доказательство этой теоремы тривиально и сводится к непосредственной проверке. Куда более интересен тот факт, что все остальные тавтологии можно получить из аксиом с помощью правила вывода — это так называемая теорема полноты логики высказываний.
Понятие
Всякое понятие имеет содержание и объем. Содержанием понятия называется совокупность существенных признаков одноэлементного класса или класса однородных предметов, отраженных в этом понятии. Содержанием понятия «ромб» является совокупность двух существенных признаков: «быть параллелограммом» и «иметь равные стороны».
Объемом понятия называют класс обобщаемых в нем предметов. Объективно, т.е. вне сознания человека, существуют различные предметы, например животные. Под объемом понятия «животное» подразумевается множество всех животных, которые существуют сейчас, существовали ранее и будут существовать в будущем. Класс (или множество) состоит из отдельных объектов, которые называются его элементами. В зависимости от их числа множества делятся на конечные и бесконечные. Например, множество планет Солнечной системы конечно, а множество натуральных чисел бесконечно. Множество (класс) А называется подмножеством (подклассом) множества (класса) В, если каждый элемент А является элементом В. Такое отношение между подмножеством А и множеством В называется отношением включения класса А в класс В и записывается так: Это отношение вида и рода (например, класс «ель» входит в класс «дерево»).
Отношение принадлежности элемента а классу А записывается так: (например, а — «Байкал» и А — «озеро»).
Классы А и В являются тождественными (совпадающими), если А V В и В V А, что записывается как Закон обратного отношения между объемами и содержаниями понятий
В этом законе речь идет о понятиях, находящихся в родовидовых отношениях. Объем одного понятия может входить в объем другого понятия и составлять при этом лишь его часть. Например, объем понятия «моторная лодка» целиком входит в объем другого, более широкого по объему понятия «лодка» (составляет часть объема понятия «лодка»). При этом содержание первого понятия оказывается шире, богаче ( содержит больше признаков), чем содержание второго. На основе обобщения такого рода примеров можно сформулировать следующий закон: чем шире объем у первого из двух понятий , тем уже его (первого понятия ) содержание , и наоборот. Этот закон называется законом обратного отношения между объемами и содержаниями понятий . Он указывает на то, что чем меньше информация о предметах, заключенная в понятии , тем шире класс предметов и неопределеннее его состав (например, «растение»), и наоборот, чем больше информация в понятии (например, «съедобное растение» или «съедобное злаковое растение»), тем уже и определеннее круг предметов.
Итак, понятие -- это форма мышления, отражающая предметы в их существенных признаках.
Понятие -- одна из основных форм научного познания действительности. Формируя понятия, наука отражает в них изучаемые ею предметы, явления, процессы. Например, политическая экономия сформировала такие понятия, как «товар», «капитал», «стоимость»; правовые науки -- понятия «преступление», «наказание», «вина», «умысел», «правоспособность» и др.
