Предикаты. Кванторы. Формулы логики предикатов. Равносильность формул

Пусть М – некоторое множество. Если х принимает значения из М. То будем называть х предметной переменной, а множество М – областью определения переменной х. Если а – фиксированный элемент из М, то будем называть его предметной постоянной.

Определение. Одноместным предикатом Р(х), определённым на множестве М (двуместным предикатом Р(х,у), определённом на множествах М и Т) называется всякое предложение с предметной переменной х (переменными х и у), которое превращается в высказывание каждый раз когда переменная х (переменные х,у) заменяется фиксированным элементом (фиксированными элементами) из множества М (соответственно: из множеств М и Т, если при этом М = Т, то говорят, что предикат Р(х,у) определён на множестве М).

Аналогично можно дать определение трёхместного, четырёхместного и т. д. предикатов. Итак, предикат это не высказывание, это предложение (или, как ещё его называют – высказывательная форма) в котором есть пустые места обозначенные буквой х (буквами х,у) и лишь после подстановки вместо них элементов из М ( из М и Т) они превращаются в высказывания, которое является либо истинным, либо ложным, т. е. значение Р(а) предиката Р(х) при х = а является высказыванием. Итак, предикат при любом наборе значений входящих в него предметных переменных может принять только одно из двух значений: либо И либо Л.

Примеры. 1. Р(х): «х – простое число» - олноместный предикат, определённый на N.

Р(1) º « 1 – простое число» º Л; Р(2) º « 2 – простое число» º И; Р(4) º « 4 – простое число» º Л.

2. Q(х,y,z): «прямая х проходит через точки y и z» - трёхместный предикат, определённый на множествах П и М (П – множество прямых плоскости, М – множество точек плоскости; хÎП; у,zÎМ).

3. S(x,y): (х² + у² = 1) – двуместный предикат, определённый на R. S(1,0) º S(0,1) º ( 1² + 0² =1) º ( 0²+1² ) º И; S(0,0) º ( 0² + 0² = 0 ) º Л.

Некоторые часто встречающиеся предикаты имеют специальные обозначения. Например, «х меньше у»: х < y; « х является элементом множества R»: х Î Rи т. д.

Определение. Пусть Р(х) – предикат, определённый на множестве М. Областью истинности предиката Р называется множество тех значений х, при которых предикат Р принимает значение И и обозначается ОИр.

ОИ_р= {a / Р(а) º И}. Аналогично определяется ОИ_р для n-местных предикатов. Если Р(х) определён на R,то область истинности этого предиката удобно изображать на числовой прямой. Если же Р(х,у) определён на R –на координатной плоскости ХОУ.

Примеры. 1. Р(х): ( 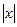< 1); ОИ_р= (-1,1): _{-1 О 1 Х}

2. Q(x,y): (x² + y² £ 4); ОИ_Q - круг с центром в точке О радиуса 2 :

У

2 Х

Так как предикаты принимают значения И и Л, то к ним применимы все логические операции алгебры высказываний. Если Р и Т предикаты, то Р&Т, РÚТ, РÞТ, РÛТ,`Р - тоже являются предикатами.