Перевод смешанного числа (целого и дробного) из десятичного счисления в другое счисление
Метод деления.
Представление десятичного числа в других системах счисления может проводиться по схеме Горнера. Допустим, что у нас есть целое число D, представленное с помощью основания системы счисления b, т.е. Dn. Процесс представления выполняется в несколько этапов по следующим правилам:
3 Последовательно делить заданное число и получаемые целые части на новое основание счисления до тех пор, пока целая часть не станет меньше основания нового счисления.
4 Полученные остатки от деления, представленные символами нового счисления, записать в виде числа, начиная с последней целой части.
Следовательно, на 1 этапе Dn = 
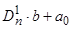, где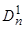 
- целая часть от деления, а0 – остаток. Этот остаток является первым младшим разрядом в новой системе счисления. На втором этапе деления получаем выражение вида
= 
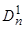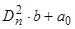и т.д.
Задача.
Представить по схеме Горнера десятичное число D10 = 147 в двоичном коде D2 = 10010011, в восьмеричном коде D8 =223, в шестнадцатеричном коде D16 = 93.
Проверить полученные результаты на инженерном калькуляторе.
Рассмотрим преобразование десятичных чисел в двоичные, восьмеричные или шестнадцатеричные на основе процедуры схемы Горнера, представленной в виде таблицы:
| Десятичное число D10 | Двоичное число D2 | Вес разряда |
| 13 : 2 = 6 с остатком 1 | ||
| 6 : 2 = 3 с остатком 0 | ||
| 3 : 2 = 1 с остатком 1 | ||
| 1 : 2 = 0 с остатком 1 |
| Десятичное число D10 | Двоичное число D2 | Вес разряда |
| 37 : 2 = 18 с остатком 1 | ||
| 18 : 2 = 9 с остатком 0 | ||
| 9 : 2 = 4 с остатком 1 | ||
| 4 : 2 = 2 с остатком 0 | ||
| 2 : 2 = 1 с остатком 0 | ||
| 1 : 2 = 0 с остатком 1 |
| Десятичное число D10 | Восьмеричное число D8 | Вес разряда |
| 271 : 8 = 33 с остатком 7 | ||
| 33 : 8 = 4 с остатком 1 | ||
| 4 : 8 = 0 с остатком 4 |
| Десятичное число D10 | D16 | Вес разряда |
| 27154 : 16 = 1697 с остатком 2 | ||
| 1697 : 16 = 106 с остатком 1 | ||
| 106 : 16 = 6 с остатком 10 | А | |
| 6 : 16 = 0 с остатком 6 |
| Десятичное число D10 | D16 | Вес разряда |
| 7589 : 16 = 474 с остатком 5 | ||
| 474 : 16 = 29 с остатком 10 | А | |
| 29 : 16 = 1 с остатком 13 | D | |
| 1 : 16 = 0 с остатком 1 |
Задача.
Самостоятельно записать процедуру перевода D10 =156 в D8 и на основе анализа процедуры преобразования чисел из одной системы счисления (D10) в другую D2, D8, D16 разработать алгоритм этой процедуры.
Решение:
| Десятичное число D10 | Двоичное число D2 | Вес разряда |
| 156:2 = 78 с остатком 0 | ||
| 78:2 = 39 с остатком 0 | ||
| 39:2 = 19 с остатком 1 | ||
| 19:2 = 9 с остатком 1 | ||
| 9:2 = 4 с остатком 1 | ||
| 4:2 = 2 с остатком 0 | ||
| 2:2 = 1 с остатком 0 | ||
| 1:2 = 0 с остатком 1 |
| Десятичное число D10 | Восьмеричное число D8 | Вес разряда |
| 156:8 = 19 с остатком 4 | ||
| 19:8 = 2 с остатком 3 | ||
| 2:8 = 0 остатком 2 |
| Десятичное число D10 | D16 | Вес разряда |
| 156:16 = 9 с остатком 12 | С | |
| 9:16 = 0 с остатком 9 |
15610 = 100111008 = 2348 = 9С16
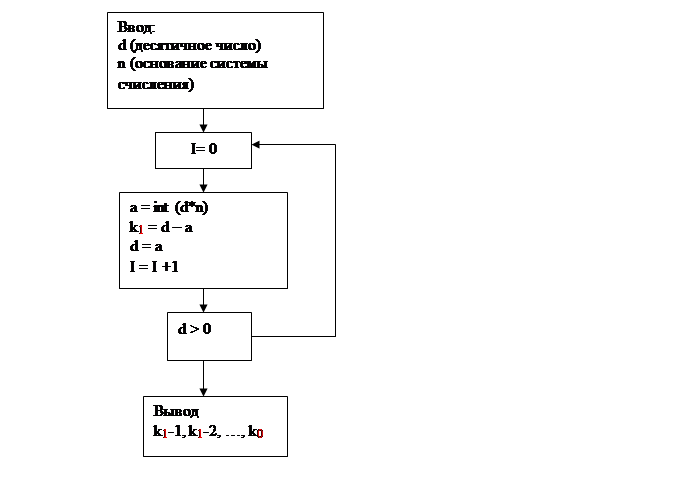
Алгоритм процедуры показан на рисунке:
Метод вычитания.
53 25 24 23 22 21 20
-32 ®25____ 1 1 0 1 0 1
-16 ®24____________
5____________________________
-4 ®22________________________________
-1 ®20_________________________________________
Метод умножения (Перевод дробного числа из десятичного счисления в другое счисление).
Правило:последовательно умножать данное число и получаемые дробные части произведений на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равна нулю или не будет получено требуемое по условию количество разрядов; полученные целые части являются разрядами числа в новой системе и их необходимо представлять цифрами этой новой системы счисления.
Пример.
Для преобразования десятичной дроби в двоичный эквивалент используем операцию последовательного умножения на 2. Если первое произведение окажется меньше 1, то запишем в старший разряд двоичной дроби 0. Если первое произведение ³ 1, то старшей цифрой двоичной дроби является 1. Аналогично определим вторую цифру двоичной дроби, причем на два умножается только дробная часть произведении, полученная на предыдущем шаге.
Задача.
0,6384×2=1,2768 ®1 0,4535×2=0,907 ®0
0,2768×2=0,5536 ®0 0,907×2=1,8140 ®1
0,5536×2=1,1072 ®1 0,8140×2=1,6280 ®1
0,1072×2=0,2144 ®0 2,6280×2=1,256 ®1
0,2144×2=0,04288®0 1,256×2=0,512 ®0
0,0×2=0,0 ®0 0,512×2=1,024 ®1
(0,6384)10 = (0,101000)2 0,024×2=0,048 ®0
0,048×2=0,096 ®0
0,096×2=0,182 ®0
(0,4535)10 = (0,011101000)2
Форматы чисел