Интенсивность отказов

На практике достаточно часто приходится определять 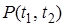-вероятность безотказной работы объекта в заданном интервале времени [t₁, t₂] , где t₁ < t₂ .

Эта вероятность является условной, поскольку безотказная работа объекта на отрезке времени [t₁, t₂] возможна только при условии, что на отрезке времени [0, t₁] объект был работоспособен.

Вероятность 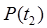- вероятность безотказной работы объекта на отрезке времени [0, t₂] - является вероятностью совместного появления двух зависимых событий: безотказной работы объекта на отрезке времени [0, t₁] и безотказной работы объекта на отрезке времени [t₁, t₂].

На основании формулы полной вероятности [2.1] запишем

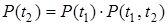, откуда

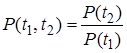. (2.10)

Определим теперь вероятность отказа объекта - Q (t₁, t₂) на отрезке времени [t₁, t₂] при условии, что на отрезке времени [0, t₁] объект был работоспособен.

Согласно (2.4), (2.10) .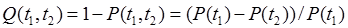

Допустим теперь, что 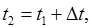где .

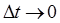Тогда .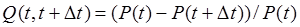

Поделим и умножим полученное выражение на .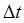

.

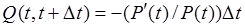Величина, равная 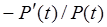, называется интенсивностью

отказов - .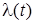

Интенсивность отказов 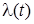- это условная плотность вероятности возникновения отказа объекта на бесконечно малом интервале времени [t, Δt], определяемая при условии, что до рассматриваемого момента времени t отказ не наступил.

Из определения следует, что

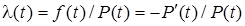. (2.11)

Интегрируя правую и левую часть выражения (2.11), а затем, избавляясь от логарифма в правой части, получим:

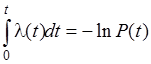или 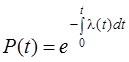. (2.12)

Выражение (2.12) показывает связь λ (t) и P(t): вероятность безотказной работы убывает экспоненциально в соответствие с интенсивностью отказов. По аналитически заданной функции λ (t) можно определить не только P(t), но и Т₁:

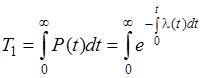. (2.13)

Статистическая оценка интенсивности отказов имеет вид:

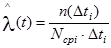, (2.14)

где 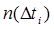- число отказов однотипных объектов на интервале 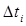, для которого определяется ;

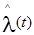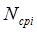- число работоспособных объектов в середине интервала .

,

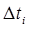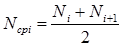где N_i - число работоспособных объектов в начале интервала ;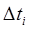
N_i+1- число работоспособных объектов в конце интервала .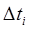

Если интервал 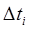уменьшается до нулевого значения 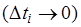, то

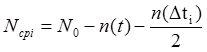, (2.15)

где N_о - количество объектов, поставленных на испытания;

∆t_i - интервал, продолжающий время t;

n( 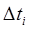) - количество отказов на интервале .

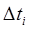Если для статистической оценки интенсивности отказов - λ (t) время эксперимента разбить на достаточно большое количество одинаковых интервалов Δt и провести наблюдения в течение длительного периода времени t , то результатом обработки опытных данных будет график, изображенный на рис. 2.2.

Как показывают многочисленные экспериментальные данные по анализу надежности технических объектов, в том числе и ЭВМ, линеаризованная обобщенная зависимость λ(t) представляет собой сложную кривую с тремя характерными интервалами (I, II, III). На интервале II (t₂ – t₁) λ(t) = const. Это - период нормальной эксплуатации объектов. Для электронных компонентов он может составлять десятки лет [2.1, 2.2, 2.3].

Интервал I (0, t₁) часто называют периодом приработки объектов. Он может увеличиваться или уменьшаться в зависимости от уровня организации производства на заводе-изготовителе, где элементы с внутренними дефектами своевременно изымаются из партии выпускаемой продукции. Величина интенсивности отказов на этом интервале во многом зависит от качества сборки схем сложных устройств, соблюдения требований монтажа и т.п. Включение под нагрузку собранных схем приводит к быстрому "выжиганию" дефектных элементов и по истечении некоторого времени t₁ в схеме остаются только исправные элементы, и их эксплуатация связана с λ (t) = const.

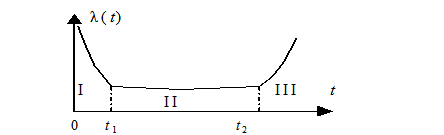
Рис. 2.2. Линеаризированная усредненная кривая жизни элемента:

I – интервал приработки; II – интервал нормальной эксплуатации; III – интервал старения

На интервале III (t > t₂) по причинам, обусловленным естественными процессами старения, изнашивания и т.д., интенсивность отказов резко возрастает, увеличивается число деградационных отказов.

Для того чтобы обеспечить λ(t) = const, необходимо заменить неремонтируемые элементы на исправные новые или работоспособные, отработавшие время t << t₂. Работа устройства на интервале времени, для которого λ(t) = const, может быть описана экспоненциальным законом распределения вероятности безотказной работы.Эта модель подробно проанализирована в подразделе 3.3. Здесь же отметим, что при λ(t) = const значительно упрощается расчет надежности, поэтому интенсивность отказов λ(t) наиболее часто используется как исходный показатель надежности элементной базы [2.1, 2.2, 2.3]. В заключение этого параграфа приведем сводную таблицу связи показателей безотказности невосстанавливаемых объектов ( табл. 2.1)

Таблица. 2.1

Связь между показателями безотказности

Базовые параметры	P(t)	Q(t)	f(t)	λ(t)	T1
P(t)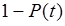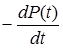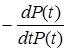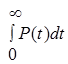
Q(t)	1-Q (t)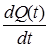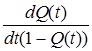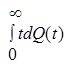
f(t)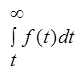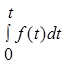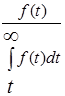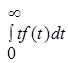
λ(t)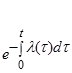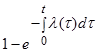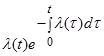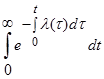