Аппроксимация функции ортогональными полиномами методом наименьших квадратов

(Подбор эмпирических зависимостей)

7.1. ОБЩИЕ ПОЛОЖЕНИЯ МЕТОДА

Автоматизация метрологических исследований требует определения и использования для математической обработки результатов измерения единых методов, удобных при работе с вычислительной техникой. Одной из ключевых проблем является представление результатов метрологических исследований с использованием ЭВМ, например, при совместных измеренияхдля определения зависимости между двумя или несколькими неодноименными величинами.

Из широкого круга задач рассматривается только наиболее часто встречающаяся задача аппроксимации, которая сводится к поиску аналитической зависимости в виде эмпирической формулы для случая, когда значения функции получены из наблюдения с некоторой погрешностью и представлены в табличной форме.

Одним из известных методов, применяемых для решения этой задачи, является метод наименьших квадратов (МНК) и его разновидность - аппроксимация функции ортогональными полиномами (МНКОП), которая была разработана Дж. Форсайтом [48, 55]. Одним из преимуществ данного метода является возможность автоматизации при выборе числа параметров функции (степени полинома), а также возможность дальнейшей автоматизации и использование других видов функций отличных от полиномов.

Указанный метод МНКОП рекомендуется также ИСО в ряде документов [Н15, Н16].

В данной главе мы изложим метод Форсайта, а также покажем как можно распространить данный метод на многомерный случай.

Искомое уравнение регрессии представляют в виде полинома [6 - 9, 12, 20, 21, 28, 29]

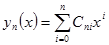(7.1)

где n - степень полинома; 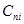- коэффициент полинома при i-ой степени аргумента x.

Мерой приближения выбранной зависимости к полученным экспериментальным значениям принимают сумму квадратов разностей экспериментальных значений 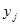и вычисленных значений регрессии 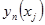в N узловых точках 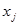, в связи с чем метод получил свое название метода наименьших квадратов.

При метрологических исследованиях результаты измерения могут быть получены с индивидуальной различной погрешностью, поэтому степень доверия к ним также различна. Математически это обстоятельство учитывается введением весовой функции

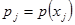(7.2)

которую обычно выбирают произвольно (см. ниже).

Таким образом, задачу сводят к выбору параметров (коэффициентов 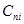полинома 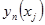), которые минимизируют функционал

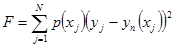(7.3)

где N - число точек наблюдения.

Аппроксимирующий полином 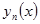можно также представить в виде линейной комбинации ортогональных полиномов [21, 26, 27, 53]

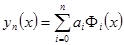(7.4)

где 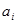- числовой коэффициент;

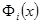- ортогональный полином i-ой степени с коэффициентом при старшем члене, равном единице.

Условие ортогональности записывают в виде

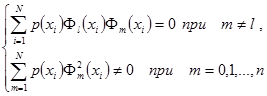(7.5)

Для нахождения коэффициентов 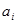при ортогональных полиномах подставляют в уравнение (7.3) выражение (7.4) и, приравнивая к нулю частные производные по 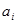, получают нормальную систему уравнений:

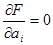(7.6)

где i = 0,1,...,n . Отсюда с учетом условий ортогональности получают

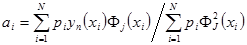(7.7)

где j = 0,1,...,n.

Для построения ортогональных полиномов принимают 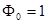, а остальные ортогональные полиномы ищут из уравнения

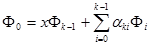(7.8)

где 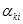- некоторый коэффициент.

Из условия ортогональности выражения (7.5) имеют число уравнений "k" для определения 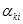, откуда

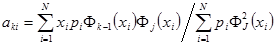(7.9)

Можно показать, что только два члена 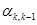и 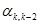, вычисленные по формуле (7.9) , будут не равны нулю.

Представив 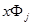в виде линейной комбинации ортогональных полиномов

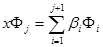(7.10)

и применив к произведениям, стоящим в числителе формулы (7.9),условие ортогональности , получают следующие выражения для коэффициентов:

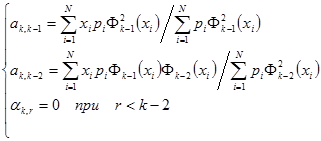(7.11)

Матрица коэффициентов 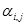ортогональных полиномов имеет вид

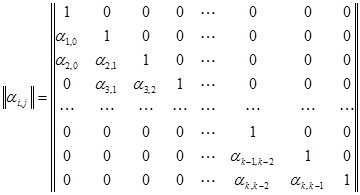
В результате получают следующие формулы для вычисления ортогональных полиномов:

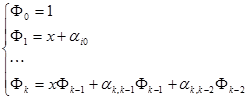(7.12)

Аппроксимирующий полином вычисляют по формуле (7.4) или по следующей формуле

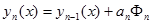(7.13)

Вычисление коэффициентов ортогональных и аппроксимирующего полиномов производится следующим образом.

Если расписать младшие ортогональные полиномы и привести подобные члены, то ортогональный полином k-й степени 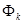будет иметь вид

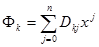(7.14)

где 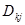- числовой коэффициент при j-й степени аргумента ортогонального полинома k-й степени.

Сравнивая выражения (7.12) и (7.14), можно получить следующие формулы для вычисления коэффициентов ортогональных полиномов:

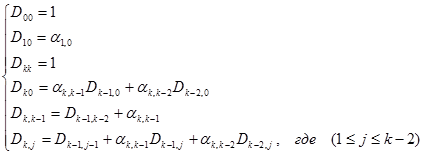
Матрицы коэффициентов ортогональных полиномов имеют треугольный вид с единицами по главной диагонали

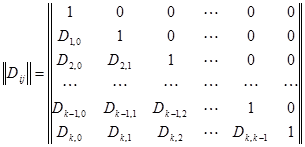
Коэффициенты аппроксимирующих полиномов вычисляют по формулам

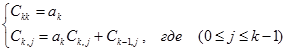
Матрица коэффициентов аппроксимирующего полинома также имеет треугольный вид с коэффициентами 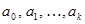по главной диагонали..

Построение функции регрессии с помощью описанного метода является основным, и он широко используется для решения различных метрологических задач [12].

Для реализации этого метода обычно составлены программы для ЭВМ, например подпрограмма OR [12]. Подпрограмма OR используется также при выборе эмпирических зависимостей для математического описания линии регрессии функциями отличными по своему виду от полиномов [10].