Отображение радиус – векторов

Пусть задана последовательность двумерных векторов 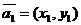, , 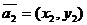…, 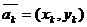. Требуется построить векторы в соответствии с законами векторной алгебры. Напомним, что координаты вектора, соответствуют координатам концов векторов, а начало всех векторов расположении в точке (0,0). Это графическое отображение осуществляет команда compass.

Пример 5.8. Построить векторы, соответствующие комплексным числам

z1=-1+2i; z2=-3i; z3=2+3i; z4=5+2i;

» z=[-1+2i,-2-3i,2+3i,5+2i];

» compass(z)

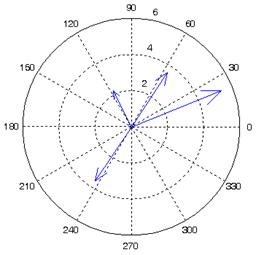
Рис.6. Векторы примера 5.8

5.7. Построение узлов разбиения прямоугольной области.

Пусть функция двух переменных z=f(x,y) задана в прямоугольной области a < x < b, c < y < d. Требуется построить узлы разбиения области (xi, yi) с шагом hx по x и шагом hy по y. Для этого MATLAB имеет команду meshgrid.

Для ее применения необходимо создать векторы x и y с заданными шагами hx и hy. Затем применить оператор [X,Y] = meshgrid(x, y), который создает два двумерных массива[X,Y]с координатами узлов.

5.8. Линии уровня функций двух переменных (горизонтальные сечения поверхности z=f(x,y))

Пусть задана функция z=f(x,y). Требуется построить линии уровня функции с заданным шагом. Предварительно необходимо построить сетку узлов, см.п.5.6 и вычислить значения функции в узлах: Z(xi,yj).

Команда contour(z) — строит линии постоянного уровня функции с автоматическим заданием диапазонов изменения х и у, равным текущим индексам i,j.

Команда contour(x,y,z) — строит линии уровня по данным матрицы z с указанием спецификаций для x и y; contour(z,n) и contour(x,y,z,n) — дает построения, аналогичные ранее описанным командам, с заданием n линий равного уровня (по умолчанию n=10);

Команда contour(z, v) и contour(x,y,z,v) — строят линии равного уровня для высот, указанных значениями элементов вектора v.

Команда contour(z,[v,v]) или contour(x,y,z,[v ,v]) — вычисляет одиночную линию уровня для заданного уровня v;

Команда contour('linespec') — позволяет использовать перечисленные выше команды с указанием способы отображения линий уровня.

Пример 5.9. Построить линии уровня (контурный график) поверхности, заданной функций peaks:

» z=peaks(27);

» contour(z,15)

Заметим, что объект — функция peaks — задан в системе в готовом виде.

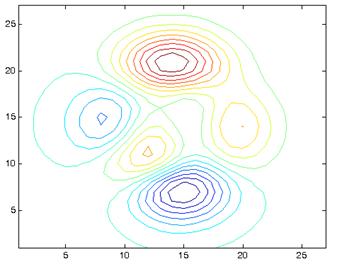
Рис.7. Линии уровня (контуры) графика поверхности

5.9. Изображение линий уровня в трёхмерном пространстве

Для функции z=f(x,y) линии уровня отображают в трехмерномпространстве с помощью команды contour3(Z).

Команда contour3(Z) строит линии уровня для массива данных (xi,yj,f(xi,yj)), определяющих поверхность в трехмерном пространстве без учета диапазона изменения координат x и y. Команда contour3(X, Y, Z), где X и Y - двумерные массивы, вычисленные с помощью функции meshgrid, рисует линии уровня для массива данных Z с учетом диапазона изменения координат x и y.

Команды contour3(Z, n), contour(X, Y, Z, n) рисуют n линий уровня для массива данных Z; по умолчанию n равно 10.

Функция C = contour3(...) возвращает массив C описания линий уровней по аналогии с функцией contourc для последующего использования командой clabel.

Функция [C, h] = contour3(...) возвращает массив C и вектор-столбец дескрипторов h графических объектов line для каждой линии уровня.

Пример 5.10. Построить линии уровня функции 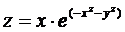в области -2 ≤ x ≤ 2, -2 ≤ y ≤ 3.

>>x = -2 : .2 : 2;
>>y = -2 : .2 : 2;
>>[X, Y] = meshgrid(x, y);
>>Z = X.* exp(- X.^2 - Y.^2);
>>contour3(X, Y, Z)

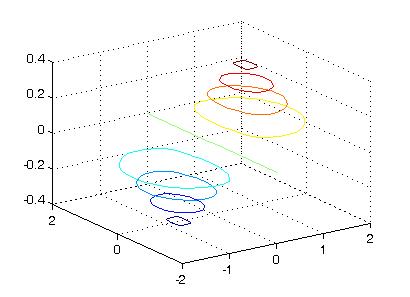
Рис.8. Трехмерные линии уровня

Замечание: При работе с командой и функцией contour3 предполагается, что элементы массивов x и y монотонно возрастают.