Пользуясь такими графиками , вы сможете решать тригонометрические уравнения и неравенства.
Ход урока
Организационный момент – 2 мин.
Проверка готовности учащихся к уроку, отметка отсутствующих, объявление темы и цели урока
Объяснение нового материала – 5 мин (Теоретическая часть)
На уроке рассмотрим функцию у = sin x на отрезке. Построим график и рассмотрим основные свойства функции.
Историческая справка: Понятие синуса имеет длительную историю. Уже в I I I веке до н.э. первоначально слово синус звучало как джива-тетива лука. Это слово было заменено на
латинское слово sinus -изгиб, кривизна. Слово косинус намного моложе. Косинус - это сокращенное латинское выражение «дополнительный синус».
Новая тема:
Запишем функцию у = sin x .
Основные свойства:
1.Область определения - множество R всех действительных чисел.
2.Множество значений - отрезок 
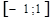
Этого достаточно чтобы построить график функции у = sin x.
Применение полученных знаний - 15 мин. (Практическая часть)
Сегодня мы рассмотрим применение табличного процессора Excel для графиков функций. Графики функций, так же как и диаграммы строятся с помощью Мастера диаграмм программы Excel.
Рассмотрим построение графиков функций на примере функции у = sin x.
Построить график функции у = sin x на отрезке [– 6; 6] с шагом h = 1.
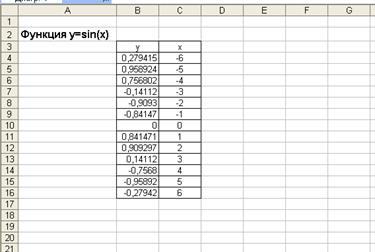
1. Заполним таблицу значений функции. В ячейку С4 введем первое значение отрезка: – 6, потом в C5 -5 и заполняем до C16, с помощью инструмента «автозаполнения» (Выбираем С4 и C5, нажимая и удерживая левую кнопку мыши выделяем до C15).
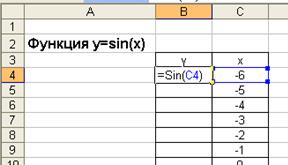 2. В ячейку B4 введем формулу, =Sin(C4), при этом формула будет ссылаться на ячейку C4, C4 примет как первое значение X.
2. В ячейку B4 введем формулу, =Sin(C4), при этом формула будет ссылаться на ячейку C4, C4 примет как первое значение X.
3. Далее используем снова инструмент «автозаполнения», но теперь уже в столбце с функцией Sin.
4.
1) Вызываем «Мастер диаграмм», которая находится в меню «Вставка» - «Диаграмма».
2) Выбираем в открывшемся диалоговом окне в вкладке «стандартные» - график, с левой панели крайний левый верхний график.
3) Добавляем новый ряд, Имя: y=sin(x), значение: =Лист1!$B$4:$B$15, подписи оси X: =Лист1!$C$4:$C$15
4) В заголовках пишем – y=sin(x), Ось X (категорий): Абсцисса, Ось Y (значений): Ордината. Вкладке «Линия сетки», убираем все галочки.
5.В полученном графике, 2 раза нажимая в линию оси X вызываем «Формат оси», в вкладке «Шкала» убираем все галочки и в окошке «Пересечение с осью Y» вставим 7.
6.2 раза нажимая в линию y=sin(x) взываем «Формат ряда данных», вставим галочку «Сглаженная линия» и по желанию меняем «Толщину»и «Цвет»
Остальные изменения выполняются аналогично.На самом деле пока это мало похоже на график функции в нашем привычном понимании.
Работа с раздаточными материалами – 5 мин. (Практическая часть)
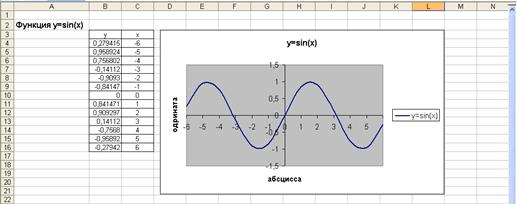
У вас получился график . (Учащимся выдается раздаточный материал с графиком).
Продолжим работу по графику.
1. Перейдем от чисел на абсциссе к радианной записи. Для этого воспользуемся таблицей, составленной на предыдущем уроке.
2. Отметим точки 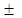 Пи,
Пи, 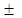 П/2,
П/2, 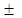 П/4,
П/4, 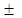 П/3,
П/3, 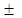 П/6,
П/6, 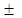 2П.
2П.
Вопрос классу: Почему мы выбираем эти значения??? (т.к. это табличные значения, которые часто используются при работе с тригонометрическими функциями)
Вернемся к записи свойств в тетради.
3.Функция у = sin x периодическая, с периодом 2П.
4. Функция у = sin x нечетная (sin (-x)= sin х) .
5. Функция у = sin x принимает :
-значение равное нулю, при х = Пп, п ЄZ;
-наибольшее значение, равное 1, при 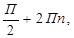 , п ЄZ ;
, п ЄZ ;
-наименьшее значение, равное -1, при - 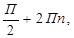 , п ЄZ ;
, п ЄZ ;
-положительные значения на интервале (0;П) и на интервалах, получаемых сдвигами этого интервала на 2Пп, п= 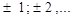 ;
;
-отрицательные значения на интервале (П;2П) и на интервалах, получаемых сдвигами этого интервала на 2Пп, п= 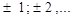
6. Функция у = sin x:
- возрастает на отрезке 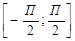 и на отрезках, получаемых сдвигами этого отрезка на 2Пп, п=
и на отрезках, получаемых сдвигами этого отрезка на 2Пп, п= 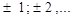 ;
;
- убывает на отрезке 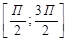 и на отрезках, получаемых сдвигами этого отрезка на 2Пп, п=
и на отрезках, получаемых сдвигами этого отрезка на 2Пп, п= 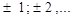 .
.
Пользуясь такими графиками , вы сможете решать тригонометрические уравнения и неравенства.
Самостоятельная работа. – 10 мин (Практическая часть)
Построить график функции у = sin(x)+2 на отрезке [– 6; 6] с шагом h = 1. Объяснить изменения графика на этом примере.
Подведение итогов.
-Что нового узнали на уроке?
-приведите примеры практического применения данной темы?
(Учитель показывает результат ЭКГ, как пример применения на практике)
От правильного прочтения кардиограммы зависит жизнь человека!!!
Домашнее задание.
Необходимо провести всю такую же работу с функцией y = cos(x).
Оценки за урок.
